深度学习的损失函数和反向传播涉及到很多数学知识,其原理解释在此。
1 似然估计
1.1 基本概念
似然估计贯穿于整个参数估计的过程,包含损失函数的定义、梯度的计算以及参数的更新。
- 定义:损失函数通常是似然函数,反映了模型预测的概率分布与真实数据分布之间的差异,定义这个损失函数是基于似然估计的原则。
- 梯度计算:在训练过程中,需要计算损失函数关于模型参数的梯度,这个梯度指示了参数空间中损失函数增加最快的方向。为了最小化损失函数,需要沿着梯度的反方向更新参数。计算梯度的过程也是基于似然估计的原则。
- 参数更新:在计算得到梯度后,使用优化算法(如梯度下降、Adam等)更新模型参数。这一步是似然估计的核心,通过更新参数来最小化损失函数。参数的更新是基于似然估计的目标。
1.2 最大似然估计
最大似然估计(Maximum Likelihood Estimation, MLE) 是统计学中的一种方法,用于估计概率模型中的参数。在给定数据 D = { x i , y i } i = 1 N D=\{x_i,y_i\}^N_{i=1} D={xi,yi}i=1N时,找到模型参数 θ \theta θ,使得数据出现的概率(似然)最大。
- 似然函数:似然函数是给定参数下观测数据的概率, L ( θ ) = ∏ i = 1 N P ( y i ∣ x i ; θ ) L(\theta)=\prod_{i=1}^NP(y_i|x_i;\theta) L(θ)=∏i=1NP(yi∣xi;θ)。对于离散随机变量,似然函数是概率质量函数(PMF)的乘积;对于连续随机变量,似然函数是概率密度函数(PDF)的乘积。
- 对数似然函数:为了简化计算,通常取似然函数的自然对数,得到对数似然函数, log L ( θ ) = ∑ i = 1 N log P ( y i ∣ x i ; θ ) \log L(\theta)=\sum_{i=1}^N \log P(y_i|x_i;\theta) logL(θ)=∑i=1NlogP(yi∣xi;θ)。
最大似然估计:最大似然估计是使似然函数或对数似然函数达到最大值的参数值。最大化对数似然等价于最小化负对数似然(Negative Log-Likelihood,NLL), J ( θ ) = − 1 N ∑ i = 1 N log P ( y i ∣ x i ; θ ) J(\theta)=-\frac{1}{N}\sum_{i=1}^N \log P(y_i|x_i;\theta) J(θ)=−N1∑i=1NlogP(yi∣xi;θ),这通常是深度学习中的交叉熵损失。
1.3 对数似然(Log-Likelihood)
基本原理——对数的加法运算法则: log a ( M N ) = log a ( M ) + log a ( N ) \log_a(MN)=\log_a(M)+\log_a(N) loga(MN)=loga(M)+loga(N)
直接对概率 P ( y ∣ x ; θ ) P(y|x;\theta) P(y∣x;θ)求导时,链式法则会导致复杂的计算(尤其是多层神经网络),对数梯度形式更易于计算。(建议再学习一下softmax概率交叉熵损失的梯度推导)
乘积形式的概率在计算时容易导致数值下溢,取对数可以将乘积转为求和,避免数值问题,同时对数函数的单调性保证最大化对数似然等价于最大化原始似然。
数值下溢(Underflow) 是计算机科学中一个常见的数值问题,指的是在计算过程中,某些数值变得非常小,以至于超出了计算机浮点数表示范围的下限,从而导致这些数值被近似为零的现象。
另外,对数转换后的梯度方差更小,有助于稳定训练。
2 正交子空间
2.1 正交向量(Orthogonal Vectors)
正交向量是指两个向量的内积(点积)为零。直观上,两个正交向量代表的几何意义是它们彼此垂直。
对于两个向量
u
u
u和
v
v
v,它们是正交的,当且仅当它们的内积为零:
u
⋅
v
=
0
u \cdot v = 0
u⋅v=0,其计算方式为
u
⋅
v
=
u
1
v
1
+
u
2
v
2
+
⋯
+
u
n
v
n
=
0
u⋅v=u_1v_1+u_2v_2 +⋯+u_nv_n=0
u⋅v=u1v1+u2v2+⋯+unvn=0。
正交向量的性质:
- 对称性:如果 u u u和 v v v正交,则 v v v和 u u u也正交。
- 零向量:任何向量与零向量都是正交的。
- 线性组合:如果向量 u u u和 v v v正交,那么它们的任意线性组合也会满足相同的正交条件。
2.2 子空间
子空间是线性代数中的一个基本概念,表示在一个更大空间内,符合线性结构的一个子集。换句话说,子空间是一个能够被线性运算封闭的向量集合。
一个集合 S S S是一个向量空间(或子空间),当且仅当满足以下三个条件:
- 零向量属于子空间:零向量必须属于集合 S S S。
- 加法封闭性:对任意的两个向量 u u u和 v v v,如果它们都属于子空间 S S S,则它们的和 u + v u+v u+v也必须属于 S S S。
- 数乘封闭性:对任意的向量 u u u和标量 c c c,如果 u u u属于子空间 S S S,则 c ∗ u c*u c∗u也必须属于 S S S。
如果线性空间 W W W的两个子空间 U U U和 V V V满足 v ∈ V , u ∈ U ⇒ v ⊥ u v\in V, u\in U \Rightarrow v⊥u v∈V,u∈U⇒v⊥u,那么就称这两个子空间是正交子空间,记作 U ⊥ V U⊥V U⊥V。
2.3 正交化
在一些应用中,我们需要从一个向量集合中找到正交基。这个过程叫做正交化。**格拉姆-施密特正交化(Gram-Schmidt Orthogonalization)**是一个常用的算法,它将一组线性无关的向量转化为一组正交向量。

每次构造正交向量时,第一步是计算在所有正交向量上的投影,第二步是减去它在所有之前正交向量上的投影,得到与之前向量都正交的新向量。(这里注意,n维空间中最多只能有n个线性无关的向量,尽管初始向量是线性无关的,但在正交化过程中,超出n个向量的部分将被正交化为零向量,因为它们在n维空间中无法保持线性无关。)
3 梯度计算和反向传播
使用gym内置的环境测试自己对DRL的理解和使用几乎没什么问题,但是如果应用到自己的问题,需要自定义环境、动作空间和状态空间,就会发现自己对DRL的理解还不是很透彻。尤其是在设计奖励时,突然想到一个问题:反向传播是如何进行的?以迷宫问题为例,输出的动作是离散的不可微分的,使用[0,1,2,3]表示(上/下/左/右)四个动作,奖励是在动作执行后由环境计算得出的,而非神经网络直接输出,和神经网络输出的动作的值之间并没有直接的联系,它们之间没有显式的公式。而据我所知,PyTorch反向传播依靠的是计算图,它可以保存神经网络输入到输出中间所有变量的关系传递,然后再通过计算图去反向传播。那对于这种情况,怎么去计算梯度呢?
Q&A
(1)动作和奖励的公式设计
首先需要明确:动作不需要显示体现在奖励的计算公式中。奖励函数的设计核心是衡量动作执行后环境的反馈,而动作的影响是通过环境状态的变化间接体现的。奖励是环境对智能体动作的评价信号,表示该动作的好坏,动作只是决定了状态如何转移,奖励是基于新状态的属性。所以策略学习的目标是通过调整概率,使得智能体更可能选择那些导致高奖励状态转移的动作。智能体应通过学习发现“哪些动作在哪些状态下更好”,通过奖励信号学习“状态-动作”映射关系,而非记忆动作的绝对好坏、被奖励函数硬性规定。
(2)梯度是如何计算的
策略梯度定理中计算的是期望累积奖励 J ( θ ) = ∇ θ log π θ ( a ∣ s ) R J(θ)=∇_θ\log{π_θ (a|s)}R J(θ)=∇θlogπθ(a∣s)R的梯度,不单单是每一步的奖励。
策略梯度算法直接对策略网络进行优化,通过计算动作概率来间接实现可微分。对于离散动作空间,策略可以表示为条件概率分布 π θ ( a ∣ s ) π_θ (a|s) πθ(a∣s),即参数为 θ θ θ的策略网络在状态 s s s下选择动作 a a a的概率。动作概率 π θ ( a ∣ s ) π_θ (a|s) πθ(a∣s)表示智能体对动作的偏好,对数概率 ∇ θ log π θ ( a ∣ s ) ∇_θ\log{π_θ (a|s)} ∇θlogπθ(a∣s)表示概率变化的方向,也就是梯度方向。奖励 R R R作为权重,告诉算法该动作的好坏,高奖励的动作梯度方向为正,增加其概率,低奖励的动作梯度方向为负,降低其概率。
比如智能体要考虑某一环境下是否抛硬币,抛为动作0,不抛为动作1,若正面朝上奖励+2,反面朝上奖励-2,不抛奖励不增不减,如果策略网络抛出硬币的概率为 p p p,不抛的概率为 ( 1 − p ) (1-p) (1−p),假设此时以概率 p p p抛了一枚硬币且正面朝上,那么概率梯度为 ∇ l o g p ∗ 2 ∇ logp*2 ∇logp∗2,表示希望增加 p p p的值,假设此时以概率 p p p抛了一枚硬币且反面朝上,那么梯度为 ∇ l o g p ∗ ( − 2 ) ∇ logp*(-2) ∇logp∗(−2),表示希望减少p的值。
(3)为什么对数概率能够表示概率变化的方向
设概率函数为
p
(
θ
)
p(θ)
p(θ),对数概率为
log
p
(
θ
)
\log{p(θ)}
logp(θ),其导数为
d
log
p
(
θ
)
d
θ
=
1
p
(
θ
)
⋅
d
p
(
θ
)
d
θ
\frac{d_{ \logp(θ)}}{d_θ} =\frac{1}{p(θ)}·\frac{d_{p(θ)}}{d_θ}
dθdlogp(θ)=p(θ)1⋅dθdp(θ),可见对数函数的符号和原概率函数的符号是相同的,在此基础上还表示了概率的相对变化率,即参数变化对概率的影响比例。使用对数函数的原因主要有以下几点:
(1)数值稳定性:对数函数将乘法转化为加法,避免概率连乘导致的数值下溢。
(2)数学简洁性:参考策略梯度定理。
(3)方向一致性:对数概率梯度与概率梯度方向相同,但更易计算和优化.
(4)从图像的角度理解梯度的计算
对数概率梯度相当于坡度,为正表示正在上坡,动作概率会增加,为负表示正在下坡,概率会减少。奖励相当于坡度的权重,高奖励(正奖励)动作的坡度更值得攀爬。参数更新表示为 θ ← θ + α ⋅ ∇ θ log π θ ( a ∣ s ) ⋅ R θ←θ+α·∇_θ\log{π_θ (a|s)}·R θ←θ+α⋅∇θlogπθ(a∣s)⋅R, α α α为学习率。
在迷宫问题中,策略网络输出每个动作的选择概率,根据概率分布采样选择动作,若执行动作后获得高奖励,则对应动作的概率将被增加,若获得低奖励,则对应动作的概率将被降低。
计算梯度需要公式,有了自变量和因变量才能知道函数的梯度。我们可以这样理解:自变量是策略网络的参数,曲线/曲面是动作的概率,不同状态有不同曲线,我们的目标是找到一组参数,在不同的状态下生成的动作都表现的非常好,这里不一定动作就是极值,所以梯度不一定是朝着每个动作都是最大的方向。
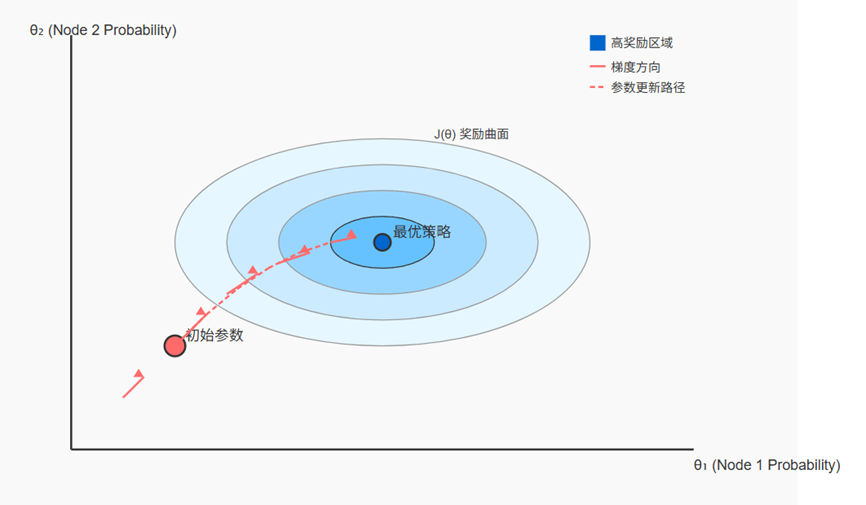
再一步抽象为变量是策略网络的参数,目标函数(因变量)是策略产生的轨迹的期望累积奖励。我们的目标是找到一组参数,在不同的状态下生成的奖励都是非常大的,这里要找的就是极值,但它是如何由参数映射成极值的是隐式的。
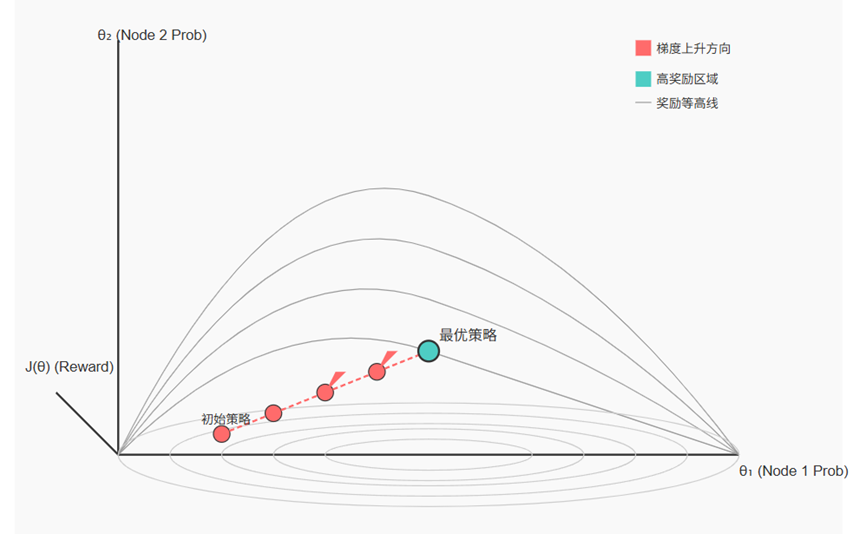
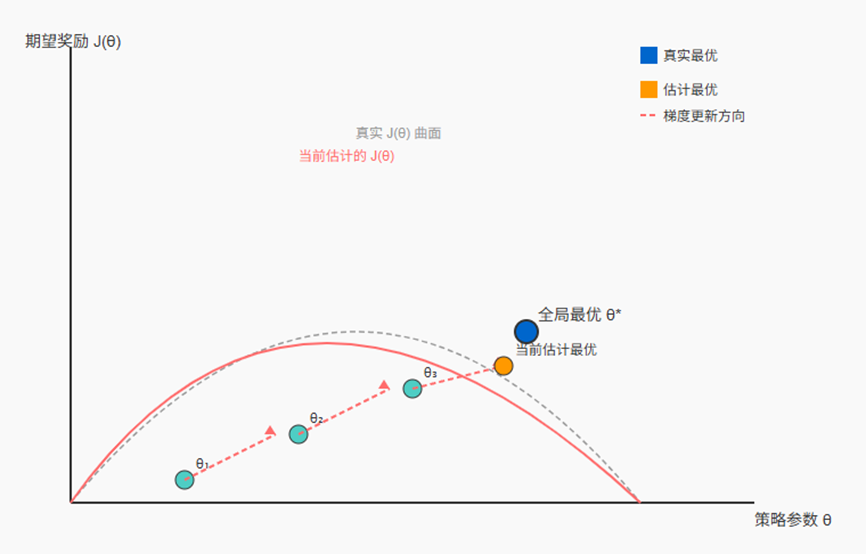
梯度的含义表示参数的微小变化对期望奖励的影响。我之前一直执着于将动作与奖励产生联系,是因为我以为曲线的表达式是固定的,但实际上因为不同动作计算的奖励不一样,所以奖励是可变的,也就是说函数的形状并不固定,参数的变化会改变动作概率的变化,从而改变奖励和期望奖励的形状。策略梯度定理是用对数概率梯度来近似奖励函数的梯度,策略梯度定理的蒙特卡洛估计的梯度仅基于单条轨迹,是对真实期望梯度的有偏估计,我们只需要沿着梯度的方向更新参数,找到使期望奖励最大的参数。正因如此,有一些稳定性策略,例如:
- 批量梯度估计(Batch Gradient Estimation),通过平均减少单条轨迹的随机性影响,使梯度更接近真实期望。
- 优势函数(Advantage Function),表示动作在状态下的优势,可以减少梯度方差,区分动作好坏。
- PPO算法中使用截断的重要性采样,限制策略更新幅度。
【更新中,欢迎交流】
参考来源:
@ AIGC
策略梯度定理公式的详细推导
#14 正交子空间
数学基础 – 线性代数之格拉姆-施密特正交化
正交向量和子空间























 1860
1860

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








