GCD的题目

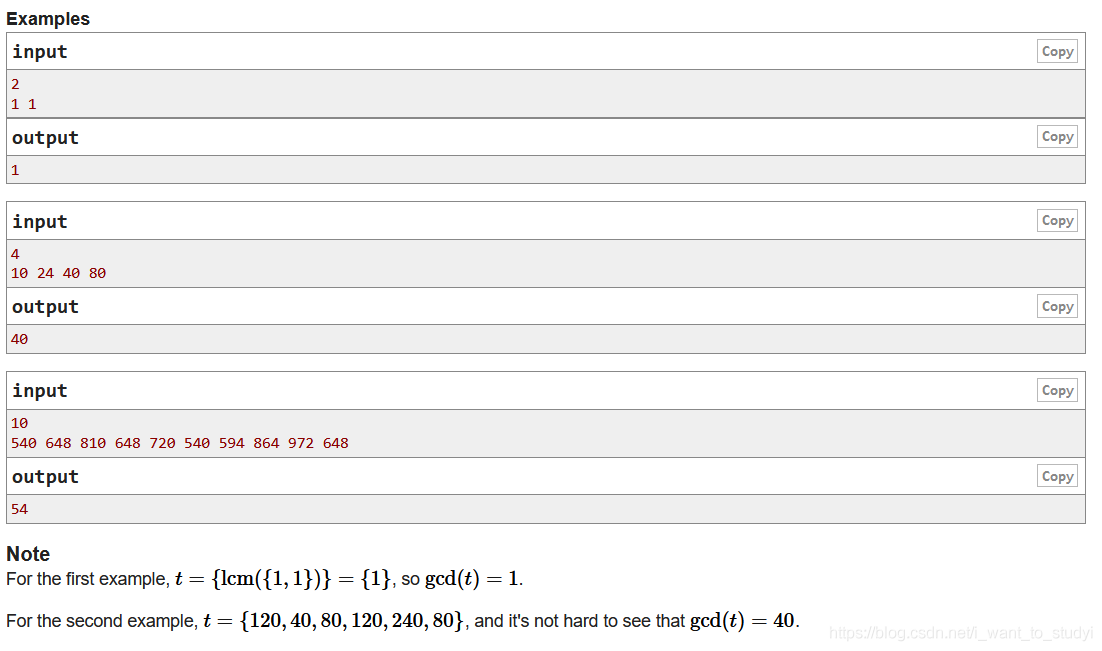
题意:

对于正整数的多集合a={a0,a1,...,ak}，定义s的最大公除数（GCD）和最小公倍数（LCM）如下。

gcd(a)是最大的正整数x，使得s中的所有整数都能在x上被除。
lcm(a)是最小的正整数x，它能被s中的所有整数整除。
例如，gcd({8,12})=4,gcd({12,18,6})=6和lcm({4,6})=12。注意，对于任何正整数x，gcd({x})=lcm({x})=x。

Orac有一个长度为n的序列，他想出了一个多集t={lcm({ai,aj}) | i<j}，并要求你为他找到gcd(t)的值。换句话说，你需要计算给定序列中所有元素对的LCM的GCD。

先说结论：(红字)
已知数组a = {a0,a1,...,an - 1}
已知gcd0 = gcd{ lcm(a0,a1) , lcm(a0,a2),lcm(a0,a3), ... ,lcm(a0,an-1) }

                 =gcd(a0,lcm(a1,a2，…，an-1))  
       gcd1 = gcd{ lcm(a1,a2) , lcm(a1,a2),lcm(a1,a3), ... ,lcm(a1,an-1) }

                 =gcd(a1,lcm(a2,a3，…，an-1))
       gcd2 = gcd{ lcm(a2,a3),lcm(a2,a4)，…，lcm(a2,an-1) }

                 =gcd(a2,lcm(a3,a4，…，an-1))
       ........

        gcdi = gcd{ lcm(ai,ai+ 1),lcm(ai,ai+2)，…，lcm(ai,an-1) }

                =gcd(ai,lcm(ai+1,ai+2…an-1))
      
推出res=gcd(gcd1,gcd2,…,gcdn)

代码：

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.math.BigInteger;
import java.nio.file.attribute.AclEntryFlag;
import java.security.AlgorithmConstraints;
import java.sql.Struct;
import java.text.CollationElementIterator;
import java.text.DateFormatSymbols;
import java.util.*;
import java.util.stream.Collectors;


public class Main
{
    static PrintWriter pw = new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
    static int N = (int)1e5;
    static math_myself math_me = new math_myself();
    static int a[] = new int[N]; // 原数组
    static int prefixgcd[] = new int[N]; // 前缀gcd数组
    static int suffixgcd[] = new int[N]; // 后缀gcd数组

    public static void main(String[] args ) throws IOException
    {
        int n = rd.nextInt();
        for(int i = 0 ; i < n ; i ++)  a[i] = rd.nextInt();

        // 计算前缀gcd数组
        prefixgcd[0] = a[0];
        for(int i = 1 ; i < n ; i ++)  prefixgcd[i] = math_me.gcd(prefixgcd[i - 1],a[i]);

        // 计算后缀gcd数组
        suffixgcd[n - 1] = a[n - 1];
        for(int i = n - 2 ; i >= 0 ; i --)  suffixgcd[i] = math_me.gcd(suffixgcd[i + 1],a[i]);

        int res = 0;
        for(int i = 0 ; i < n ; i ++)   res = math_me.gcd(res,math_me.lcm(suffixgcd[i + 1],a[i]));

        pw.println(res);
        pw.flush();
    }
}

class rd
{
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
    static StringTokenizer tokenizer = new StringTokenizer("");

    static String nextLine() throws IOException   { return reader.readLine(); }

    static String next() throws IOException
    {
        while (!tokenizer.hasMoreTokens())  tokenizer = new StringTokenizer(reader.readLine());
        return tokenizer.nextToken();
    }

    static int nextInt() throws IOException  { return Integer.parseInt(next()); }

    static double nextDouble() throws IOException { return Double.parseDouble(next()); }

    static long nextLong() throws IOException  { return Long.parseLong(next());}

    static BigInteger nextBigInteger() throws IOException
    {
        BigInteger d = new BigInteger(rd.nextLine());
        return d;
    }
}

class PII
{
    int x,y;
    public PII(int x ,int y)
    {
        this.x = x;
        this.y = y;
    }
}

class math_myself
{
    int gcd(int a,int b)
    {
        if(b == 0)  return a;
        else return gcd(b,a % b);
    }

    int lcm(int a,int b)
    {
        return a * b / gcd(a, b);
    }

    // 求n的所有约数
    List get_factor(int n)
    {
        List<Long> a = new ArrayList<>();
        for(long i = 1; i <= Math.sqrt(n) ; i ++)
        {
            if(n % i == 0)
            {
                a.add(i);
                if(i != n / i)  a.add(n / i);  // // 避免一下的情况：x = 16时，i = 4 ，x / i = 4的情况，这样会加入两种情况  ^-^复杂度能减少多少是多少
            }
        }

        // 相同因子去重，这个方法，完美
        a = a.stream().distinct().collect(Collectors.toList());

        // 对因子排序（升序）
        Collections.sort(a);

        return a;
    }
}