蓝桥杯：蛇形数组、曼哈顿距离

原创已于 2023-02-18 15:46:08 修改 · 180 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#蓝桥杯

于 2022-04-02 18:23:08 首次发布

蓝桥杯专栏收录该内容

44 篇文章

订阅专栏

这篇博客探讨了如何解决在蛇形矩阵中计算两个楼号间最短移动距离的问题。首先解释了蛇形矩阵的排列规则，并通过实例展示了矩阵的形态。接着，分析了如何确定楼号所在的行和列，特别是对于蛇形矩阵，偶数行和奇数行的列号处理方式不同。最后，给出了AC代码实现，通过计算行差和列差来得到最短距离。输入和输出格式以及数据范围都有明确说明，示例给出了具体解答。

距离：

对蛇形矩阵的理解：

正常的二维矩阵：

蛇形矩阵：（奇数行反转）

题目：

题目描述

X星球居民小区的楼房全是一样的，并且按矩阵样式排列。

其楼房的编号为 1,2,3…当排满一行时，从下一行相邻的楼往反方向排号。

比如：当小区排号宽度为 6时，开始情形如下：

1  2  3  4  5  6
12 11 10 9  8  7
13 14 15 .....

我们的问题是：已知了两个楼号 m和 n，需要求出它们之间的最短移动距离（不能斜线方向移动）。

输入格式

输入共一行，包含三个整数 w,m,n，w 为排号宽度，m,n为待计算的楼号。

输出格式

输出一个整数，表示 m,n两楼间最短移动距离。

数据范围

1 ≤ w, m,n ≤ 10000,

输入样例：

6 8 2

输出样例：

分析：

1、求行号

分析w = 6的时候：

每个数都减去1

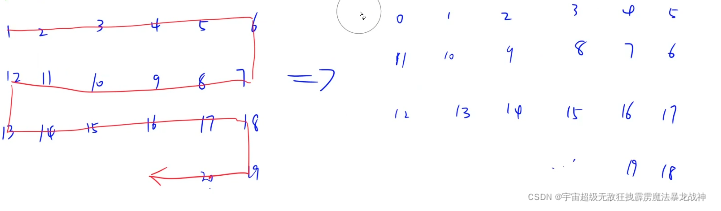
（因为这样比较容易算行标）

让行号列号从0开始，这样行号会特别好算：

假设要求数为n的话：

（行号和列号都与最近的上图相对应）

行号： x1 = m / w ；

x2 = n / w ；

2、求列号

假设正常二维数组的话求列号：

列号： y = m % w ,n % w;

若是蛇形数组的话：

正常二维数组列号为x的话，那么在蛇形数组下就是5 - x

由此可得出：

在蛇形数组中（奇数行）

y1 = w - 1 - m % w ；

y2 = w - 1 - n % w ；

AC代码：

#include<bits/stdc++.h>
#define endl '\n'
#define inf 0x3f3f3f3f

using namespace std;

typedef long long ll;

int main()
{   
    int w,m,n;
    scanf("%d %d %d",&w,&m,&n);
    m --,n --;
    
    int x1 = m / w, x2 = n / w;
    int y1 = m % w, y2 = n % w;
    if(x1 % 2 == 1)  y1 = w - 1 - y1;
    if(x2 % 2 == 1)  y2 = w - 1 - y2;
    
    printf("%d",abs(x1 - x2) + abs(y1 - y2));
    
    return 0; 
}