区间合并= =

原创已于 2022-02-22 13:28:17 修改 · 166 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2022-01-15 14:54:44 首次发布

算法专栏收录该内容

33 篇文章

订阅专栏

本文介绍了一种用于合并多个有交集区间的方法，并提供了一个具体的C++实现案例。通过该算法，可以有效地解决区间合并的问题，适用于如数据处理、任务调度等场景。

理解：

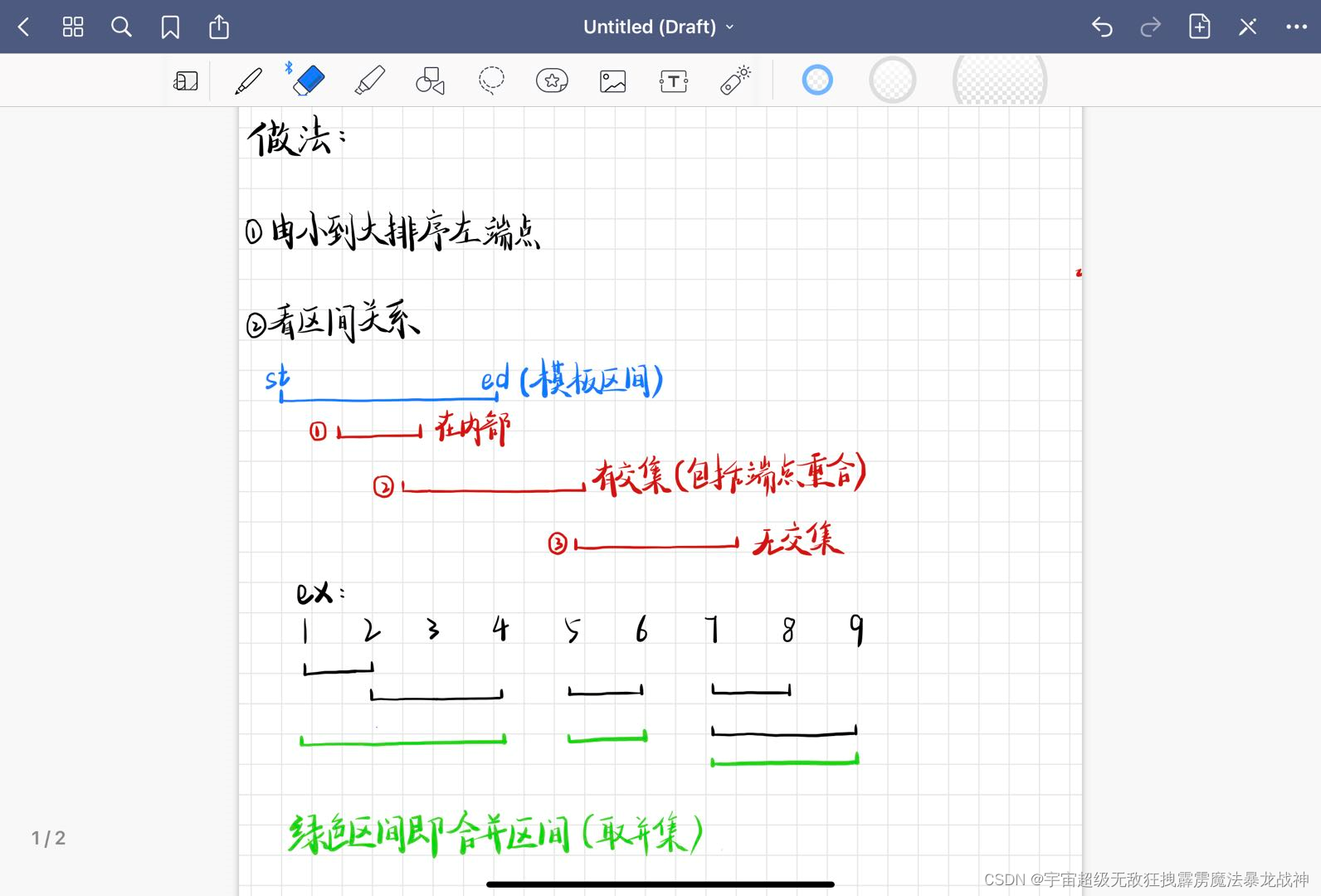
模板：

//将所有存在交集的区间合并
void merge(vector<PII> &segs)
{
	vector<PII> res;
	
	sort(segs.begin(),segs.end());
	
	int st = -2e9,ed = -2e9;
	for(auto seg : segs)
	{
		if(ed < seg.first)
		{
			if(st != -2e9) res.push_back({st,ed});
			st = seg.first,ed = seg.second;
		}
		else ed = max(ed, seg.second);
	}
	if(st != -2e9) res.push_back({st,ed});
	
	segs = res;
}

题目：

题目1：（区间合并裸题）

题目描述：

给定 n 个区间 [li,ri]，要求合并所有有交集的区间。

注意如果在端点处相交，也算有交集。

输出合并完成后的区间个数。

例如：[1,3]

和 [2,6] 可以合并为一个区间 [1,6]。

输入格式

第一行包含整数 n。

接下来 n行，每行包含两个整数 l 和 r。

输出格式

共一行，包含一个整数，表示合并区间完成后的区间个数。

数据范围

1≤n≤100000,−10^9≤li≤ri≤10^9

输入样例：

输出样例：

AC代码：

#include<bits/stdc++.h>

using namespace std;

typedef pair<int, int> PII;

//区间合并 
void merge(vector<PII> &segs)
{
	vector<PII> res;
	
	sort(segs.begin(),segs.end()); // C++中的pair排序会优先以区间的左端点进行排序，然后再排右端点 
	
	int st = -2e9,ed = -2e9; // st表示区间的左端点，ed表示区间的右端点 
	for(auto seg : segs) // 把segs中的元素全部遍历一遍
	{
		if(ed < seg.first) // 当前区间的右端点没接上下一个区间，属于第三种情况，两个区间是一点没接上啊
		{
			if(st != -2e9)  res.push_back({st,ed}); // ，如果不是最开始初试的区间，则把区间加到答案里面去 
			st = seg.first,ed = seg.second; 
		} 
		//否则就是当前区间和下一个区间是有交集的 
		else ed = max(ed, seg.second); // 取并集，更新为长度更长的长区间 
	} 
	
	if(st != -2e9)  res.push_back({st,ed}); //防止输出的数据没有任何区间 
	
	segs = res; // 把区间更新为res 
}

int main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(false);
	
    int n;
    cin >> n;
    
    vector<PII> segs; 
    for(int i = 0 ; i < n ; i ++)
    {
    	int l,r;
    	cin >> l >> r;
    	segs.push_back({l,r}); // 将每组l，r添加到数组segs中 
	}
	
	merge(segs);
	
	cout << segs.size() << endl; // 返回区间长度 
    
	return 0;
}