差分算法 = =

一维差分

1、理解：

2、板子：

给区间[l,r]中每个数加上c：B[l] += c,B[r + 1] -= c; 

3、构造b数组无敌的方法

我们可以先假想a数组为空，那么b数组一开始也为空，但是实际上a数组并不为空，题目中需要输入值，我们把a数组的每一个元素的值都是在b数组的基础上插进去的（因为b数组初始值为0），在插的过程，就构造好了b数组，完美无缺。

3、题目 ：

题目1：（差分裸题）

输入一个长度为 n的整数序列。

接下来输入 m个操作，每个操作包含三个整数 l,r,c，表示将序列中 [l,r] 之间的每个数加上 c。

请你输出进行完所有操作后的序列。

输入格式

第一行包含两个整数 n和 m。

第二行包含 n个整数，表示整数序列。

接下来 m行，每行包含三个整数 l，r，c，表示一个操作。

输出格式

共一行，包含 n个整数，表示最终序列。

数据范围

1≤n,m≤100000,
1≤l≤r≤n,
−1000≤c≤1000,
−1000≤整数序列中元素的值≤1000

输入样例：

6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1

输出样例：

3 4 5 3 4 2

AC代码：

#include<bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;

//最开始都是0，b数组初始的时候就是a的差分数组了 
int a[N]; // 原数组
int b[N]; // 差分数组 

void insert(int l, int r, int c)
{
	b[l] += c; // b[l]加上c，因为a[l] = b[1] + b[2] + ... + b[l],所以a[l]也会加上c，a数组中其它元素在[l,r]区间内的元素都会加上c 
	b[r + 1] -= c; // 加c减c抵消掉，使得b[r + 1]及其之后的元素保持原来状态  
}

int main()
{
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(false);
	
    int m,n;
    cin >> n >> m;
    
    for(int i = 1; i <= n ; i ++)  cin >> a[i]; // 每个元素都可以看成b数组每个元素插进去的 
    
    //for(int i = 1 ; i <= n ; i ++) ，b[i] = a[i] - a[i - 1]此语句与下面语句等价 
    for(int i = 1 ; i <= n ; i ++)   insert(i,i,a[i]);; // 要想[l,l]区间上a数组中加上a[i](本该输入的数字)，只需要b[l] + a[i] 
    
    while(m --)
    {
    	int l,r,c;
    	cin >> l >> r >> c;
    	insert(l,r,c); // 对b数组进行加c 
	}
	
	//对b数组求前缀和后，b[i]存储的就是前缀和数组 
	for(int i = 1 ; i <= n ; i ++)  b[i] += b[i - 1];
	
	for(int i = 1 ; i <= n ; i ++)  cout << b[i] << ' ';
	
	return 0;
}

题目2：江西ICPC省赛K题It rains again

思路：显然，y坐标是不需要分析的

代码里需要解释得就是sum[起点]++和sum[终点]++

想一下，拓扑排序的板子里是不是有类似的处理方式，就是多个点只想同一终点的时候，终点--，是的，我们这里的sum就是存储到达该点的点的数量，然后以1为单位枚举每个点，只要该点不是0，就代表这个点是某个长度里面的点，要把他的长度加进来

怎么做呢，大家想，如果有两个起点和终点一样的点，起点是2，终点是-2

两个点都是从1开始到3结束，那么就是sum[1]=2，sum[3]=-2；

那么我们从1开始枚举，枚举1，sum[1]！=0，所以ans++，然后将sum[2]+=sum[1]，枚举2，sum[2]=1，ans++，sum[3]+=sum[2]，这边就是-2+2，所以就是0，这边的实际意义是两个到该点的x到这就结束，往后就没有了。

然后所有的情况，比如说两个重合的边，交叉的边，还有一个边包另一个边的情况，都可以用这种方法做出来，没必要特判。

然后所有的情况，比如说两个重合的边，交叉的边，还有一个边包另一个边的情况，都可以用这种方法做出来，没必要特判。

AC代码：

#include <bits/stdc++.h>
using namespace std;
 
const int N = 100010;
int sum[N];
int ans;
int main()
{
	
	int t ;
	
	cin>>t;
	
	for(int i = 1 ; i <= t ; i++)
	{
		int x,y;
		int a, b;
		
		cin>>a>>b>>x>>y;
		
		sum[a]++;
				
		sum[x]--;
	}
	for(int i = 1 ; i < N ; i++)
	{
		sum[i]+=sum[i-1];
		if(sum[i]!=0)
			{
				ans++;	
			}
	}
	
	
	cout<<ans;
	
}

二维等分

1、理解：

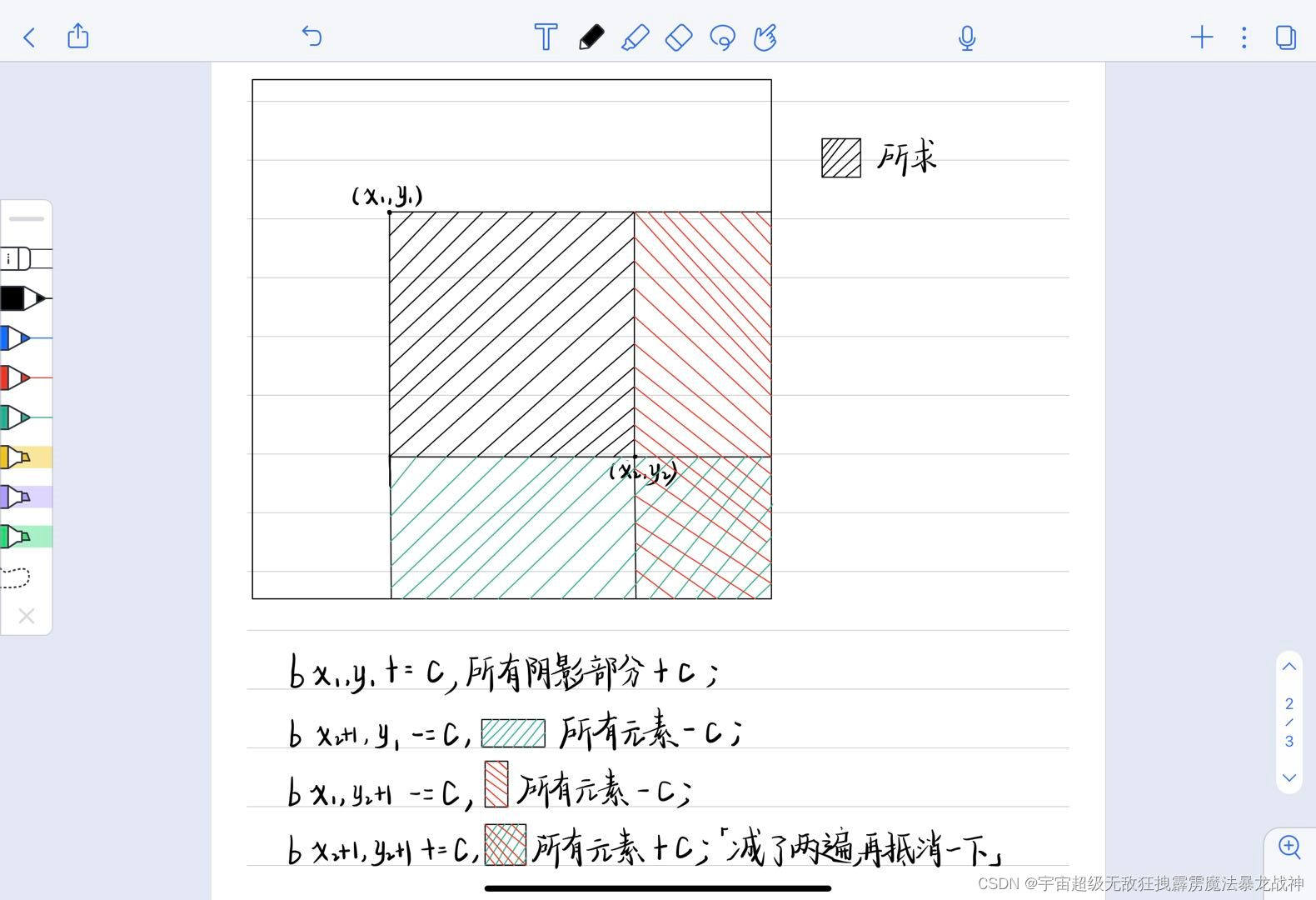
2、板子：

给以(x1,y1)为左上角，(x2,y2)为右下角的子矩阵中的所有元素加上c:
S[x1,y1] += c; S[x2 + 1,y1] -= c; S[x1,y2 + 1] -= c; S[x2 + 1,y2 + 1] += c;

题目：

最高的牛

有 N 头牛站成一行，被编队为 1、2、3…N，每头牛的身高都为整数。

当且仅当两头牛中间的牛身高都比它们矮时，两头牛方可看到对方。

现在，我们只知道其中最高的牛是第 P 头，它的身高是 H ，剩余牛的身高未知。

但是，我们还知道这群牛之中存在着 M 对关系，每对关系都指明了某两头牛 A 和 B 可以相互看见。

求每头牛的身高的最大可能值是多少。

注意：

• 此题中给出的关系对可能存在重复

思路

题目要保证每头牛尽可能的高，同时又要满足题目给的m对关系，让他们相互之间能够看得见，两头牛要相互看得见，那么两头牛之间的其他牛的高度就必须小于两头牛，不能相等。既要尽可能的高，又要小于，那么就是比两个牛小1就可以。那么我们该如何处理每一对给出的关系，自己手动手动模拟模拟样例就可以发现，每当给出一组(l,r),[l + 1,r - 1]，​​这个区间的数必须全部减1，才能满足，不改变前面已经给出的关系​。把一个区间内的数减1，可以用到差分来做，最后的答案，就是求一个前缀和就是原数组。

题目给的数据可能会重复，所以我们可以用一个哈希表来判断是否出现过。

AC代码：

#include<bits/stdc++.h>
 
using namespace std;
 
const int N = 1e5 + 10;
int a[N];
int d[N]; // 差分数组

int main()
{
    int i;
    int n,p,h,m;
    int l,r;
    set<pair<int,int>>exit;
    cin >> n >> p >> h >> m; 
    d[1] = h;
    while(m --)
    {
    	cin >> l >> r;
    	if(l > r)  swap(l,r);
    	if(!exit.count({l,r}))
    	{
    		exit.insert({l,r});
    		d[l + 1] --;
    		d[r] ++;
		}
	}
	for(i = 1 ; i <= n ; i ++)
	{
		d[i] += d[i - 1];
		cout << d[i] << endl;
	}
    return 0;
}