零.写在前面
上学期在《复变函数与积分变化》中接触到了傅里叶变换,当时仅仅是会进行一些运算,对于其背后的意义和实际的用处一无所知。这个学期在《自动控制原理》中使用拉式变换将时域上的问题转化到频域上,使用伯德图和奈奎斯特图进行频率分析;在《数字图像处理》的频率域图像滤波中使用离散傅里叶变换进行低通滤波、高通滤波等;在《算法设计与分析》的分治算法中提到了FFT,这也是本文的起因。
目录
一.背景介绍:从傅里叶变换到离散傅里叶变换
一般的傅里叶变换对于采集、存储离散值的计算机而言并不好处理,一般要将其做一些离散化的变换。
首先,在时间(t域)上离散地采样,对应的傅里叶变换(FT)也变为离散时间傅里叶变换(DTFT)

然后,对于得到的DTFT在频率(w域)上离散地采样,得到DFT。其形式如下:

其中W项为 以此将在x域上的
在一个周期(
)内离散化到n域上(n=0~N-1)。
至此将傅里叶变换(FT)最终转化为离散傅里叶变换(DFT)
二.从分治角度看FFT:
函数的点值法表示:
在背景介绍中曾提到计算机中习惯以离散值存储。对于多项式函数一般采用点值表示法来替代系数表示法,对于一个n-1次多项式可以通过n个不同点唯一表示。
其优势不仅体现在存储上,在计算方面点值表示法也有其优势。对于函数间相乘系数表示法需要O(n^2)而点值表示仅需要O(n)。
听起来非常好,那么对于系数表示多项式我们的目标就是将其化为点值表示。由此引出了问题——如何转化?
对于一个n-1阶多项式若直接计算其一个值时间复杂度为O(n^2),若将其(An*x^n-1+An-1*x^n-2...A2*x+A1)表示为A1+(x*(A2+x*(A3+x*...(An-1+x*An)...)))可优化时间复杂度为O(n),然而这样是不够的——若将系数表示的函数先转化为点值表示(计算n个点,每个点用时O(n))再计算相乘,时间复杂度为O(n*n+n)=O(n^2),相比系数表示并没有优势。那么我们此时要解决的问题就是如何加速点值的运算?
如何加速点值计算:
为了方便讲解,以F(x)=x^7+x^6+x^5+x^4+x^3+x^2+x+1为例
第一步:
考虑到点值表示源于取点计算函数值,如果对所取点进行特殊化可能能起到减少计算的效果,由此我们基于函数的对称性进行第一次特殊化。
任何一个多项式都可以分成x^2k和x^2k+1(k=0....N)两部分,前者为偶函数f(-x)=f(x)后者为奇函数g(-x)=-g(x),由此对F(x)=f(x)+g(x)有F(-x)=f(x)-g(x)。
原:F(x)=x^7+x^6+x^5+x^4+x^3+x^2+x+1;x={-1,1,-2,2,-3,3,-4,4}
变化后:f(x)=x^6+x^4+x^2+1;g(x)=x^7+x^5+x^3+x;x={1,2,3,4}
基于此将多项式拆分后,对于点的计算量减为原来的1/2,但这样是不够的,时间复杂度并没有改变。
第二步:
若所得的f(x)和g(x)总能进一步拆分,则可将问题写成T(n)=2*T(n/2)+Cn,根据主定理其时间复杂度为O(n*logn)。新的问题产生:如何将函数拆分?
只需要令t=x^2,f(x)=f1(t), g(x)=x*g1(t),这样f1(t),g1(t)就与F(x)形式类似,可以相类似的进行拆分。
原:f(x)=x^6+x^4+x^2+1;g(x)=x^7+x^5+x^3+x;x={1,2,3,4}
变化后:f1(t)=t^3+t^2+t+1;g1(t)=t^3+t^2+t+1;t={1,4,9,16}
由这个拆分又产生了新的问题:除最后一次以外,每一次拆分得到的新变量总是要正负成对出现,从而使下一次拆分后得到的函数代入一个值能解出当前函数的两个值(一正一负)。如同F(x)和F(-x)要同时出现,f1(t)和f1(-t)也要同时出现。 这个问题在实数域上是无法解决的,在实数域上和
(
)是无法同时有意义的。于是我们将x的取值扩充到复数域。
第三步:
对于我们要取的N个点,取X(k)=e^(-i*2π*k/N)(其中k=0,1...N-1)。此时每次拆分分为两步:1.拆分使用奇偶性后取右半平面的值。2.令t=x^2,将arg(x)变为两倍,并令之为t。其过程大致如下:
原来x的取值: 取右半平面后:
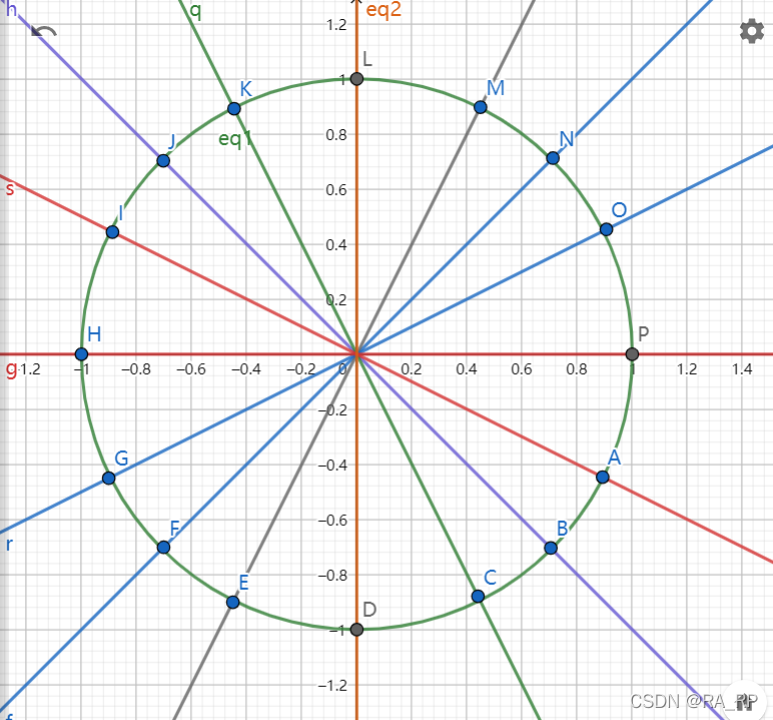
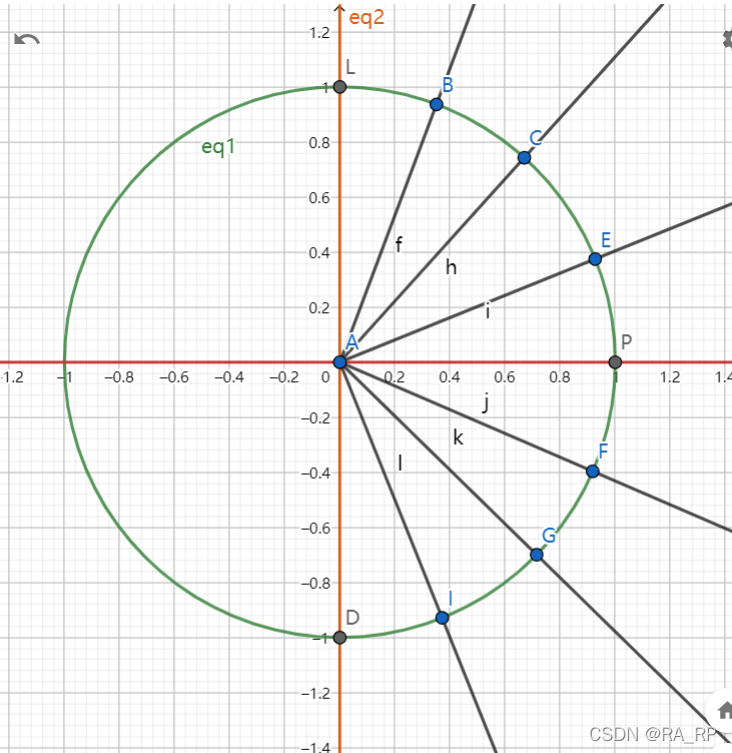
最终t=x^2的取值:
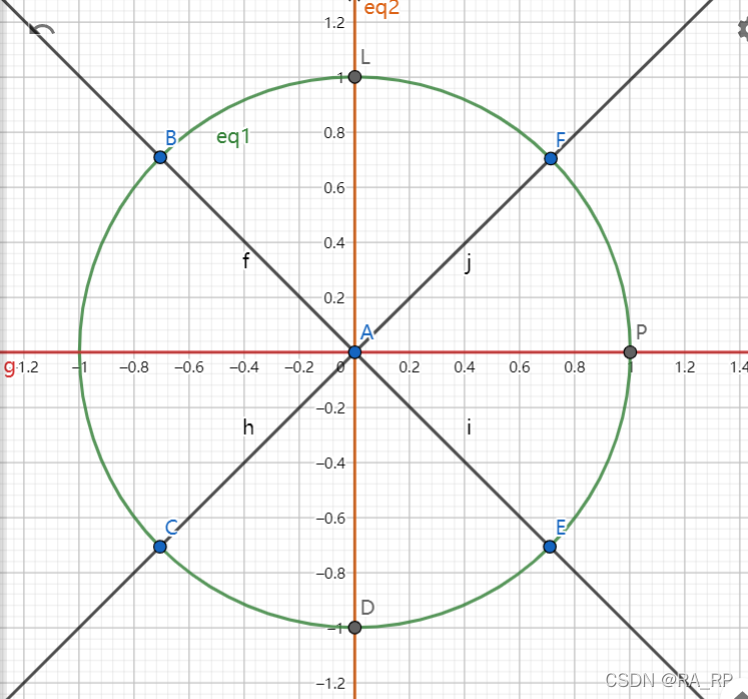
从而实现了每次拆分后总有成对的相反数。
综上步骤可以实现基于分治的FFT。
三.从傅里叶变换的角度看FFT:
为什么这种分治算法叫作FFT?计算一个N阶多项式的点值表示又与傅里叶变换有什么关系?
我们先关注离散傅里叶变换的形式:在一个周期内的一维离散傅里叶变换
将之与分治方法实现的第三步中的X(k)=e^(-i*2π*k/N)相比我们可以发现X[k]等价于。令:
;同时f(x)与x一一对应,可视为多项式的系数与次数。由此可以写成:
,与在分治方法中提到的多项式结构一致。与一开始的多项式的略微区别在于其将W域映射到了w域。
由上述转换我们不难发现,从本质上看:计算一个N阶多项式的点值表示等价于对其进行傅里叶变换。傅里叶变换的意义是将一个函数使用正弦函数进行插值,得到的频域函数实质上也是经过变化的点值表示。傅里叶变换可以看成多项式点值表示的一般化,可以将除多项式外的函数也进行“点值表示”。
四.FFT对于CNN的加速:
在学《数字图像》的时候不难发现:各种滤波器都不过在人类的直观视角下比较适合特征提取的卷积,然而可能真实情况更为复杂,人类难以找出其中特质。由此CNN中通过反向传播算法去寻找可能超出人类认识的特征,可谓是取代了各种传统的图像域滤波。既然CNN中用到了图像域滤波,那么难免就会产生疑问,频率域滤波去哪里了?
在《复变函数》中曾提到,原域上的卷积等价于频率域上的点积。由此不难想到:是否可以通过进行FFT然后再计算点积的方式,加速CNN中卷积层的运算呢?
以我刚用过的YOLO网络为例:
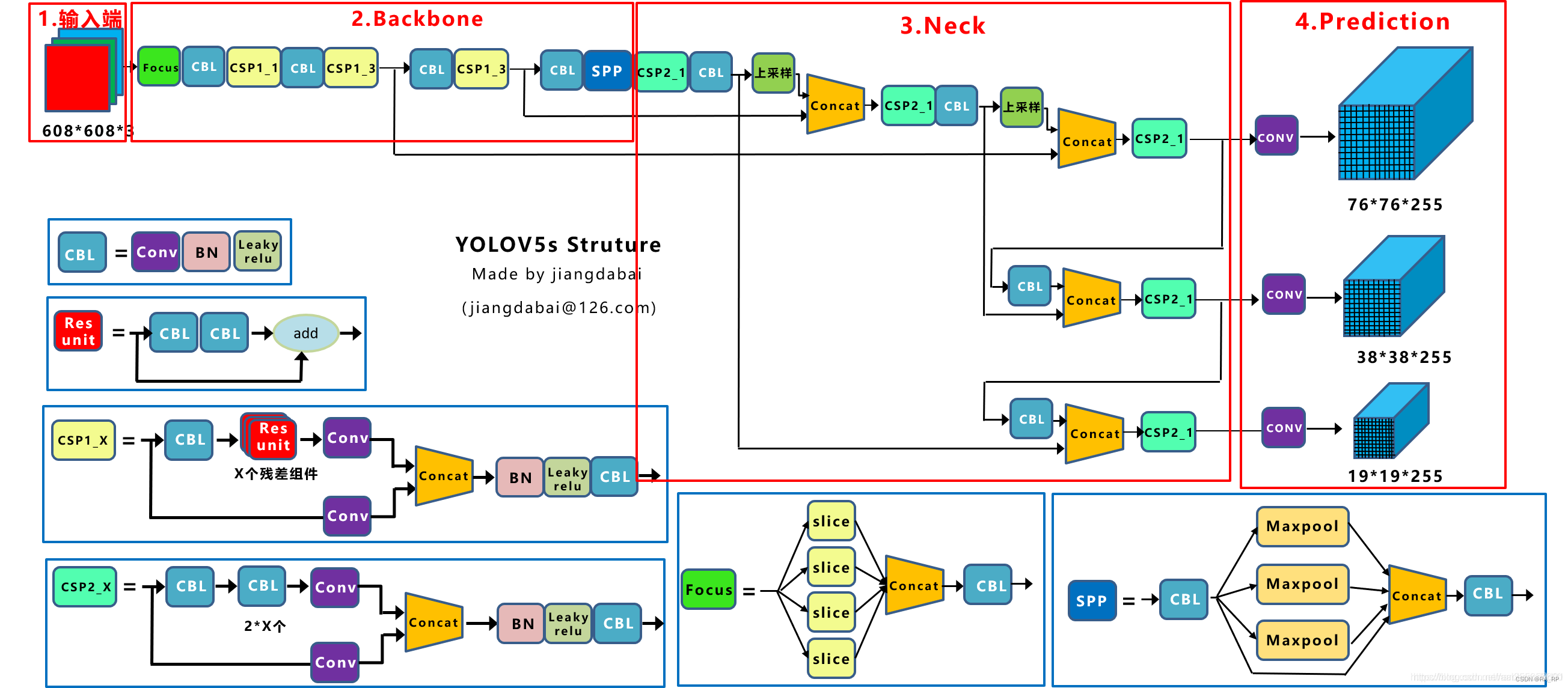
对于其中的第一个卷积层,其输入尺寸为152*152,卷积核为3*3,如果直接使用卷积运算
计算量为:
若使用FFT,其计算量为:
2+64*2是考虑了x,y两个方向的变换,再加上逆变换。
可以看到FFT确实减少了计算量。而且,在具体操作中可以不用每步都变换回去,故有些时候不需要IFFT也不用FFT变换,由此计算量:8976953,接近于使用FFT加速后整个网络的卷积计算量,其速度大体上会是不进行变化的几十倍。
然而,FFT加速也有其缺点——计算机进行复数运算开销大,由此其实际的效果会大打折扣。
五.WinoGrad加速CNN:
现在主流的CNN加速,采用的基本上是WinoGrad。在我不理解YOLO为什么不用FFT加速运算的时候,其实pytorch本身就自带了WinoGrad加速。FFT是通过复数变换到频率(w)域,其是通过优化计算时候的冗余,通过实数域的加减乘除,将问题转至m域。
具体解析可以看这篇写的很好的文章:详解卷积中的Winograd加速算法 - 知乎




















 4833
4833

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








