清华提出MoPPS，将贝叶斯流式推断引入提示选择领域，加速Reasoning Model训练

原文：https://mp.weixin.qq.com/s/55qRa7pVuWKOI-v9BxK4nw

论文题目： Can Prompt Difficulty be Online Predicted for Accelerating RL Finetuning of Reasoning Models?
论文链接： https://arxiv.org/abs/2507.04632
文章作者： Yun Qu, Cheems Wang, Yixiu Mao, Vincent Tao Hu, Xiangyang Ji
研究机构：清华大学季向阳教授THU-IDM团队，德国慕尼黑大学CompVis/原Stable Diffusion团队

前言

在大型语言模型（LLM）的强化学习微调中，计算效率与推理能力提升如同天秤的两端：传统方法要么随机采样提示，效率低下；要么依赖昂贵的实时评估，计算成本高昂。这一困境的核心矛盾在于：提示难度的动态评估需要LLM推理，而推理过程本身正是计算瓶颈所在。

清华大学季向阳团队与德国Stable Diffusion团队(CompVis)的最新研究提出了Model Predictive Prompt Selection(MoPPS)，为突破推理大模型训练效能瓶颈提供了新思路。该框架首次将贝叶斯流式推断引入提示选择领域，其核心创新可概括为三重设计：

1. 免评估的难度预测：提出首个基于生成式建模和贝叶斯流式推断的提示选择框架，将提示成功率建模为动态潜变量，通过Beta-Bernoulli共轭实现实时追踪（Spearman>0.5），节省79%LLM访问开销（图2）。

2. 计算-性能双赢机制：Thompson采样实现自动探索，在MATH/Countdown任务中达成1.8×加速与26%性能提升，首次替代Oracle评估（图5/表1）。

3. 即插即用通用性：兼容主流RL算法(PPO/GRPO等)和模型规模(1.5B~7B)，建立主动微调新范式。实验证明，MoPPS在数学证明、程序规划、几何推理三大挑战中均展现出较高计算效率。

MoPPS通过预测-优化闭环重构LLM微调路径，实现基础模型高效训练。

摘要

近年来的研究表明，强化学习（RL）微调在提升大型语言模型（LLMs）推理能力方面非常有效。然而，这一优化过程通常需要大量迭代才能达到令人满意的性能，因而带来了高昂的计算成本，其主要原因在于频繁的提示（prompt）评估、大量的LLM交互以及多次策略更新。合适的在线提示选择方法通过在训练过程中优先选择信息量大的提示来减少迭代次数，然而整个流程仍然严重依赖对提示的穷尽性评估和子集选择进行优化，这导致由于频繁的LLM推理调用而带来了巨大的计算开销。

本工作区别于传统的“评估后选择”方法，研究了一种面向任意提示的迭代式近似评估机制，并提出了MoPPS（Model Predictive Prompt Selection），这是一种基于贝叶斯风险预测的框架，用于在不依赖昂贵LLM交互的前提下估计提示难度。

在技术上，MoPPS将每个提示的成功率建模为一个潜变量，执行流式贝叶斯推断，并在构建的多臂老虎机模型中使用后验采样，从而实现高效、可适应的提示选择策略。

在数学、规划、以及基于视觉的几何任务上的大量实验证明，MoPPS能够稳定地预测提示难度，并显著减少LLM推理次数，从而加快训练速度。

图1：在训练过程中，我们的贝叶斯代理模型所预测的提示难度与经验成功率之间的 Spearman 等级相关系数及其 $p$ 值。

强相关性表明，我们的方法能够在不依赖高成本 LLM 推理的情况下，有效预测提示的难度。

1. 引言

强化学习（RL）微调是提升大型语言模型（LLMs）能力的重要方法（Guo等，2025），在数学问题求解（Luo等，2025b）和代码生成（Luo等，2025a）等任务中表现出显著效果。然而，RL微调的计算与内存成本较高，因其需密集rollouts进行策略评估（Zheng等，2025）。

在线提示选择在RL微调中至关重要： RL微调中，随机采样提示效率低下，难以捕捉信息性提示（Zheng等，2025）。近期研究探索了动态选择方法（Cui等，2025；Bae等，2025），如DAPO算法，通过过滤低质量或强调中等难度提示来优化训练。但这些方法因频繁调用LLM评估提示，仍面临高昂开销（Chen等，2025）。

摊销提示评估的希望与挑战: 模型预测任务采样（MPTS）（Wang等，2025a）通过轻量级预测模型估计效用，有望降低评估成本。然而，将其应用于LLM微调存在挑战：(i) 提示数据为离散token，缺乏连续标识符；(ii) 成功率分布动态变化，难以建模。

图2：不同提示选择方法在 Countdown 任务上的性能与计算效率对比。我们提出的 MoPPS 在训练效率与性能方面均优于均匀选择策略，同时相比于 DS 方法（Yu 等，2025），将 rollouts 的计算开销减少了 79%。

意识到在线评估提示难度对于高效地对LLMs进行强化学习微调的重要性，并结合上述挑战，本文旨在回答以下两个研究问题（RQs）：

1. 能否无需LLM额外交互动态预测提示难度？
2. 如何利用预测结果增强LLM推理能力？

面向主动选择的提示难度近似推断: 针对上述两个研究问题，本文提出了模型预测提示选择（MoPPS）策略，用于以摊销方式在线评估提示难度。该方法实现简单，却能显著提升RL微调中的学习效率。在此，我们将在线提示选择建模为一个序贯决策问题，并通过动态伯努利老虎机模型（Berry, 1972；Russo & Van Roy, 2014）进行求解。换言之，每个提示被视为一个拉杆，其随机二值奖励来源于以成功率为潜变量的分布；然后我们采用后验采样的方式，对提示进行流式筛选。对潜变量的采样结果避免了对所有提示的完全评估，作为一种随机乐观性（stochastic optimism）促进了探索，并支持在无需额外LLM推理调用的情况下进行信息性提示的选择。

贡献与主要发现: 本研究采用“预测后优化”（predict-then-optimize）的原则，成功将MPTS的理念应用于LLMs的强化学习微调实践中。主要贡献包括以下三点：

1. 提出概率图模型，将成功率作为潜变量，为LLM样本主动选择提供新范式。
2. 设计高效后验更新方法，替代昂贵评估。
3. 框架简洁，兼容多种RL算法与LLM主流Backbone。

在数学、规划和基于视觉的几何等复杂推理任务上的大量实验，表明 MoPPS 能够可靠地预测提示难度，与真实提示评估结果表现出高度相关性。得益于这种可预测性，我们的方法显著加快了 RL 微调过程，例如在 Countdown 任务上相比均匀采样实现了 $1.8\times$ 的训练加速（Pan 等，2025），并取得了更优的最终性能，例如在训练于 MATH 数据集（Hendrycks 等，2021）时，在 AIME24 数据集上实现了超过 $26\%$ 的相对性能提升。

更重要的是，我们的方法仅使用 $21\%$ 的 rollouts，就达到了与依赖大量评估的动态采样方法（Yu 等，2025）相当的性能，从而显著降低了计算成本。

2 初步内容

2.1 符号说明

在推理任务中，提示$\tau$可以表现为数学或逻辑推理问题，例如MATH 数据集中的问题
“多项式$(4+5x^3+100+2\pi x^4+\sqrt{10}{x}^4+9)$ 的次数是多少？”
设 T = { τ i } i = 1 N \mathcal{T}=\{\tau_i\}_{i=1}^N T={τi​}i=1N​表示完整的提示池，其中每个 ${\tau }_i$ 代表一个唯一的提示。我们将第 $t$ 次训练步骤中 LLM 的参数表示为 ${\pi }_{{\theta }_t}$。第 $t$ 步中被选中的提示批次记作 T t B = { τ t , i } i = 1 B ⊂ T \mathcal{T}_t^{\mathcal{B}}=\{\tau_{t,i}\}_{i=1}^{\mathcal{B}}\subset\mathcal{T} TtB​={τt,i​}i=1B​⊂T，其中 $\mathcal{B}$ 表示批量大小。

在第 $t$ 次时间步的 LLM 给定的情况下，提示评估指的是生成响应的阶段，即 LLM 在给定提示 $\tau$ 的条件下生成 $k$ 个独立的响应 y τ t = { y τ t , j } j = 1 k y^t_\tau = \{y_\tau^{t,j}\}_{j=1}^k yτt​={yτt,j​}j=1k​，其中每个 $y_{\tau }^{t,i}$ 是通过自回归方式采样得到的。在这里，我们将每个提示 $\tau$ 关联一个成功率 ${\gamma }_{\tau }^t\in [0,1]$，并将其视为潜在变量，表示在当前策略下该提示成功解决问题的概率。对于提示批次的成功率集合记为 Γ t B = { γ τ t , i t } i = 1 B \Gamma_t^{\mathcal{B}} = \{\gamma^t_{\tau_{t,i}}\}_{i=1}^{\mathcal{B}} ΓtB​={γτt,i​t​}i=1B​。然后，通过检查每个响应的真实答案，对其进行评分，从而得到一个二值奖励函数：

$$r_{\tau }^{t,j}\sim \mathrm{Bernoulli}({\gamma }_{\tau }^t),r_{\tau }^{t,j}=\{\begin{array}{ll}1,& \text{if response j is correct},\\ 0,& \text{otherwise},\end{array}j=1,\dots ,k.$$

对于每个提示 $\tau$，记 r τ t = { r τ t , i } i = 1 k r^t_{\tau} = \{r_{\tau}^{t,i}\}_{i=1}^k rτt​={rτt,i​}i=1k​ 为该提示生成的 $k$ 个响应所对应的奖励集合。第 $t$ 步中提示批次的馈结果记为 R t B = { r τ t , i t } i = 1 B \mathcal{R}_t^{\mathcal{B}} = \{r^t_{\tau_{t,i}}\}_{i=1}^{\mathcal{B}} RtB​={rτt,i​t​}i=1B​。因此，在给定 $r_{\tau }^t$ 的条件下，观察到 ${\gamma }_{\tau }^t$（即成功次数）的似然函数服从二项分布：

$$p(r_{\tau }^{t,i})=({\gamma }_{\tau }^t{)}^{[r_{\tau }^{t,i}=1]}\cdot (1-{\gamma }_{\tau }^t{)}^{[r_{\tau }^{t,i}=0]}\Rightarrow p(r_{\tau }^t\mid {\gamma }_{\tau }^t)=({\gamma }_{\tau }^t{)}^{s_{\tau }^t}\cdot (1-{\gamma }_{\tau }^t{)}^{k-s_{\tau }^t}\text{with}{s}_{\tau }^t\triangleq \sum _{j=1}^k{r}_{\tau }^{t,j}.(1)$$

为简化起见，本文在强化学习微调中聚焦于二值奖励信号。然而，所提出的方法也可直接扩展至更丰富的奖励形式，例如格式化奖励（Pan 等，2025），可以通过直接建模，或通过设定阈值或四舍五入的方式将其二值化来实现。

最后，我们将截至第 $t$ 步的完整优化历史记为 H t = { T i B , R i B } i = 0 t H_t = \{\mathcal{T}_i^{\mathcal{B}}, \mathcal{R}_i^{\mathcal{B}}\}_{i=0}^t Ht​={TiB​,RiB​}i=0t​，即所有被选中的提示批次及其在各轮迭代中的对应反馈。

2.2 对 LLM 的强化学习微调

强化学习微调的目标是优化 LLM 的参数 $\theta$，以最大化在提示分布上的期望奖励。在数学上，这对应于：

$$\underset{\theta }{\max }{\mathbb{E}}_{\tau \sim \mathcal{T},y\sim {\pi }_{\theta }(\cdot |\tau )}\left[r(\tau ,y)\right],(2)$$

其中，${\pi }_{\theta }(y|\tau )$ 表示模型在给定提示 $\tau$下对响应 $y$ 的条件分布，$r(\tau ,y)$ 是一个奖励函数，用于评估在提示 $\tau$ 下响应 $y$ 的质量。

群体相对策略优化（GRPO）。GRPO（Shao 等，2024）以组归一化的方式估计优势函数，消除了对价值函数的依赖。对于每个提示 $\tau \in {\mathcal{T}}_t^{\mathcal{B}}$，模型从旧策略 ${\pi }_{{\theta }_{\text{old}}}$ 生成 $k$ 个 rollout { y τ i } i = 1 k \{y_\tau^i\}_{i=1}^k {yτi​}i=1k​。GRPO 的优化目标被表示为：

J GRPO ( θ ) = E τ ∼ T t B ,    { y τ i } i = 1 k ∼ π θ old ( ⋅ ∣ τ ) [ 1 k ∑ i = 1 k 1 ∣ y τ i ∣ ∑ t = 1 ∣ y τ i ∣ ( min ⁡ ( ρ i , t ( θ ) ⋅ A ^ i ,    clip ( ρ i , t ( θ ) , 1 − ϵ , 1 + ϵ ) ⋅ A ^ i ) − β D K L ( π θ ∣ ∣ π ref ) ] , ( 4 ) \mathcal{J}_{\text{GRPO}}(\theta)=\mathbb{E}_{\tau \sim\mathcal{T}_t^{\mathcal{B}}, \; \{y_\tau^i\}_{i=1}^k \sim\pi_{\theta_{\text{old}}}(\cdot|\tau)}\left[ \frac{1}{k}\sum_{i=1}^k\frac{1}{|y_\tau^i|}\sum_{t=1}^{|y_\tau^i|}\left(\min\left( \rho_{i,t}(\theta) \cdot\hat{A}_{i}, \;\text{clip}(\rho_{i,t}(\theta), 1 - \epsilon, 1 + \epsilon) \cdot\hat{A}_{i} \right) - \beta D_{KL}(\pi_{\theta}||\pi_{\text{ref}}\right) \right],\quad(4) JGRPO​(θ)=Eτ∼TtB​,{yτi​}i=1k​∼πθold​​(⋅∣τ)​ ​k1​i=1∑k​∣yτi​∣1​t=1∑∣yτi​∣​(min(ρi,t​(θ)⋅A^i​,clip(ρi,t​(θ),1−ϵ,1+ϵ)⋅A^i​)−βDKL​(πθ​∣∣πref​) ​,(4)

其中，${\rho }_{i,t}(\theta )=\frac{{\pi }_{\theta }(y_t^i|\tau ,y_{0:t-1}^i)}{{\pi }_{{\theta }_{\text{old}}}(y_t^i|\tau ,y_{0:t-1}^i)}$，${\pi }_{\text{ref}}$ 是一个固定的参考策略。KL 散度项用于惩罚策略与 ${\pi }_{\text{ref}}$ 之间的偏离程度，$\beta$ 控制正则化强度。第 $i$ 个响应的群体相对优势通过对 { r τ i } i = 1 k \{r_\tau^i\}_{i=1}^k {rτi​}i=1k​ 进行归一化计算得到：

A ^ i = r τ i − mean ( { r τ i } i = 1 k ) std ( { r τ i } i = 1 k . ( 5 ) \hat{A}_{i} = \frac{r_\tau^i-\text{mean}(\{r_\tau^i\}_{i=1}^k)}{\text{std}(\{r_\tau^i\}_{i=1}^k}.\quad(5) A^i​=std({rτi​}i=1k​rτi​−mean({rτi​}i=1k​)​.(5)

在线提示选择。
LLM强化学习微调的高计算成本推动了多项研究（Yu等，2025；Bae等，2025）探索在线提示选择方法。最新SOTA方法DS（Yu等，2025）发现GRPO算法在提示成功率为0/1时会出现梯度消失，因此采用过采样候选集${\mathcal{T}}_t^{\hat{\mathcal{B}}}\subseteq \mathcal{T}$（$\hat{\mathcal{B}}>\mathcal{B}$），通过过滤无信息提示构建训练批次。

T t B = { τ ∈ T t B ^    |    0 < ∑ i = 1 k r τ i < k    or    std ( { r τ i } i = 1 k ) > 0 } . ( 6 ) \mathcal{T}_t^{\mathcal{B}} = \left\{ \tau \in \mathcal{T}_t^{\hat{\mathcal{B}}} \;\middle|\; 0 < \sum_{i=1}^k r^i_\tau < k \;\text{or}\; \text{std}\left(\{r^i_\tau\}_{i=1}^k\right) > 0 \right\}. \quad(6) TtB​={τ∈TtB^​ ​0<i=1∑k​rτi​<korstd({rτi​}i=1k​)>0}.(6)

类似的思想也在 Bae 等（2025）和 Chen 等（2025）中被提出，这些方法优先选择成功率接近 0.5 的提示，并表明这种配置能提升优化效果。这些在线提示选择方法通过增加每个批次中有效提示的比例，从而减少迭代次数，达到加快训练的目的。然而，训练步数的减少是以增加精确 LLM 评估所带来的额外计算开销为代价的（Zheng 等，2025）。

2.3 模型预测任务采样（MPTS）

MPTS（Wang等，2025a）通过主动推理摊销策略评估成本，利用流式变分推断构建风险预测模型$p(\ell |\tau ,H_t;{\theta }_t)$，预测任务$\tau$的评估指标$\ell$（如策略回报）。结合采集准则（如置信上界或后验采样），实现高效主动采样，避免额外计算开销（Qu等，2025）。

在鲁棒自适应领域（Wang等，2023），MPTS展现了高效性（Qu等，2025）。但原始MPTS针对连续任务空间设计，而LLM微调涉及离散提示，缺乏显式任务标识符，且需减少迭代成本。本文改进MPTS，聚焦：（i）在RL微调中摊销提示评估成本；（ii）优化采样准则以加速训练。

3 方法

本节围绕第 1 节中的两个研究问题提出技术解决方案，并介绍一个用于加速强化学习微调的原理化且高效的框架——模型预测提示选择（Model Predictive Prompt Selection）。

首先，我们将强化学习微调重构为一个生成过程，并给出相应的概率图模型，其中成功率被视为潜在变量。为了摊销在线提示评估的成本，我们构建了一组伯努利老虎机模型，并通过贝叶斯推断来估计每个提示对应的成功率。

随后，我们采用汤普森采样（Thompson Sampling）来获得预测结果，并将其与具体的数据选择准则相结合，用于高效的强化学习微调。

3.1 将强化学习微调视为生成过程

强化学习微调过程涉及多个变量，例如 LLM 的参数 ${\theta }_t$、提示批次 ${\mathcal{T}}_t^{\mathcal{B}}$、生成的响应以及在迭代过程中得到的批次奖励信号 ${\mathcal{R}}_t^{\mathcal{B}}$。近期的研究进展（Yu 等，2025）表明，基于特定准则进行提示选择对于加速训练过程具有重要意义。

主动式强化学习微调的生成过程。 将上述要素结合起来，我们可以表示相关变量的联合分布，并将其因式分解如下：

$$p({\theta }_{0:T},{\mathcal{T}}_{0:T-1}^{\mathcal{B}},{\mathcal{R}}_{0:T-1}^{\mathcal{B}})=p({\theta }_0)\prod _{t=0}^{T-1}\underset{\text{Prompt Selection}}{\underbrace{p({\mathcal{T}}_t^{\mathcal{B}}\mid {\theta }_t)}}\underset{\text{Policy Optimization}}{\underbrace{p({\theta }_{t+1}\mid {\theta }_t,{\mathcal{R}}_t^{\mathcal{B}},{\mathcal{T}}_t^{\mathcal{B}})}}\underset{\text{Prompt Evaluation}}{\underbrace{\int p({\Gamma }_t^{\mathcal{B}}\mid {\mathcal{T}}_t^{\mathcal{B}},{\theta }_t)p({\mathcal{R}}_t^{\mathcal{B}}\mid {\Gamma }_t^{\mathcal{B}})d{\Gamma }_t^{\mathcal{B}}}},(7)$$

其中，提示选择项包含某种选择机制，而提示评估则关联于如图 3 所示的潜在变量集合，即成功率。

公式 (7) 中的提示评估项表明，生成响应需要多次进行 LLM 推理调用，这在计算上开销巨大但对于策略优化很必要，而且也被用于评估提示难度来进行在线筛选。当优化过程中未引入任何提示选择准则时，随机提示选择（例如 $\text{Uniform}({\mathcal{T}}_t^{\mathcal{B}})$）是与更新后的策略 ${\theta }_t$ 无关的，因此不会带来额外的推理开销。然而，正如 Yu 等（2025）所证明的那样，随机采样存在采样冗余问题，往往需要大量迭代才能收敛。

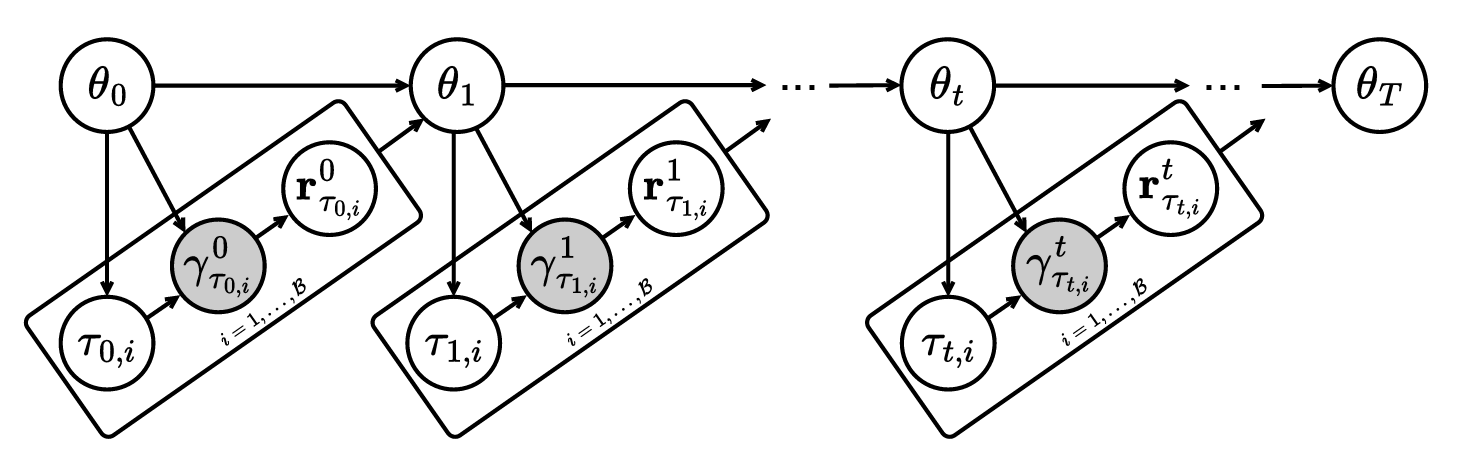
图 3：LLM 强化学习微调的概率图模型。奖励信号 $r_{{\tau }_{t,i}}^t$ 是一组对 $k$ 个生成响应进行评估的二值值，由潜在的成功率 ${\gamma }_{{\tau }_{t,i}}^t$ 所决定。提示批次 { τ t , i } i = 1 B \{\tau_{t,i}\}_{i=1}^{\mathcal{B}} {τt,i​}i=1B​ 是根据当前的 LLM ${\theta }_t$ 按照特定准则选取的。图中的白色节点表示观测变量，灰色节点表示潜在变量。

提示评估与选择的代价。 虽然在线提示选择可以提高样本效率，但通常会带来显著的计算开销，因为它通常需要在更大的候选集 ${\mathcal{T}}_t^{\hat{\mathcal{B}}}$（$\hat{\mathcal{B}}>\mathcal{B}$）上进行额外的真实评估，以对提示进行评分和筛选（Yu 等，2025；Bae 等，2025）：

Online Prompt Selection: T t B ^ → Evaluate { T t B ^ , R t B ^ } → Filter { T t B , R t B } . ( 8 ) \text{Online Prompt Selection:} \quad \mathcal{T}_t^{\hat{\mathcal{B}}} \xrightarrow{\text{Evaluate}} \{\mathcal{T}_t^{\hat{\mathcal{B}}},\mathcal{R}_t^{\hat{\mathcal{B}}} \}\xrightarrow{\text{Filter}} \{\mathcal{T}_t^{\mathcal{B}},\mathcal{R}_t^{\mathcal{B}} \}.\quad(8) Online Prompt Selection:TtB^​Evaluate ​{TtB^​,RtB^​}Filter ​{TtB​,RtB​}.(8)

形式上，提示选择的条件分布可以表示为：

$$p({\mathcal{T}}_t^{\mathcal{B}}\mid {\theta }_t)=\int p({\mathcal{T}}_t^{\mathcal{B}}\mid {\mathcal{R}}_t^{\hat{\mathcal{B}}},{\mathcal{T}}_t^{\hat{\mathcal{B}}})p({\mathcal{T}}_t^{\hat{\mathcal{B}}})\underset{\text{Extra Prompt Evaluation}}{\underbrace{\int p({\Gamma }_t^{\hat{\mathcal{B}}}\mid {\mathcal{T}}_t^{\hat{\mathcal{B}}},{\theta }_t)p({\mathcal{R}}_t^{\hat{\mathcal{B}}}\mid {\Gamma }_t^{\hat{\mathcal{B}}})d{\Gamma }_t^{\hat{\mathcal{B}}}}}d{\mathcal{R}}_t^{\hat{\mathcal{B}}}d{\mathcal{T}}_t^{\hat{\mathcal{B}}},(9)$$

其中，$p({\mathcal{T}}_t^{\hat{\mathcal{B}}})$ 表示采样一个更大候选集的概率，$p({\mathcal{T}}_t^{\mathcal{B}}\mid {\mathcal{R}}_t^{\hat{\mathcal{B}}},{\mathcal{T}}_t^{\hat{\mathcal{B}}})$ 指定了在某种准则下，在进行额外提示评估之后选出训练提示批次的条件概率。

从公式 (8) 和 (9) 可以看出，尽管这种“评估后筛选”的显式流程能够在线识别关键提示并加速学习，但对候选批次的额外推理评估会显著增加每一步的计算和内存开销。

3.2 面向提示成功率的贝叶斯推断

为避免额外的评估开销，我们借鉴了 MPTS（Wang 等，2025a）的思想，引入一个贝叶斯代理模型，用于：(i) 利用优化历史动态建模每个提示的成功率 ${\gamma }_{\tau }^t$；(ii) 实现无需额外 LLM 推理的基于后验引导的提示采样。

提示选择中的利用与探索： 提示选择的本质是从一组未知效果的提示中序贯地选择，并根据二值成功反馈动态估计它们的有效性。为了在利用已知高效提示与探索可能更具信息性的提示之间取得平衡，我们将在线提示选择建模为一个随机伯努利多臂老虎机问题（Bernoulli Bandit）。

定义 3.1（提示选择的伯努利老虎机建模）： 将每个提示 $\tau \in \mathcal{T}$ 视为一个“拉杆”，其特征为一个未知的成功率 ${\gamma }_{\tau }^t\in [0,1]$。每次“拉动拉杆”即对应于在当前策略 ${\pi }_{{\theta }_t}$下对提示 $\tau$ 进行一次查询，并观察其二值反馈 r τ t ∈ { 0 , 1 } r^t_\tau \in \{0, 1\} rτt​∈{0,1}，表示任务成功或失败。目标并非最大化累计奖励，而是优先选择那些能够为模型学习提供最具信息量梯度的提示，例如成功率 ${\gamma }_{\tau }^t\approx 0.5$（Bae 等，2025；Chen 等，2025）。

该建模方式为分析强化学习微调中的提示选择策略提供了一个统一的框架，并支持基于老虎机理论的原理化算法设计。以真实评估与确定性筛选为基础的先前方法，可以视为该框架的一个特例，对应于在几乎完全的候选反馈下进行贪婪利用。而本工作引入了一个贝叶斯模型，用于维护并更新每个 ${\gamma }_{\tau }^t$ 的后验分布，使得在无需昂贵 LLM 推理的前提下，也能实现高效的提示选择，并自然地在探索与利用之间取得平衡。

递归贝叶斯更新。 接下来，我们详细介绍用于高效后验推断的 ${\gamma }_{\tau }^t$ 递归贝叶斯更新过程。为了实现可解析的推断与闭式后验更新，我们为初始成功率引入一个 Beta 先验分布：

$${\gamma }_{\tau }^0\sim \mathrm{Beta}({\alpha }_{\tau }^0,{\beta }_{\tau }^0),(10)$$

其中，${\alpha }_{\tau }^0$ 和 ${\beta }_{\tau }^0$ 分别表示先验中对成功与失败的伪计数，通常设为 $(1,1)$ 以表示均匀先验。

根据贝叶斯公式，给定截至第 $t$ 步的观测数据，${\gamma }_{\tau }^t$ 的后验分布为：

$$\underset{\text{Updated Posterior}}{\underbrace{p({\gamma }_{\tau }^t\mid H_t)}}\propto \underset{\text{Likelihood}}{\underbrace{p(r_{\tau }^t\mid {\gamma }_{\tau }^t)}}\cdot \underset{\text{Conjugate Prior}}{\underbrace{p({\gamma }_{\tau }^t\mid H_{t-1})}},(11)$$

其中，$p({\gamma }_{\tau }^t\mid H_{t-1})\sim \mathrm{Beta}({\alpha }_{\tau }^t,{\beta }_{\tau }^t)$ 表示条件先验，它在 $t\ge 1$ 时使用上一次更新后的后验 $p({\gamma }_{\tau }^{t-1}\mid H_{t-1})$ 作为近似；而 $p(r_{\tau }^t\mid {\gamma }_{\tau }^t)$ 是在提示 $\tau$下观察到成功/失败的似然函数。

由于 Beta 分布与伯努利似然是共轭的（见公式 (1)），因此 $\gamma$ 的后验分布仍然服从 Beta 分布：

$${\gamma }_{\tau }^t\mid H_t\sim \mathrm{Beta}({\alpha }_{\tau }^{t^{\prime }},{\beta }_{\tau }^{t^{\prime }}),(12)$$

其递归更新规则如下所示：

$${\alpha }_{\tau }^{t^{\prime }}={\alpha }_{\tau }^t+s_{\tau }^t,{\beta }_{\tau }^{t^{\prime }}={\beta }_{\tau }^t+k-s_{\tau }^t.(13)$$

在流式贝叶斯设置下，这些将作为下一步的先验：

$${\alpha }_{\tau }^{t+1}={\alpha }_{\tau }^{t^{\prime }},{\beta }_{\tau }^{t+1}={\beta }_{\tau }^{t^{\prime }}.(14)$$

这些更新随着时间积累证据，其中 ${\alpha }_{\tau }^t$ 和 ${\beta }_{\tau }^t$ 分别表示截至第 $t$ 步为止，对提示 $\tau$ 观察到的成功与失败的总（伪）计数。该后验分布作为对提示难度不确定性的紧凑而高效的表示形式，支持后续的采样与决策过程，而无需调用 LLM 进行推理。

引入时间折扣机制。 需要注意的是，${\gamma }_{\tau }^t$ 的分布依赖于已更新的模型参数 ${\theta }_t$，若 ${\theta }_t$ 在迭代过程中发生显著变化，则会导致该分布变为非平稳。为了在此类情形下更准确地估计分布参数，我们对历史观测引入指数折扣策略，使近期反馈拥有更高的权重。设衰减因子 $\lambda \in (0,1)$，则第 $t$ 步参数后验的更新规则为：

$${\alpha }_{\tau }^{t^{\prime }}=\lambda \cdot {\alpha }_{\tau }^t+(1-\lambda )\cdot {\alpha }_{\tau }^0+s_{\tau }^t,{\beta }_{\tau }^{t^{\prime }}=\lambda \cdot {\beta }_{\tau }^t+(1-\lambda )\cdot {\beta }_{\tau }^0+k-s_{\tau }^t.(15)$$

这样的设计在动态训练过程中实现了适应性与稳定性之间的平衡。较小的 $\lambda$ 值会更加重视最近的反馈，有助于适应非平稳的训练动态；相反，当训练过程近似平稳时，将 $\lambda$ 设得更接近于 1 则能更好地利用历史数据，从而提升性能。关于该策略的消融研究见图 10。

后验估计的收敛性保证与效率提升。 我们引出定理 3.1，用于分析将后验均值作为真实时变成功率 ${\gamma }_{\tau }^t$ 的估计器时的误差上界。证明详见附录 B。

定理 3.1（有界成功率估计误差）。设第 $t$ 步训练时的后验均值估计为${\bar{\gamma }}_{\tau }^t:=\frac{{\alpha }_{\tau }^{t^{\prime }}}{{\alpha }_{\tau }^{t^{\prime }}+{\beta }_{\tau }^{t^{\prime }}}$，并假设真实成功率变化缓慢，即$|{\gamma }_{\tau }^t-{\gamma }_{\tau }^{t-1}|\le \delta ,\forall t$。则在至少 $1-2\exp (-2k{\eta }^2)$ 的概率下，该估计误差满足以下递推不等式：

$${ϵ}_t:=|{\bar{\gamma }}_{\tau }^t-{\gamma }_{\tau }^t|<\lambda \cdot ({ϵ}_{t-1}+\delta )+\frac{(1-\lambda )}{2}+\eta .$$

图 4：框架概览。左图：动态采样（Dynamic Sampling, Oracle）基于候选提示的实际 LLM 评估进行筛选，而我们的方法——模型预测提示选择（MoPPS）通过预测成功率来避免额外的推理开销。右图：MoPPS 基于后验参数预测候选提示的成功率，并选择最接近目标成功率 ${\gamma }^{\ast }$ 的提示用于训练；随后，利用新的反馈更新后验分布。

在高概率下，估计误差可以由前一轮误差 ${ϵ}_{t-1}$、变化幅度 $\delta$，以及由于有限采样次数 $k$ 引起的容差 $\eta$ 进行上界约束。该结果表明，后验分布能够提供对真实成功率的可靠且自适应的估计，从而实现无需额外 LLM 推理调用的有效提示选择。此外，该递推不等式还强调了衰减因子 $\lambda$ 的作用，它决定了历史反馈与近期反馈之间的重要性权衡。

我们进一步分析了 MoPPS 与 DS（Yu 等，2025）在计算复杂度方面的差异。DS 会不断地采样候选提示，调用 LLM 进行 rollouts，并筛除不满足预设约束的提示，直到选满 $\mathcal{B}$ 个提示。设 $p_{\text{keep}}$ 表示每个采样提示被保留的期望概率，$C_{\text{LLM}}$ 表示对每个提示生成并评估 $k$ 个 LLM rollouts 的期望计算成本，$C_{\text{pred}}$ 表示每个提示进行后验估计的成本。那么，在每一步中，提示选择与评估的期望时间复杂度为：

对于 DS：$\mathcal{O}\left(\lceil \frac{1}{p_{\text{keep}}}\rceil \cdot \mathcal{B}\cdot k\cdot C_{\text{LLM}}\right)$;

对于 MoPPS：

$$\mathcal{O}\left(\mathcal{B}\cdot C_{\text{pred}}+\mathcal{B}\cdot k\cdot C_{\text{LLM}}\right)\approx \mathcal{O}\left(\mathcal{B}\cdot k\cdot C_{\text{LLM}}\right)$$

由于通常 $p_{\text{keep}}<1$ 且 $C_{\text{pred}}\ll C_{\text{LLM}}$，MoPPS 通过避免在提示选择过程中反复调用 LLM 推理，相较于 DS 显著降低了计算开销。

3.3 模型预测提示选择（MoPPS）

图 1 的实证结果表明，后验分布对提示成功率的估计与真实成功率高度相关。这为使用后验分布作为高效代理评估提示难度提供了可靠基础，无需调用计算开销巨大的 LLM。以下介绍 MoPPS 的整体流程，包含两个关键步骤。

快速成功率估计来自近似后验： 我们不依赖于后验均值，而是采用 Thompson 采样（Thompson, 1933），从 Beta 后验分布中抽样，以在成功率估计中引入随机乐观性：

$${\hat{\gamma }}_{\tau }^t\sim \mathrm{Beta}({\alpha }_{\tau }^t,{\beta }_{\tau }^t)\forall \tau \in {\mathcal{T}}_t^{\hat{\mathcal{B}}}.(16)$$

请注意，此处的采样使用的是条件先验 $p({\gamma }_{\tau }^t\mid H_{t-1})$（见公式 (11)）作为后验 $p({\gamma }_{\tau }^t\mid H_t)$ 的代理，因为提示选择是在调用 LLM 之前进行的。这一设计使得提示选择过程无需推理调用，从而实现高效、免推理的选择机制。

重要的是，我们在这一工作中采用Thompson采样，因为它具有实现简单和对探索-利用的天然平衡，但是MoPPS可以很容易地兼容其他采样策略，如UCB。此外，我们的这种轻量化预测允许拓展${\mathcal{T}}_t^{\hat{\mathcal{B}}}$为整个提示池$\mathcal{T}$而几乎不增加任何开销，这对此前依赖真实评估的方法来说是不可能的。

从预测结果中进行主动提示选择。 已有研究（Bae 等，2025；Chen 等，2025）表明，中等难度的提示（即成功率接近某个目标值 ${\gamma }^{\ast }$，通常约为 $0.5$）在强化学习微调中能够提供最具信息量的梯度。基于这一发现，在每一步中，我们通过选择采样成功率 ${\hat{\gamma }}_{\tau }^t$ 最接近目标值 ${\gamma }^{\ast }$ 的 $\mathcal{B}$ 个提示，构建训练批次 ${\mathcal{T}}_t^{\mathcal{B}}$：

$${\mathcal{T}}_t^{\mathcal{B}}=Top-\mathcal{B}\left(\left\{\tau \in \mathcal{T}|-{\left||{\hat{\gamma }}_{\tau }^t-{\gamma }^{\ast }|\right|}_2^2\right\}\right),(17)$$

MoPPS还可以很容易的与其他筛选策略结合，如4.3.2节所示

3.4 实现流程

公式 (18) 概括了我们方法的核心思想，其中的 Predict 步骤强调用高效的基于后验的成功率预测替代昂贵的真实提示评估过程。

Model Predictive Prompt Selection: T t B ^ → Predict { T t B ^ , Γ ^ t B ^ } → Select { T t B } . ( 18 ) \text{Model Predictive Prompt Selection:} \quad \mathcal{T}_t^{\hat{\mathcal{B}}} \xrightarrow{\text{Predict}} \{\mathcal{T}_t^{\hat{\mathcal{B}}},\hat{\Gamma}_t^{\hat{\mathcal{B}}} \}\xrightarrow{\text{Select}} \{\mathcal{T}_t^{\mathcal{B}} \}. \quad(18) Model Predictive Prompt Selection:TtB^​Predict ​{TtB^​,Γ^tB^​}Select ​{TtB​}.(18)

该方法在保持计算效率的同时，鼓励探索，并保留了优先选择对学习最有益提示的能力。算法 1 展示了所提出的 MoPPS 方法，该方法可无缝集成到任何强化学习微调算法中。

4 实验

本节通过全面实验验证 MoPPS 在以下方面的有效性：能够准确在线预测提示难度，加速强化学习微调过程，并在性能上优于各类基线方法。进一步的分析还证实了该方法在多种选择策略下的灵活性、对先验知识的利用效果、在线后验更新的必要性，以及其与多种强化学习算法的兼容性。

4.1 实验设置

我们在三类具有代表性的推理任务上评估 MoPPS 的性能：数学、规划 ，以及多模态几何。为展示其通用性，我们采用了不同规模和类型的模型骨干，包括基础大语言模型、蒸馏变体以及多模态模型。在强化学习微调方面，我们使用广泛采用的 GRPO 算法，并基于 verl 框架（Sheng 等，2024）实现。

尽管如此，MoPPS 同样适用于其他算法，详见第 4.3.3 节。测试准确率通过每个问题生成 16 次独立响应，计算其 pass@1 的平均值，在训练曲线和评估结果中报告。更多实现细节见附录 C，附录 D 中包含消融实验，附录 E 提供数据示例等补充实验结果。

推理任务：

1. 数学推理： 我们在 MATH 数据集（Hendrycks 等，2021）的训练集上对大语言模型进行训练，该数据集包含来自数学竞赛的问题。按照先前工作（Luo 等，2025b），我们采用 DeepSeek-R1 蒸馏模型，包括 DeepSeek-R1-Distill-Qwen-1.5B 和 DeepSeek-R1-Distill-Qwen-7B（Guo 等，2025），并在训练过程中跟踪其在 AIME24 上的表现。最终评估则在多个基准上进行，包括 AIME24、AMC23、MATH500（Lightman 等，2023）、Minerva Math（Lewkowycz 等，2022）和 OlympiadBench（He 等，2024）。

2. 规划任务： 我们采用 Countdown 数字游戏任务，该任务要求使用基本的算术运算将给定的数字组合以接近目标值。训练在 Countdown-34 数据集（Pan 等，2025）的一个子集上进行，并在保留集上跟踪性能。最终评估在 Countdown-34（CD-34）及其更具挑战性的变体 Countdown-4（CD-4）上进行。我们使用的两个基础模型为 Qwen2.5-3B 和 Qwen2.5-7B（Yang 等，2024a），参考 Chen 等（2025）的方法设置。

3. 几何推理： 几何问题同时要求视觉理解与逻辑推理。我们使用两种视觉-语言模型：Qwen2.5-VL-3B-Instruct 和 Qwen2.5-VL-7B-Instruct（Bai 等，2025），在 Geometry3k 数据集（Lu 等，2021；Hiyouga，2025）的训练集上进行训练，并在其测试集上进行评估。

基线方法： 我们将 MoPPS 与两种常见的采样策略进行比较：(1).Uniform：从提示池中均匀随机采样训练提示；(2).Dynamic Sampling (DS):如公式 (6) 所述，过采样提示并基于其实际评估结果过滤掉无信息提示。需要注意的是，DS 依赖于真实评估反馈，因此可视为“Oracle”基线。我们的关注点在于相较于 DS 降低计算开销，而非在整体准确率上超越它。

4.2 主要结果

4.2.1 高相关性的难度预测

本工作的一个核心观点是：提示的难度（以当前策略下的成功率进行量化）可以在无需额外 LLM 推理的情况下动态预测。为了严格评估该预测的准确性，我们采用斯皮尔曼等级相关系数（Spearman’s rank correlation coefficient，Sedgwick, 2014）$\rho$ 作为评估指标。该指标通过计算两个序列排序后的皮尔逊相关系数（Cohen 等，2009），衡量它们之间的单调关系的强度与方向：

$$\rho =\frac{\mathrm{cov}(\mathrm{rank}({\hat{\Gamma }}^{\mathcal{B}}),\mathrm{rank}({\tilde{\Gamma }}^{\mathcal{B}}))}{{\sigma }_{\mathrm{rank}({\hat{\Gamma }}^{\mathcal{B}})}\cdot {\sigma }_{\mathrm{rank}({\tilde{\Gamma }}^{\mathcal{B}})}},(19)$$

其中，${\hat{\Gamma }}^{\mathcal{B}}={{\hat{\gamma }}_{\tau }}^{\mathcal{B}}$ 与 ${\tilde{\Gamma }}^{\mathcal{B}}={{\tilde{\gamma }}_{\tau }}^{\mathcal{B}}$ 分别表示预测的和经验估计的成功率，$\mathrm{rank}(\cdot )$ 表示对元素进行排序后的秩序值。为了评估统计显著性，我们报告在零假设（即 $\hat{\gamma }$ 与 $\tilde{\gamma }$相互独立）下的 $p$ 值；较低的 $p$ 值表示相关性越强。

在图 1 中，我们的方法在各类推理任务与不同骨干模型下均表现出稳定且显著的高秩相关性（$\rho >0.5$），同时对应的 $p$ 值极低。除此之外，可以清晰观察到训练过程中的趋势：相关性随时间逐步提升，最终稳定在较高水平。这一结果验证了我们所提出的贝叶斯代理模型能够随时间积累有效证据，并逐步优化其对提示难度的信念估计。

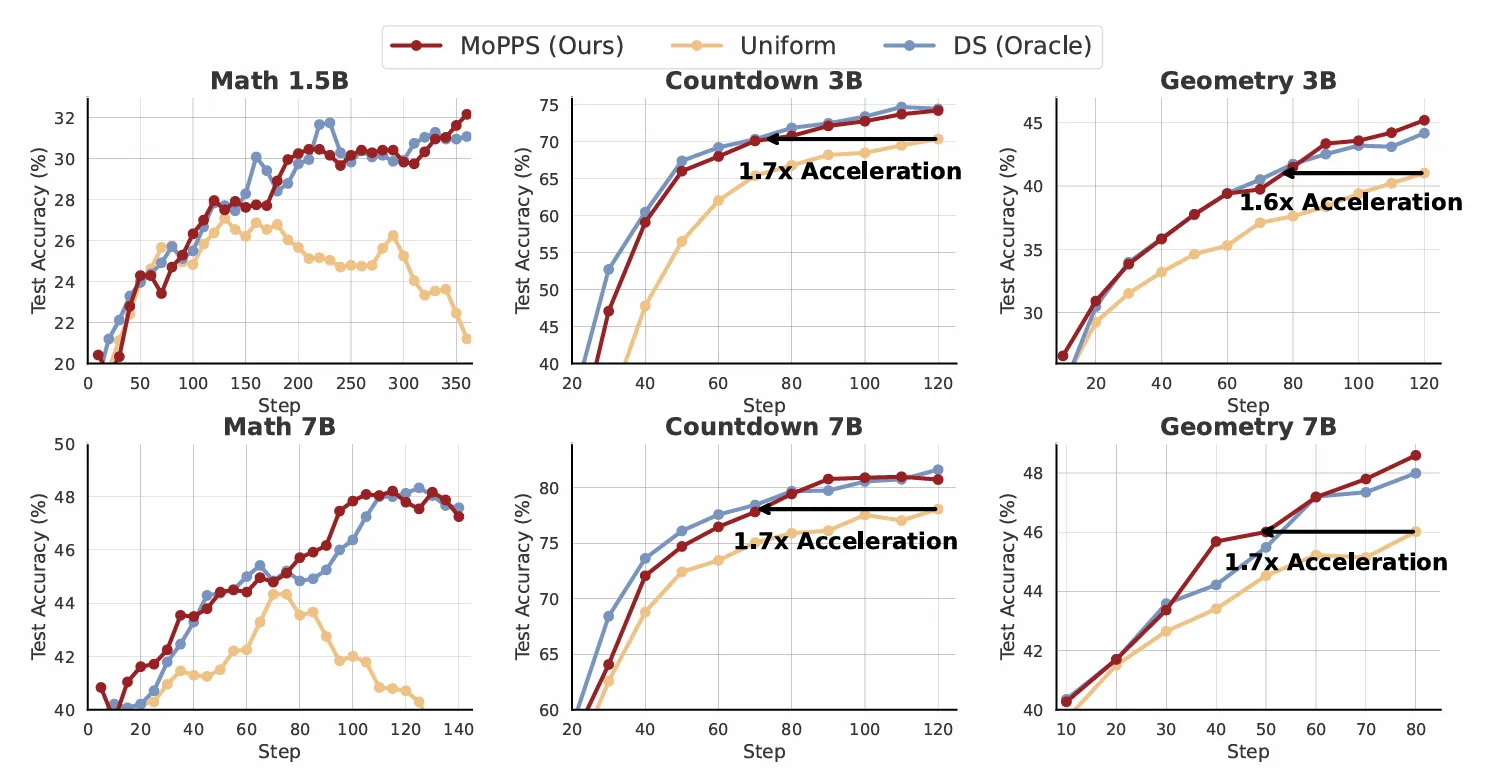
图 5：MoPPS 与基线方法在三类推理任务中、不同规模模型骨干下的训练曲线。值得注意的是，DS 作为 Oracle 基线依赖于代价高昂的精确 LLM 评估，并且需要显著更多的 rollouts。

4.2.2 加速的强化学习微调

我们在不同场景与模型骨干下比较了 MoPPS 与基线方法的训练表现。图 5 展示了训练曲线，表 1 总结了数学任务中的最终评估结果。得益于可靠的提示难度预测，所提出的 MoPPS 方法在训练速度和最终性能上均优于均匀提示选择方法。在 MATH 数据集上，Uniform 选择策略出现性能崩溃，可能是由于策略熵坍塌（entropy collapse, Liu 等，2025a）导致。而有效的在线提示选择方法能缓解此问题，保持训练进展稳定。

例如，MoPPS 在 AIME24 上相较于 Uniform 实现了约 $\frac{33.33-26.46}{26.46}\approx 26\%$ 的相对提升，在多个数学基准上（以 1.5B 模型为例）取得了平均约 $6.4\%$ 的相对提升。在 Countdown 与 Geometry 任务中，MoPPS 在各类模型规模下均表现出训练加速效果，最高接近 $1.8\times$的训练速度提升。

相比之下，MoPPS 在只使用约 $25\%$（MATH）和 $21\%$（Countdown）的 rollouts 情况下即可达到与 DS 相当的性能（见表 3）。这一效率提升得益于：DS 需要每步评估大量候选提示（高昂的 LLM 推理成本），而 MoPPS 通过后验采样有效摊销了该成本。

4.3 补充分析

4.3.1 先验知识与选择策略的影响

我们的方法默认采用均匀先验 $\text{Beta}(1,1)$ 和 $\text{Top-}\mathcal{B}$ 选择策略。为了验证方法的灵活性，我们评估了以下两种变体：

• (i) 替代的 “Threshold” 选择策略（参考 Bae 等，2025），该策略选择预测成功率落在固定区间 ${\gamma }_{min}\le {\hat{\gamma }}_{\tau }\le {\gamma }_{max}$ 内的提示进行采样；
• (ii) 融合先验知识：通过使用基础模型对所有提示进行预评估，并据此初始化 Beta 分布参数 { α , β } \{\alpha, \beta\} {α,β}。如图 6(a) 所示，这两种策略相较于均匀选择均表现出更优性能，其中 $\text{Top-}\mathcal{B}$ 表现最佳。此外，引入先验知识进一步提升了训练效率，并改善了最终性能（见表 1），尽管即使在没有先验的情况下，我们的方法仍然表现稳定有效。

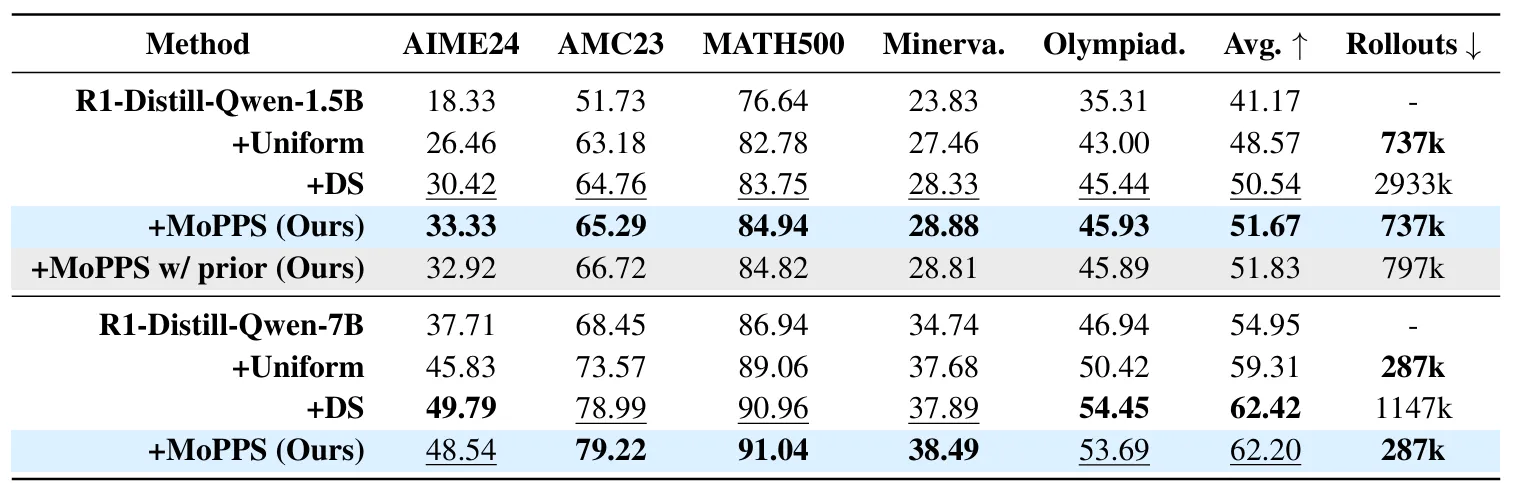
表 1：数学任务的评估结果。“Minerva.” 和 “Olympiad.” 分别指 Minerva Math 和 OlympiadBench；“+” 表示使用相应方法进行微调。准确率为每个问题独立生成 16 次响应后的 pass@1 平均值。“Avg.” 表示在所有基准测试上的平均准确率；“Rollouts” 表示微调过程中生成的样本总数。加粗表示最优结果，下划线表示次优结果。“MoPPS w/prior” 表示在 MoPPS 中融合了先验知识。

4.3.2 在线后验更新的作用

为评估在线后验更新的重要性，我们引入一个“离线”变体：该变体仅利用先验知识进行提示选择，在训练过程中不更新后验分布。如图 6(b) 所示，尽管该离线版本因初始先验较强在训练早期表现尚可，但在后期阶段准确率出现下降。这一下降的原因在于它无法适应策略的动态变化，导致提示难度估计逐渐失真，从而引发次优的提示选择。图 6© 进一步证实了这一现象：离线版本的秩相关性随着训练进行而逐步下降，而在线版本则能够通过不断引入新反馈更新后验分布，使得相关性持续上升、提示评估更为准确。

4.3.3 算法兼容性

我们在 Countdown 任务上将 MoPPS 集成到除 GRPO 外的两种强化学习算法中：PPO（Schulman 等，2017）和 Reinforce++（Hu，2025），以评估其算法兼容性。如表 2 和图 8 所示，无论底层强化学习算法为何，MoPPS 在训练效率与最终性能方面均显著优于均匀选择策略。这一结果表明，MoPPS 与具体算法无关（algorithm-agnostic），可以无缝集成到多种强化学习微调流程中，以提升采样效率。

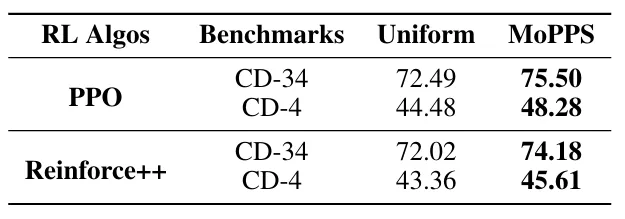
表 2：我们在 Countdown 任务上对比了 Uniform 与 MoPPS 在使用 PPO 和 Reinforce++ 两种算法下的表现。MoPPS 在 Countdown-34 和 Countdown-4 上均稳定实现了更高的 pass@1 准确率。

图 6：在 MATH 任务上使用 DeepSeek-R1-Distill-Qwen-1.5B 进行的消融实验，涉及选择策略、先验知识和在线后验更新。(a) 对比 $\text{Top-}\mathcal{B}$ 与 Threshold 选择策略，以及是否使用先验知识；(b) 离线选择策略（仅使用先验）与 MoPPS（结合先验与在线后验更新）的训练表现；© 离线变体与 MoPPS（含先验）在训练过程中的斯皮尔曼秩相关系数变化情况。

6 结论

本文提出了模型预测提示选择（Model Predictive Prompt Selection, MoPPS），一个轻量且高效的框架，用于通过自适应在线提示选择加速模型的强化学习微调过程。

在该方法中，我们将提示的成功率建模为潜在变量，并通过递归贝叶斯更新实现高效的提示难度预测，避免了额外的 LLM 推理，从而在训练过程中实现可靠且自适应的提示选择。

在数学、规划和几何等多种推理任务上的实验结果表明，MoPPS 在训练效率上显著优于均匀提示选择，并能达到或超越依赖评估的主流方法，同时大幅减少了 LLM rollout 成本。