问题描述:给定字符集C={x1,x2,…,xn}和每个字符频率f(xi),i=1,2,..,3,求关于C的一个最优前缀码。
·二元前缀码:表示一个字符的0,1字串不能是表示另一个字符的0,1字串的前缀。
·B=∑f(xi)d(xi)是存储一个字符的平均值。d(xi)为码长。
·平均码长达到最小的前缀编码方案称为字符集C的一个最优前缀编码。
·例:字符集及其频率如
表.长为100000的文件:
·定长码:300000 bit,
·变长码:224000 ,省25%
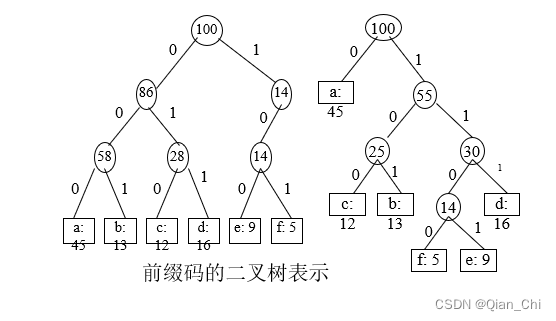
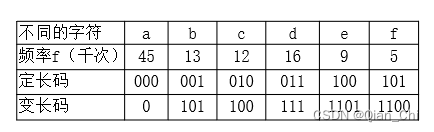
伪代码:
贪心算法是Huffman编码: Huffman(C)
·1.n:=|C|
·2.Q:=C //按频率构造min堆
·3.for i=1 to n-1 do
·4. z:=Allocate-node() //生成树节点z
·5. z.left:=Q中最小元x
·6. z.right:= Q中最小元y
·7. f(z):=f(x)+f(y)
·8. insert(Q,z) //将z插入Q并保持递增
·9 end for
·10. return z //树z从根到叶子的路径即为叶子字符的编码
实现:
//算法4.4 最优前缀码问题(哈夫曼算法) Huffman(C)
//输入:C={x1,x2,...,xn}是字符集,每个字符频率f(xi),i=1,2,...,n
//输出:Q
#include<stdio.h>
#include<string.h>
struct Huffman {
int weight;//权值
char ch;//字符
int parent;//父亲节点
int left;//左孩子
int right;//右孩子
};
struct Hcode {
int code[100];//字符的哈夫曼编码的存储
int start;//开始位置
};
struct Huffman huffman[100];//最大字符编码数组长度
struct Hcode code[100];//最大哈夫曼编码结构体数组的个数
void Huffman(char* C, int Q[]) {
int n = strlen(C);
int i, j;
for (i = 0; i < n; i++) {
huffman[i].ch = C[i];
}
for (i = 0; i < n * 2 - 1; i++) {//哈夫曼节点的初始化
huffman[i].weight = 0;
huffman[i].parent = -1;
huffman[i].left = -1;
huffman[i].right = -1;
}
//赋权重
for (i = 0; i < n; i++) {
huffman[i].weight = Q[i];
// printf("%d\n",huffman[i].weight);
}
//每次找出权重最小的节点,生成新的节点,需要n-1次合并
int a, b, w1, w2;
for (i = 0; i < n - 1; i++) {
a = b = -1;
w1 = w2 = 10000;
for (j = 0; j < n + i; j++) { //注意每次在n+i里面遍历
//得到权重最小的点
if (huffman[j].parent == -1 && huffman[j].weight < w1) {//如果每次最小的更新了,那么需要把上次最小的给第二个最小的
w2 = w1;
b = a;
a = j;
w1 = huffman[j].weight;
}
//注意这里用else if而不是if,是因为它们每次只选1个就可以了
else if (huffman[j].parent == -1 && huffman[j].weight < w2) {
b = j;
w2 = huffman[j].weight;
}
}
//每次找到最小的两个节点后要记得合并成一个新的节点
huffman[n + i].left = a;
huffman[n + i].right = b;
huffman[n + i].weight = w1 + w2;
huffman[a].parent = n + i;
huffman[b].parent = n + i;
}
}
//打印每个字符的哈夫曼编码
void PrintHuffmanTree(int n) {
struct Hcode CurrentCode; //保存当前叶子节点的字符编码
int CurrentParent; //当前父节点
int c; //下标和叶子节点的编号
int i, j;
for (i = 0; i < n; i++) {
CurrentCode.start = n - 1;
c = i;
CurrentParent = huffman[i].parent;
//父节点不等于-1才可以遍历
while (CurrentParent != -1) {
//判断当前父节点的左孩子是否为当前值,是则取0,否则取1
if (huffman[CurrentParent].left == c) {
CurrentCode.code[CurrentCode.start] = 0;
}
else {
CurrentCode.code[CurrentCode.start] = 1;
}
CurrentCode.start--;
c = CurrentParent;//保存当前变量i
CurrentParent = huffman[c].parent;
}
//把当前叶子节点信息保存到编码结构体里面
for (j = CurrentCode.start + 1; j < n; j++) {
code[i].code[j] = CurrentCode.code[j];
}
code[i].start = CurrentCode.start;
}
}
int main() {
int n = 0, i, j;
char C[] = { 'a','b','c','d','e','f','\0' };
int Q[] = { 45,13,12,16,9,5};
n = strlen(C);
Huffman(C, Q);
PrintHuffmanTree(n);
for (i = 0; i < n; ++i) {
printf("字符%c的哈夫曼编码为:", huffman[i].ch);
for (j = code[i].start + 1; j < n; ++j) {
printf("%d", code[i].code[j]);
}
printf("\n");
}
return 0;
}
运行结果:
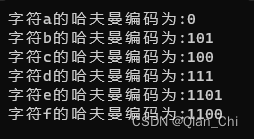




 文章讲述了如何使用贪心算法实现Huffman编码,一种构建最优前缀码的方法,通过计算字符频率并构造哈夫曼树来压缩数据,降低存储成本。文中给出了详细步骤和C语言代码示例。
文章讲述了如何使用贪心算法实现Huffman编码,一种构建最优前缀码的方法,通过计算字符频率并构造哈夫曼树来压缩数据,降低存储成本。文中给出了详细步骤和C语言代码示例。
















 1807
1807

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








