数学问题总结

给出三点求外接圆圆心、半径

double a = ((y2 - y1) * (y3 * y3 - y1 * y1 + x3 * x3 - x1 * x1) - (y3 - y1) * (y2 * y2 - y1 * y1 + x2 * x2 - x1 * x1)) / (2.0 * ((x3 - x1) * (y2 - y1) - (x2 - x1) * (y3 - y1)));
double b = ((x2 - x1) * (x3 * x3 - x1 * x1 + y3 * y3 - y1 * y1) - (x3 - x1) * (x2 * x2 - x1 * x1 + y2 * y2 - y1 * y1)) / (2.0 * ((y3 - y1) * (x2 - x1) - (y2 - y1) * (x3 - x1)));
double r2 = (x1 - a) * (x1 - a) + (y1 - b) * (y1 - b);

---

质数

bool isPrime(int n) {	//返回1表示判断为质数，0为非质数
	float n_sqrt;
	if (n == 2 || n == 3) return true;
	if (n % 6 != 1 && n % 6 != 5) return false;
	n_sqrt = floor(sqrt((float)n));
	for (int i = 5; i <= n_sqrt; i += 6) {
		if (n % (i) == 0 | n % (i + 2) == 0) return false;
	}
	return true;
}

---

唯一分解定理

#include<bits/stdc++.h>
#define ll long long
using namespace std;

// 唯一分解定理 
// prime_factors()；将n分解成质因子的积的形式（相同的用指数表示）
// first:底数，second:指数
vector<pair<ll, int>> prime_factors(ll n) {
	vector<pair<ll, int>> f;
	int k = sqrt(n) + 1;
	ll p;	int q;
	for (ll i = 2; i <= k; ++i) {
		q = 0;		if (n % i == 0)	p = i;
		while (n % i == 0)	++q, n /= i;
		if (p)	f.push_back(make_pair(p, q));
	}
	if (n > 1)	f.push_back(make_pair(n, 1));
	return f;
}

---

日期转换

int getId(int y, int m, int d) {
	if (m < 3) { y--; m += 12; }
	return 365 * y + y / 4 - y / 100 + y / 400 + (153 * (m - 3) + 2) / 5 + d - 307;
}
vector<int> date(int id) {
	int x = id + 1789995, n, i, j, y, m, d;
	n = 4 * x / 146097;
	x -= (146097 * n + 3) / 4;
	i = (4000 * (x + 1)) / 1461001; x -= 1461 * i / 4 - 31;
	j = 80 * x / 2447; d = x - 2447 * j / 80; x = j / 11;
	m = j + 2 - 12 * x; y = 100 * (n - 49) + i + x;
	return vector<int>({ y, m, d });
}

组合数

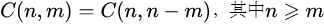
auto Cnm = [](long long n, long long m) -> long long {
    m = min(m, n - m); // C(n, m) == C(n, n - m) = {n ... (n-m+1)} / {m!}
    long long ans = 1;
    for(int x = n - m + 1, y = 1; y <= m; ++x, ++y) 
        ans = ans * x / y;
    return ans;
};