机器学习：线性模型（python）

查易天

于 2025-02-22 15:20:31 发布

阅读量153

点赞数 2

文章标签：机器学习 python

本文链接：https://blog.youkuaiyun.com/QQqq728802307/article/details/145795451

版权

一元线性回归模型

先导入所需要使用的包

######   导入库   ######
import numpy as np
import matplotlib.pyplot as plt

设置一元线性回归模型

######   函数   ######
def simple_linear_regression(x,y):
    '''
    一元线性回归

    参数：
    x(numpy.ndarray) ：自变量，形状为 (n,)
    y(numpy.ndarray) ：因变量，形状为 (n,)

    返回:
    x_mean : x均值
    y_mean : y均值
    beta_0 (float) : 截距
    beta_1 (float) : 斜率
    y_pred : 拟合值
    MSE : 均方误差
    '''

    # 计算均值
    x_mean=np.mean(x)
    y_mean=np.mean(y)

    # 计算斜率beta_1
    numerator = np.sum((x-x_mean)*(y-y_mean)) # 分子
    denominator = np.sum((x-x_mean)**2) # 分母
    if denominator == 0: # 分母为0进行提示
        raise ValueError("分母不能为0")
    beta_1 = numerator / denominator

    # 计算截距beta_0
    beta_0 = y_mean - beta_1*x_mean
    
    # 拟合函数(预测)
    def predict(x,beta_0,beta_1):
        return beta_0+beta_1*x
    y_pred = predict(x,beta_0,beta_1) # 拟合值，即y的预测值

    # 均方误差函数
    def mean_squared_error(y, y_pred):
        return np.mean((y-y_pred)**2)
    MSE=mean_squared_error(y, y_pred) # 均方误差

    return x_mean,y_mean,beta_0,beta_1,y_pred,MSE

举例运行

######   导入/生成数据   ######
# 一元线性回归数据
#x=[1,2,3,4,5,6,7]
#y=[7,2,5,8,4,6,3]
# 生成示例数据
np.random.seed(42) # 使用 NumPy 库中的随机数生成器，并设置了随机种子为 42，这样每次生成的序列都相同
x=np.linspace(0,10,100) # 生成了一个包含 100 个元素的一维数组，这些元素均匀分布在 0 到 10 的区间内
y=2*x+1+np.random.randn(100) # y与x有一定的线性关系，同时还包括一定的随机扰动

######   主程序   ######
# 创建 LinearRegression 类的实例
lr=LinearRegression()
x_mean,y_mean,beta_0,beta_1,y_pred,MSE=lr.simple_linear_regression(x,y) # 调用一元线性回归函数
#print(f"自变量均值 x_mean：{x_mean}") # 输出自变量均值
#print(f"因变量均值 y_mean：{y_mean}") # 输出因变量均值
#print(f"斜率 beta_1: {beta_1}") # 输出斜率
#print(f"截距 beta_0: {beta_0}") # 输出截距
print(f"均方误差 MSE: {MSE}") # 输出均方误差

# 绘制原始数据与拟合直线
plt.scatter(x,y,label="Original data",color='blue') # 设置横纵坐标数据、图例及其对应颜色
plt.plot(x,y_pred,label="Fitted line",color='red') # 设置拟合直线对应的数据、标签以及对应颜色
#plt.axvline(x=x_mean, color='green', linestyle='--', label=f'x_mean: {x_mean:.2f}') # 设置自变量均值线
#plt.axhline(y=y_mean, color='orange', linestyle='--', label=f'y_mean: {y_mean:.2f}') # 设置因变量均值线
plt.xlabel('x') # 设置横轴名称
plt.ylabel('y') # 设置纵轴名称
plt.legend() # 在图表中添加图例，通过一些参数可以自定义图例的位置和样式，这里默认图例设置
#plt.legend(loc='upper left', bbox_to_anchor=(1, 1)) # 将图例放在图表外不遮挡数据的位置
plt.title('Simple Linear Regression Model') # 设置图像名称
plt.show() # 做图

输出结果如下：

均方误差 MSE: 0.8149047134980782

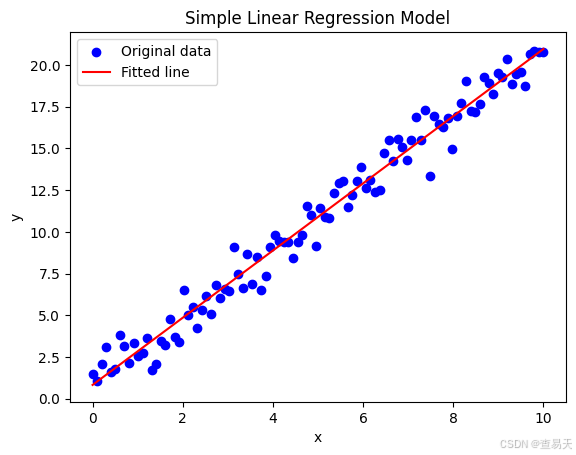
多元线性回归模型

使用的包仅包括numpy

impor numpy as np
def multiple_linear_regression(X, y):
    """
    多元线性回归

    参数:
    X: 自变量矩阵，形状为 (n, p) 的 numpy 数组，n 为样本数，p 为特征数
    y: 因变量，形状为 (n,) 的 numpy 数组

    返回：
    回归系数
    """

    # 在 X 矩阵前添加一列全为 1 的列，用于拟合截距
    X_beta_0 = np.c_[np.ones((X.shape[0], 1)), X]
    print(f"X_beta_0 形状: {X_beta_0.shape}")

        # 使用正规方程求解回归系数
    try:
        # 检查矩阵是否可逆
        np.linalg.inv(X_beta_0.T.dot(X_beta_0))
        self.beta = np.linalg.inv(X_beta_0.T.dot(X_beta_0)).dot(X_beta_0.T).dot(y)
    except np.linalg.LinAlgError:
        print("矩阵不可逆，无法使用正规方程求解。")
        self.beta = np.linalg.pinv(X_beta_0).dot(y)

    # 多元线性回归的 拟合函数(预测)
    X_beta_0 = np.c_[np.ones((X.shape[0], 1)), X]
    y_pred = X_beta_0.dot(self.beta)
        
    # 多元线性回归的 均方误差函数
    MSE = np.mean((y - y_pred) ** 2)

    return self.beta,y_pred,MSE

举例运行

######   导入/生成数据   ######
# 多元线性回归数据
np.random.seed(42)
X_multi = np.random.rand(100, 3)
y_multi = 1 + 2 * X_multi[:, 0] + 3 * X_multi[:, 1] + 4 * X_multi[:, 2] + np.random.randn(100)

######   主程序   ######
# 创建 LinearRegression 类的实例
lr = LinearRegression()
coefficients, y_pred, MSE = lr.multiple_linear_regression(X_multi, y_multi) # 调用多元线性回归函数
if coefficients is not None:
    print(f"回归系数: {coefficients}")
    print(f"预测值示例（前 5 个）: {y_pred[:5]}")
    print(f"均方误差 MSE: {MSE}")

输出结果如下：

X_beta_0 形状: (100, 4)

回归系数: [0.73501456 2.27800411 2.84223781 4.57040576]

预测值示例（前 5 个）: [7.63588396 3.25516138 6.07654736 6.8393944 4.06585444]

均方误差 MSE: 0.9203988206421478

集中到一个类中

######   导入库   ######
import numpy as np
import matplotlib.pyplot as plt

######   函数   ######
class LinearRegression():
    def __init__(self):
        self.beta = None

    def simple_linear_regression(self,x,y):
        '''
        一元线性回归

        参数：
        x(numpy.ndarray) ：自变量，形状为 (n,)
        y(numpy.ndarray) ：因变量，形状为 (n,)

        返回:
        x_mean : x均值
        y_mean : y均值
        beta_0 (float) : 截距
        beta_1 (float) : 斜率
        y_pred : 拟合值
        MSE : 均方误差
        '''

        # 计算均值
        x_mean=np.mean(x)
        y_mean=np.mean(y)

        # 计算斜率beta_1
        numerator = np.sum((x-x_mean)*(y-y_mean)) # 分子
        denominator = np.sum((x-x_mean)**2) # 分母
        if denominator == 0: # 分母为0进行提示
            raise ValueError("分母不能为0")
        beta_1 = numerator / denominator

        # 计算截距beta_0
        beta_0 = y_mean - beta_1*x_mean
        
        # 拟合函数(预测)
        def predict(x,beta_0,beta_1):
            return beta_0+beta_1*x
        y_pred = predict(x,beta_0,beta_1) # 拟合值，即y的预测值

        # 均方误差函数
        def mean_squared_error(y, y_pred):
            return np.mean((y-y_pred)**2)
        MSE=mean_squared_error(y, y_pred) # 均方误差

        return x_mean,y_mean,beta_0,beta_1,y_pred,MSE

    def multiple_linear_regression(self, X, y):
        """
        多元线性回归

        参数:
        X: 自变量矩阵，形状为 (n, p) 的 numpy 数组，n 为样本数，p 为特征数
        y: 因变量，形状为 (n,) 的 numpy 数组

        返回：
        回归系数
        """

        # 在 X 矩阵前添加一列全为 1 的列，用于拟合截距
        X_beta_0 = np.c_[np.ones((X.shape[0], 1)), X]
        print(f"X_beta_0 形状: {X_beta_0.shape}")

         # 使用正规方程求解回归系数
        try:
            # 检查矩阵是否可逆
            np.linalg.inv(X_beta_0.T.dot(X_beta_0))
            self.beta = np.linalg.inv(X_beta_0.T.dot(X_beta_0)).dot(X_beta_0.T).dot(y)
        except np.linalg.LinAlgError:
            print("矩阵不可逆，无法使用正规方程求解。")
            self.beta = np.linalg.pinv(X_beta_0).dot(y)
    
        # 多元线性回归的 拟合函数(预测)
        X_beta_0 = np.c_[np.ones((X.shape[0], 1)), X]
        y_pred = X_beta_0.dot(self.beta)
            
        # 多元线性回归的 均方误差函数
        MSE = np.mean((y - y_pred) ** 2)

        return self.beta,y_pred,MSE


'''      一元线性回归
######   导入/生成数据   ######
# 一元线性回归数据
#x=[1,2,3,4,5,6,7]
#y=[7,2,5,8,4,6,3]
# 生成示例数据
np.random.seed(42) # 使用 NumPy 库中的随机数生成器，并设置了随机种子为 42，这样每次生成的序列都相同
x=np.linspace(0,10,100) # 生成了一个包含 100 个元素的一维数组，这些元素均匀分布在 0 到 10 的区间内
y=2*x+1+np.random.randn(100) # y与x有一定的线性关系，同时还包括一定的随机扰动

######   主程序   ######
# 创建 LinearRegression 类的实例
lr=LinearRegression()
x_mean,y_mean,beta_0,beta_1,y_pred,MSE=lr.simple_linear_regression(x,y) # 调用一元线性回归函数
#print(f"自变量均值 x_mean：{x_mean}") # 输出自变量均值
#print(f"因变量均值 y_mean：{y_mean}") # 输出因变量均值
#print(f"斜率 beta_1: {beta_1}") # 输出斜率
#print(f"截距 beta_0: {beta_0}") # 输出截距
print(f"均方误差 MSE: {MSE}") # 输出均方误差

# 绘制原始数据与拟合直线
plt.scatter(x,y,label="Original data",color='blue') # 设置横纵坐标数据、图例及其对应颜色
plt.plot(x,y_pred,label="Fitted line",color='red') # 设置拟合直线对应的数据、标签以及对应颜色
#plt.axvline(x=x_mean, color='green', linestyle='--', label=f'x_mean: {x_mean:.2f}') # 设置自变量均值线
#plt.axhline(y=y_mean, color='orange', linestyle='--', label=f'y_mean: {y_mean:.2f}') # 设置因变量均值线
plt.xlabel('x') # 设置横轴名称
plt.ylabel('y') # 设置纵轴名称
plt.legend() # 在图表中添加图例，通过一些参数可以自定义图例的位置和样式，这里默认图例设置
#plt.legend(loc='upper left', bbox_to_anchor=(1, 1)) # 将图例放在图表外不遮挡数据的位置
plt.title('Simple Linear Regression Model') # 设置图像名称
plt.show() # 做图
'''

'''      多元线性回归
######   导入/生成数据   ######
# 多元线性回归数据
np.random.seed(42)
X_multi = np.random.rand(100, 3)
y_multi = 1 + 2 * X_multi[:, 0] + 3 * X_multi[:, 1] + 4 * X_multi[:, 2] + np.random.randn(100)

######   主程序   ######
# 创建 LinearRegression 类的实例
lr = LinearRegression()
coefficients, y_pred, MSE = lr.multiple_linear_regression(X_multi, y_multi) # 调用多元线性回归函数
if coefficients is not None:
    print(f"回归系数: {coefficients}")
    print(f"预测值示例（前 5 个）: {y_pred[:5]}")
    print(f"均方误差 MSE: {MSE}")
'''