多重背包问题【最终优化版】

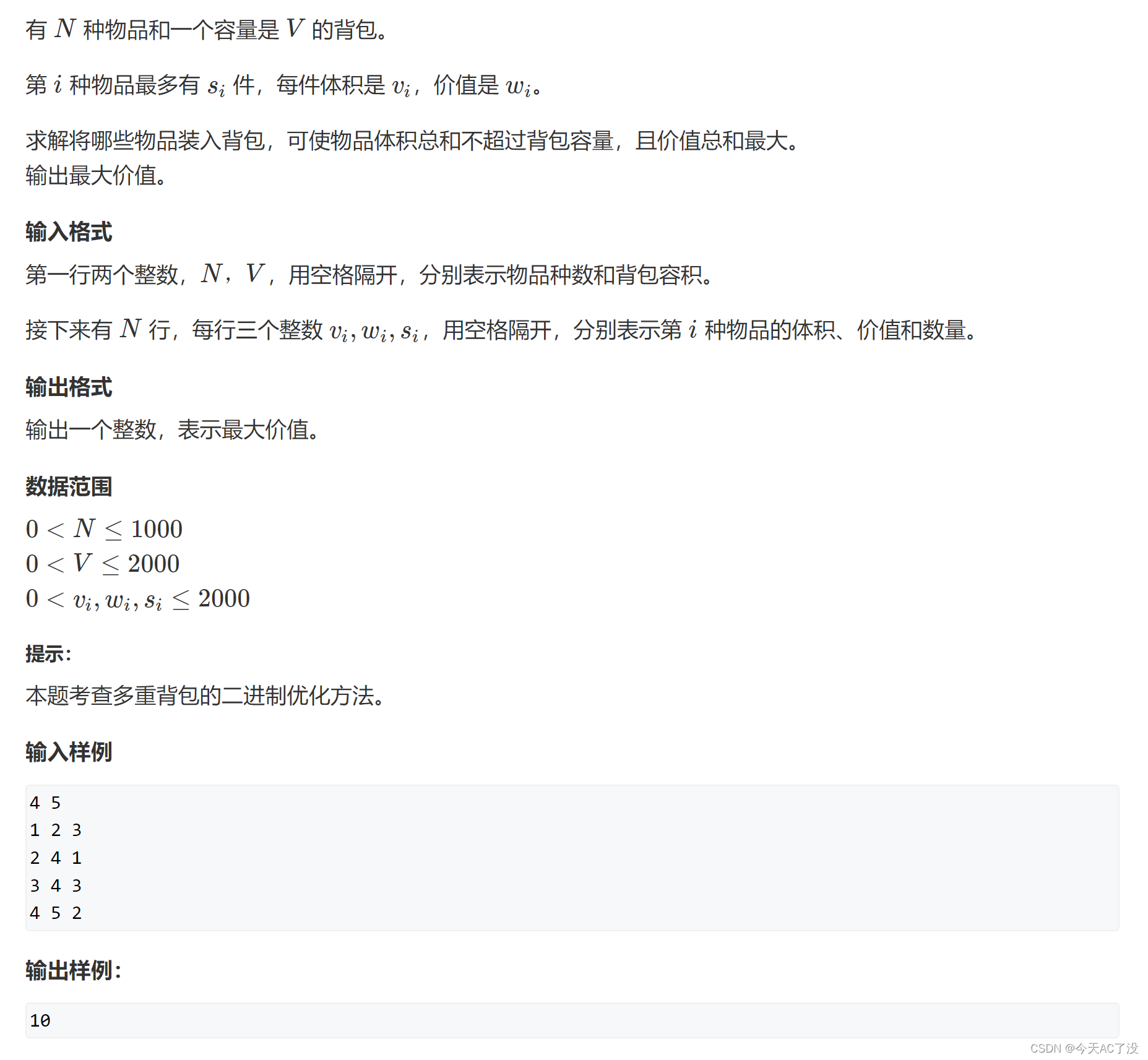
分析

1、打包思想，

可以将s个i物品，打包成log s 个新的物品堆，一堆一堆的，通过每一堆的数，都能够拼出0~s的任何一个数，

例如，s：0~1023 ，那么我们就分为10堆 分别为 1/2/4/8/16/32/64/128/256/512

可以通过每堆都可以拼出0~1023的每一个数，

 2、思路怎么想的？

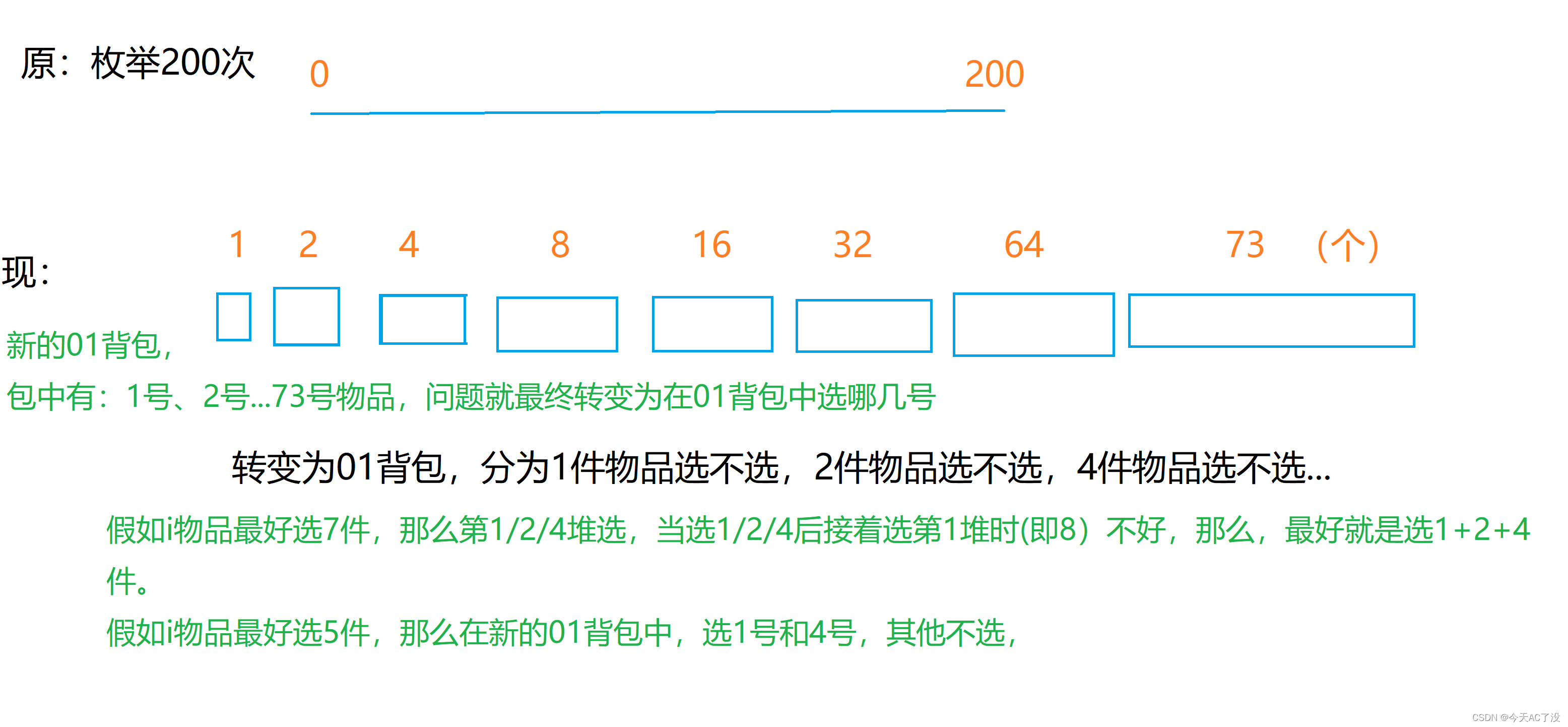
 3、代码怎么写？

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 25000 ;//为什么开25000，是因为 2000 * log2000 = 21000

int v[N] , w[N];
int n,m;
int f[N];//一维01背包优化

int main()
{
    cin>>n>>m;
    int cnt = 0;//分组的组别，即几号
    
    
    //1、预处理，枚举每一个物品，按二进制分组
    for( int i = 1 ; i<=n ; i++ )
    {
        int a , b , s;
        cin>>a>>b>>s;
        //1.分组
        int k = 1;//组别里面的个数1/2/4/8/16/...
        while(k <= s)
        {
            cnt ++;
            v[cnt] = a * k;//更新v和w，打包在一起
            w[cnt] = b * k;
            s -= k;//s减小
            k *= 2;//更新k
        }
        //2.剩余一组
        if(s > 0)
        {
            cnt ++;
            v[cnt] = a * s;
            w[cnt] = b * s;
        }
    }
    
    //2、01背包问题求解
    n = cnt;//枚举次数正式由个数变成组别数
    for( int i = 1; i <= n ; i++ )
        for( int j = m ; j >= v[i] ; j-- )
            f[j] = max( f[j] , f[j - v[i]] + w[i] );
    cout<<f[m]<<endl;
    return 0;
}
//把自己菜哭了~

 思绪逆着时光在向后倒退，退回流逝的岁月，退到当年，退到那片绿色的草原和那些个红霞艳艳的傍晚...... 

                                    ---《平凡的世界》 第四十七章