信息安全数学基础知识汇总，零基础入门到精通，收藏这篇就够了

一、整除

1、整除的概念

整除的概念
∀a,b∈Z,且b≠0,如果存在一个整数q,使得a=qb成立,则称为b整除a,或者a被b整除,记作b∣a\forall a,b\in Z,且b\neq 0,如果存在一个整数q,使得a=qb成立,则称为b整除a,或者a被b整除,记作b|a∀a,b∈Z,且b=0,如果存在一个整数q,使得a=qb成立,则称为b整除a,或者a被b整除,记作b∣a

整除的性质：
若c∣a，c∣b，那么c∣sa+tb(s,t∈Z)若c|a，c|b，那么c|sa+tb(s,t\in Z)若c∣a，c∣b，那么c∣sa+tb(s,t∈Z)

素数的性质：
若n是一个正合数，p是n的一个大于1的最小正因数，那么p一定是素数若n是一个正合数，p是n的一个大于1的最小正因数，那么p一定是素数若n是一个正合数，p是n的一个大于1的最小正因数，那么p一定是素数
素数有无穷多个（可以用迭代法证明N=p1p2p3…pn+1，其中N一定为素数）素数有无穷多个（可以用迭代法证明N=p_1p_2p_3…p_n+1，其中N一定为素数）素数有无穷多个（可以用迭代法证明N=p1​p2​p3​…pn​+1，其中N一定为素数）

2、Euclid算法

带余整除法（Euclid除法）
∀a,b∈Z,b>0,一定存在唯一整数q,r,使得a=qb+r(0≤r<b)\forall a,b\in Z,b\gt 0,一定存在唯一整数q,r,使得a=qb+r(0\le r\lt b)∀a,b∈Z,b>0,一定存在唯一整数q,r,使得a=qb+r(0≤r<b)
用数轴即可证明

带余整除法推论：
说白了就是辗转相除法计算最大公约数
(a,b)=(b,r)=…=(r0,0)(a,b) = (b,r) = … = (r_0, 0)(a,b)=(b,r)=…=(r0​,0)
用整除法即可证明

最大公约数可写成gcd(a,b)

最大公约数的性质：
存在不全为0的a、b，若d为a和b的最大公约数，那么d一定是{sa+tb∣s,t∈Z}中最小的正整数存在不全为0的a、b，若d为a和b的最大公约数，那么d一定是\{sa+tb|s,t\in Z\}中最小的正整数存在不全为0的a、b，若d为a和b的最大公约数，那么d一定是{sa+tb∣s,t∈Z}中最小的正整数

3、扩展的Eculid算法

求sa+tb = （a，b）
用辗转相除法计算出最大公约数，再用最大公约数求a和b的系数s和t

可以用来求a模m的逆元：
若(a,m)=1(a,m)=1(a,m)=1，那么sa+tm=1sa+tm=1sa+tm=1，因为tm模m是0，所以s就是a的逆元

4、算术基本定理

有a、b、c，其中b、c不为0，如果（a,c）=1，那么（ab,c）=（b,c）有a、b、c，其中b、c不为0，如果（a,c） = 1，那么（ab,c） = （b,c）有a、b、c，其中b、c不为0，如果（a,c）=1，那么（ab,c）=（b,c）

[a,b]=ab/(a,b)[a,b] = ab/(a,b)[a,b]=ab/(a,b)
用整数的标准分解式可以证明，即素数的n次方的乘积形式，最大公约数的指数是最大的，最小公倍数的指数是最小的

算术基本定理：
任一整数n>1都可以表示成素数的乘积，且在不考虑素数的顺序情况下，该表达式是唯一的
N=p1p2…pnN=p_1p_2…p_nN=p1​p2​…pn​

二、同余

1、同余和同余类

同余定理
设m是一个正整数，a，b是两个整数，则a≡b mod ma\equiv b\ mod\ ma≡b mod m，且充要条件是a=b+km / (m∣a−b)a=b+km\ /\ (m|a-b)a=b+km / (m∣a−b)

同余是一个等价关系，满足自反性、对称性、传递性

定理1：
若m为一个正整数，a，b，c，d是四个整数，如果a≡b mod ma\equiv b\ mod\ ma≡b mod m且c≡d mod mc\equiv d\ mod\ mc≡d mod m，则有a+c≡b+d mod ma+c\equiv b+d\ mod\ ma+c≡b+d mod m、ac≡bd mod mac\equiv bd\ mod\ mac≡bd mod m、an≡bn mod ma^n\equiv b^n\ mod\ man≡bn mod m
证明第二个：
m∣(a−b)c+(c−d)bm|(a-b)c+(c-d)bm∣(a−b)c+(c−d)b即可证明
第三个同理

定理2：
若m为正整数，a≡b mod ma\equiv b\ mod\ ma≡b mod m，d∣(a,b,m)d|(a,b,m)d∣(a,b,m)，那么ad≡bd mod md\frac{a}{d}\equiv\frac{b}{d}\ mod\ \frac{m}{d}da​≡db​ mod dm​
若m为正整数，a≡b mod ma\equiv b\ mod\ ma≡b mod m，d∣md|md∣m，那么a≡b mod da\equiv b\ mod\ da≡b mod d

定理3：
若ak≡bk mod mak\equiv bk\ mod\ mak≡bk mod m，那么a≡b mod m(k,m)a\equiv b\ mod\ \frac{m}{(k,m)}a≡b mod (k,m)m​
证明：
由条件可得m∣(a,b)km|(a,b)km∣(a,b)k，得(a−b)k=qm(a-b)k=qm(a−b)k=qm，再同时除以(k,m)(k,m)(k,m)，证毕

定理4：
设m是正整数，整数a满足(a,m)=1(a,m)=1(a,m)=1，b是任意整数。若x遍历模m的一个完全剩余系，则ax+bax+bax+b也遍历模m的一个完全剩余系

逆元：
设m是一个正整数，a是一个整数，如果存在整数b使得ab≡1 mod mab\equiv 1\ mod\ mab≡1 mod m成立，则b是a的逆元

模m的剩余类：
Zm={0‾,1‾,…,m−1‾}Z_m=\{\overline0,\overline1,…,\overline{m-1}\}Zm​={0,1,…,m−1​}
关于a‾在下一小节中有讲解\overline{a}在下一小节中有讲解a在下一小节中有讲解

最小非负完全剩余类：
在剩余类中挑选出小于m的的所有数构成的集合

2、简化剩余系、欧拉定理与费马小定理

既约剩余类 / 简化剩余类：
∀a∈Z,a‾={n∈Z∣n≡a mod m}\forall a\in Z,\overline a=\{n\in Z|n\equiv a\ mod\ m\}∀a∈Z,a={n∈Z∣n≡a mod m}

既约剩余系 / 简化剩余系：
设m为一个正整数，在模m的所有不同简化剩余系中，从每个剩余类中任取一个数组成的整数集合，叫做模m的一个既约（简化）剩余系设m为一个正整数，在模m的所有不同简化剩余系中，从每个剩余类中任取一个数组成的整数集合，叫做模m的一个既约（简化）剩余系设m为一个正整数，在模m的所有不同简化剩余系中，从每个剩余类中任取一个数组成的整数集合，叫做模m的一个既约（简化）剩余系
Zm∗={a‾∈Z∣(a,m)=1}Z_m^*=\{\overline a\in Z|(a,m) = 1\}Zm∗​={a∈Z∣(a,m)=1}
即在最小非负完全剩余类中抽取与m互质的元素构成的集合
∣Zm∗∣=ϕ(m)|Z_m^*| = \phi(m)∣Zm∗​∣=ϕ(m)

定理1：
设m是正整数，整数a满足(a,m)=1(a,m) = 1(a,m)=1。若x遍历模m的一个简化剩余系，则ax也遍历模m的一个简化剩余系

关于欧拉函数ϕ§\phi§ϕ§：
若p为素数，则ϕ§=p−1\phi§=p-1ϕ§=p−1
若p为素数，且整数α≥1\alpha \ge 1α≥1，则ϕ(pα)=pα−pα−1=pα(1−1p)\phi(p^{\alpha})=p{\alpha}-p^{\alpha -1}=p^{\alpha}(1-\frac{1}{p})ϕ(pα)=pα−pα−1=pα(1−p1​)
若p、q为素数，则ϕ(pq)=ϕ§ϕ(q)\phi(pq) = \phi§ \phi(q)ϕ(pq)=ϕ§ϕ(q)
对于正整数nϕ(n)=nΠp∣n(1−1p)\phi(n)=n\Pi_{p|n}(1-\frac{1}{p})ϕ(n)=nΠp∣n​(1−p1​)

欧拉定理：
设m是大于1的整数，如果a是满足(a,m)=1(a,m) =1(a,m)=1的整数，则aϕ(m)≡1 mod ma^{\phi (m)}\equiv 1\ mod\ maϕ(m)≡1 mod m
利用既约剩余系和定理1即可证明
可以用来求a的逆元，最后再取一下模就可以了

费马小定理（欧拉定理的推论）：
设p是一个素数，则对于任意整数a，均有ap≡a mod pa^p\equiv a\ mod\ pap≡a mod p
证明：考虑p和a是否是整除关系，分两类讨论；若是，则模运算结果总是0；若不是，则利用欧拉定理得ap−1≡1 mod pa^{p-1}\equiv 1\ mod\ pap−1≡1 mod p，再同时乘a证毕
可以用来求a的逆元，最后再取一下模就可以了

威尔森定理：
设p是一个素数，则(p−1)!≡−1 mod p(p-1)!\equiv -1\ mod\ p(p−1)!≡−1 mod p

三、同余式

1、一次同余式

设m是一个正整数，f(x)为多项式且，f(x)=anxn+…+a1x+a0 mod m为同余式设m是一个正整数，f(x)为多项式且，f(x)=a_nx^n+…+a_1x+a_0\ mod\ m为同余式设m是一个正整数，f(x)为多项式且，f(x)=an​xn+…+a1​x+a0​ mod m为同余式
若xn不同余0模m，则n叫做f(x)的次数，an为f(x)的首项系数若x^n不同余0模m，则n叫做f(x)的次数，a_n为f(x)的首项系数若xn不同余0模m，则n叫做f(x)的次数，an​为f(x)的首项系数

若整数a满足f(a)≡0 mod m，那么x≡a mod m叫做满足该同余式的解若整数a满足f(a)\equiv 0\ mod\ m，那么x\equiv a\ mod\ m叫做满足该同余式的解若整数a满足f(a)≡0 mod m，那么x≡a mod m叫做满足该同余式的解

事实上，满足x≡a mod m的所有整数都能够使得该式成立，因此该一个剩余类叫做一个解事实上，满足x\equiv a\ mod\ m的所有整数都能够使得该式成立，因此该一个剩余类叫做一个解事实上，满足x≡a mod m的所有整数都能够使得该式成立，因此该一个剩余类叫做一个解

一次同余方程ax≡b mod max\equiv b\ mod\ max≡b mod m求解：
一次同余方程有解的充要条件是（a,m）∣b（a,m）|b（a,m）∣b，且解的个数为(a,m)(a,m)(a,m)个，证明如下：

解法如下：

这里在求逆元的时候不建议用费马小定理，因为求出来的可能不是最小的解（如果p恰好是素数，当然更加便于计算，但是最后记得要取模）

2、中国剩余定理CRT

定理证明：

唯一性证明：

3、RSA加密

四、二次同余式和平方剩余

1、二次同余式和平方剩余

设m为正整数，若同余式x2≡a mod m,(a,m)=1有解，则称a为模m的二次剩余，否则称为二次非剩余设m为正整数，若同余式x^2\equiv a\ mod\ m,(a,m)=1有解，则称a为模m的二次剩余，否则称为二次非剩余设m为正整数，若同余式x2≡a mod m,(a,m)=1有解，则称a为模m的二次剩余，否则称为二次非剩余

设p为素数，在p的一个简化剩余系中，恰有p−12个模p的二次剩余，有p−12个模p的二次非剩余设p为素数，在p的一个简化剩余系中，恰有\frac{p-1}{2}个模p的二次剩余，有\frac{p-1}{2}个模p的二次非剩余设p为素数，在p的一个简化剩余系中，恰有2p−1​个模p的二次剩余，有2p−1​个模p的二次非剩余
证明：思想是前后两两组合，过程略

Euler判定法则（判断a是否是模p的二次剩余）
设p是奇素数，(a,p)=1，则a是模p的二次剩余的充要条件是ap−12≡1 mod p，a是模p的二次非剩余的充要条件是ap−12≡−1 mod p设p是奇素数，(a,p)=1，则a是模p的二次剩余的充要条件是a^{\frac{p-1}{2}}\equiv 1\ mod\ p，a是模p的二次非剩余的充要条件是a^{\frac{p-1}{2}}\equiv -1\ mod\ p设p是奇素数，(a,p)=1，则a是模p的二次剩余的充要条件是a2p−1​≡1 mod p，a是模p的二次非剩余的充要条件是a2p−1​≡−1 mod p
注意：只针对p是素数的情况

2、勒让德符号及其计算方法

勒让德符号定义：
设p是素数，a是整数，勒让德符号定义为：设p是素数，a是整数，勒让德符号定义为：设p是素数，a是整数，勒让德符号定义为：
若a是模p的二次剩余，那么(ap)=1若a是模p的二次剩余，那么(\frac{a}{p})=1若a是模p的二次剩余，那么(pa​)=1
若a是模p的二次非剩余，那么(ap)=−1若a是模p的二次非剩余，那么(\frac{a}{p})=-1若a是模p的二次非剩余，那么(pa​)=−1
若p∣a，那么(ap)=0若p|a，那么(\frac{a}{p})=0若p∣a，那么(pa​)=0

勒让德符号性质：
(1p)=1(\frac{1}{p})=1(p1​)=1
(a+pp)=(ap)(\frac{a+p}{p})=(\frac{a}{p})(pa+p​)=(pa​)
(abp)=(ap)(bp)(\frac{ab}{p})=(\frac{a}{p})(\frac{b}{p})(pab​)=(pa​)(pb​)
当p≡1 mod 4，(−1p)=1；当p≡3 mod 4，(−1p)=−1当p\equiv1\ mod\ 4，(\frac{-1}{p})=1；当p\equiv3\ mod\ 4，(\frac{-1}{p})=-1当p≡1 mod 4，(p−1​)=1；当p≡3 mod 4，(p−1​)=−1
当p≡1、7 mod 8，(2p)=1；当p≡3、5 mod 8，(2p)=−1当p\equiv1、7\ mod\ 8，(\frac{2}{p})=1；当p\equiv3、5\ mod\ 8，(\frac{2}{p})=-1当p≡1、7 mod 8，(p2​)=1；当p≡3、5 mod 8，(p2​)=−1

Euler判定法则（用勒让德表示，判断a是否是模p的二次剩余）
设p是素奇数，则对任意整数a，有(ap)=ap−12 mod p设p是素奇数，则对任意整数a，有(\frac{a}{p})=a^{\frac{p-1}{2}}\ mod\ p设p是素奇数，则对任意整数a，有(pa​)=a2p−1​ mod p
设p是素奇数，则((2p)=(−1)p2−18设p是素奇数，则((\frac{2}{p})=(-1)^{\frac{p2-1}{8}}设p是素奇数，则((p2​)=(−1)8p2−1​

二次互反律
设p,q是互素的奇素数，则(pq)=(−1)p−12q−12(qp)设p,q是互素的奇素数，则(\frac{p}{q})=(-1)^{\frac{p-1}{2}\frac{q-1}{2}}(\frac{q}{p})设p,q是互素的奇素数，则(qp​)=(−1)2p−1​2q−1​(pq​)

五、原根和指数

1、原根和阶的概念

设m>1是整数，a是正整数，(a,m)=1，则使得ax≡1 mod m成立的最小正整数x叫做a模m的阶，记作ordm(a)设m>1是整数，a是正整数，(a,m)=1，则使得a^x\equiv 1\ mod\ m成立的最小正整数x叫做a模m的阶，记作ord_m(a)设m>1是整数，a是正整数，(a,m)=1，则使得ax≡1 mod m成立的最小正整数x叫做a模m的阶，记作ordm​(a)
其中，根据欧拉定理可知，其解是一定存在的，最大为ϕ(m)\phi(m)ϕ(m)

如果ordm(a)=ϕ(m)，则a叫做m的如果ord_m(a)=\phi(m)，则a叫做m的如果ordm​(a)=ϕ(m)，则a叫做m的原根
其中，一个质数一定存在原根，且原根的个数为ϕ(ϕ§)\phi(\phi§)ϕ(ϕ§)
除质数外，其他数不一定存在原根，例如8没有原根

性质：
①a≡b mod m，则ordm(a)=ordm(b)①a\equiv b\ mod\ m，则ord_m(a)=ord_m(b)①a≡b mod m，则ordm​(a)=ordm​(b)
②ak≡at mod m，则k≡t mod a②a^k\equiv a^t\ mod\ m，则k\equiv t\ mod\ a②ak≡at mod m，则k≡t mod a
③ordm(a)=ordm(a−1)③ord_m(a)=ord_m(a^{-1})③ordm​(a)=ordm​(a−1)

定理1：
设m>1是整数，a是正整数，(a,m)=1，则整数d使得ad≡1 mod m成立的充要条件是ordm(a)∣d设m>1是整数，a是正整数，(a,m)=1，则整数d使得a^d\equiv 1\ mod\ m成立的充要条件是ord_m(a)|d设m>1是整数，a是正整数，(a,m)=1，则整数d使得ad≡1 mod m成立的充要条件是ordm​(a)∣d

设m>1是整数，a是正整数，(a,m)=1，则ordm(a)∣ϕ(m)设m>1是整数，a是正整数，(a,m)=1，则ord_m(a)|\phi(m)设m>1是整数，a是正整数，(a,m)=1，则ordm​(a)∣ϕ(m)
（求原根的方法之一）
阶一定是ϕ(m)的因子或者它本身！！！所以在求原根时，可以通过试这些因子，来看是否阶只等于ϕ(m)来判断是否是原根阶一定是\phi(m)的因子或者它本身！！！所以在求原根时，可以通过试这些因子，来看是否阶只等于\phi(m)来判断是否是原根阶一定是ϕ(m)的因子或者它本身！！！所以在求原根时，可以通过试这些因子，来看是否阶只等于ϕ(m)来判断是否是原根

2、原根与阶的计算

定理1：
设m>1，ϕ(m)的所有不同素因子是q1…qk，则g是模m的一个原根的充要条件是gϕ(m)qi不同模于1 mod m设m>1，\phi(m)的所有不同素因子是q_1…q_k，则g是模m的一个原根的充要条件是g^{\frac{\phi(m)}{q_i}}不同模于1\ mod\ m设m>1，ϕ(m)的所有不同素因子是q1​…qk​，则g是模m的一个原根的充要条件是gqi​ϕ(m)​不同模于1 mod m

定理2：
设m>1的整数，a为整数且(a,m)=1，d≥0为整数，则ordm(ad)=ordm(a)(ordm(a),d)设m>1的整数，a为整数且(a,m)=1，d\ge 0为整数，则ord_m(a^d)=\frac{ord_m(a)}{(ord_m(a),d)}设m>1的整数，a为整数且(a,m)=1，d≥0为整数，则ordm​(ad)=(ordm​(a),d)ordm​(a)​

六、群

1、群的简介

代数系统（封闭性）——>半群（结合律）——>独异点（有单位元）——>群（有逆元）——>阿贝尔群（满足交换律）

单位元、逆元一定唯一

例子：
<Z,+>是群<Z,+>是群<Z,+>是群
<Z,×>不是群<Z,×>不是群<Z,×>不是群
<Q,×>不是，0无逆元<Q,×>不是，0无逆元<Q,×>不是，0无逆元
<Q∗,×>（除去0）是群<Q^*,×>（除去0）是群<Q∗,×>（除去0）是群
<R,+>是群<R,+>是群<R,+>是群
<R,×>不是群<R,×>不是群<R,×>不是群

例子：
<Zm,+mod>：是群，a的逆元为−a mod m，单位元为0ˉ<Z_m,+_{mod}>：是群，a的逆元为-a\ mod\ m，单位元为\bar0<Zm​,+mod​>：是群，a的逆元为−a mod m，单位元为0ˉ
<Zm,×mod>：不是群，因为逆元不一定存在<Z_m,×_{mod}>：不是群，因为逆元不一定存在<Zm​,×mod​>：不是群，因为逆元不一定存在
<Zm∗,×mod>：是群，单位元为1ˉ（就是既约剩余系）<Z_m^*,×_{mod}>：是群，单位元为\bar 1（就是既约剩余系）<Zm∗​,×mod​>：是群，单位元为1ˉ（就是既约剩余系）

定理1：
若an=e，则ordm(a)∣n若a^n=e，则ord_m(a)|n若an=e，则ordm​(a)∣n

定理2：
∀a∈G，∣a∣=∣a−1∣\forall a\in G，|a|=|a^{-1}|∀a∈G，∣a∣=∣a−1∣

定理3：
∀a∈G，∣ad∣=∣a∣(d,∣a∣)\forall a\in G，|a^d|=\frac{|a|}{(d,|a|)}∀a∈G，∣ad∣=(d,∣a∣)∣a∣​

2、子集、陪集、拉格朗日定理

子集：
设H是群G的一个非空子集，若对于非空群G的运算，H成为一个群，则H叫做群G的子群，记作H<G设H是群G的一个非空子集，若对于非空群G的运算，H成为一个群，则H叫做群G的子群，记作H<G设H是群G的一个非空子集，若对于非空群G的运算，H成为一个群，则H叫做群G的子群，记作H<G
{e}、G为G的平凡子群\{e\}、G为G的平凡子群{e}、G为G的平凡子群

子群的判定定理：
设群H是群G的一个非空子集，则H是G的非空子群的充要条件是∀a,b∈G,ab−1∈H设群H是群G的一个非空子集，则H是G的非空子群的充要条件是\forall a,b\in G,ab^{-1}\in H设群H是群G的一个非空子集，则H是G的非空子群的充要条件是∀a,b∈G,ab−1∈H

陪集：
设H为G的子集，∀a∈G，则称aH={ax∣x∈H}为G的左陪集，同理Ha为右陪集设H为G的子集，\forall a\in G，则称aH=\{ax|x\in H\}为G的左陪集，同理Ha为右陪集设H为G的子集，∀a∈G，则称aH={ax∣x∈H}为G的左陪集，同理Ha为右陪集

定理：
①a∈aH（单位元）①a\in aH（单位元）①a∈aH（单位元）
②aH=H  ⟺  a∈H（①  ⟹  ②）②aH=H\iff a\in H（①\implies ②）②aH=H⟺a∈H（①⟹②）
③aH⊂G  ⟺  a∈H（②  ⟹  ③）③aH\subset G\iff a\in H（②\implies ③）③aH⊂G⟺a∈H（②⟹③）
④aH=bH  ⟺  a−1b∈H（②  ⟹  ④）④aH=bH\iff a^{-1}b\in H（②\implies ④）④aH=bH⟺a−1b∈H（②⟹④）
⑤aH=bH/aH∩bH=∅（两个陪集的关系有且仅有两种）⑤aH=bH/aH\cap bH=\varnothing（两个陪集的关系有且仅有两种）⑤aH=bH/aH∩bH=∅（两个陪集的关系有且仅有两种）
⑥∣aH∣=∣bH∣⑥|aH|=|bH|⑥∣aH∣=∣bH∣
⑦G=∪Ha（所有陪集的并集）⑦G=\cup Ha（所有陪集的并集）⑦G=∪Ha（所有陪集的并集）

拉格朗日定理：
设∣G∣=N，∣H∣=n，[G:H]=j。因为[G:H]=j，即群G关于子群H的右陪集的个数是j。设|G|=N，|H|=n，[G:H]=j。因为[G:H]=j，即群G关于子群H的右陪集的个数是j。设∣G∣=N，∣H∣=n，[G:H]=j。因为[G:H]=j，即群G关于子群H的右陪集的个数是j。
G=Ha1∪Ha2∪…∪Haj，则有∣Ha1∣=∣Ha2∣=…∣Haj∣=nG=Ha_1\cup Ha_2\cup …\cup Ha_j，则有|Ha_1|=|Ha_2|=…|Ha_j|=nG=Ha1​∪Ha2​∪…∪Haj​，则有∣Ha1​∣=∣Ha2​∣=…∣Haj​∣=n

3、正规子群、商群、同态

正规子群：
设G是群，H<G，若对于G中任何元素a，均有aH=Ha，则H为G的正规子群，记为H⊲G设G是群，H<G，若对于G中任何元素a，均有aH=Ha，则H为G的正规子群，记为H\lhd G设G是群，H<G，若对于G中任何元素a，均有aH=Ha，则H为G的正规子群，记为H⊲G
{e}、G是平凡正规子群\{e\}、G是平凡正规子群{e}、G是平凡正规子群
G为Abel群时，其任何子群均为正规子群G为Abel群时，其任何子群均为正规子群G为Abel群时，其任何子群均为正规子群

H是G的正规子群，等价于：（互推）H是G的正规子群，等价于：（互推）H是G的正规子群，等价于：（互推）
①∀a∈G,h∈H,aha−1∈H①\forall a\in G,h\in H,aha^{-1}\in H①∀a∈G,h∈H,aha−1∈H
②∀a∈G,aHa−1⊂H②\forall a\in G,aHa^{-1}\subset H②∀a∈G,aHa−1⊂H
③∀a∈G,aHa−1=H③\forall a\in G,aHa^{-1}=H③∀a∈G,aHa−1=H
①  ⟹  前提  ⟹  ③  ⟹  ②  ⟹  ①①\implies 前提\implies ③\implies ②\implies ①①⟹前提⟹③⟹②⟹①

商群：
设H⊲G，令G/H={aH∣a∈G}代表正规子群H在群G中的全部不同的陪集组成的集合，在G/H上定义运算∗：(aH)∗(bH)=(ab)H，则G/H在该运算下构成一个群设H\lhd G，令G/H=\{aH|a\in G\}代表正规子群H在群G中的全部不同的陪集组成的集合，在G/H上定义运算*：(aH)*(bH)=(ab)H，则G/H在该运算下构成一个群设H⊲G，令G/H={aH∣a∈G}代表正规子群H在群G中的全部不同的陪集组成的集合，在G/H上定义运算∗：(aH)∗(bH)=(ab)H，则G/H在该运算下构成一个群
该群的单位元为H，(aH)−1=a−1H该群的单位元为H，(aH)^{-1}=a{-1}H该群的单位元为H，(aH)−1=a−1H
G/H就是G关于H的商群G/H就是G关于H的商群G/H就是G关于H的商群

同态：
G和G′是两个群，f是G到G′的映射，如果对任意的a,b∈G，都有f(ab)=f(a)f(b)，则f为同态G和G’是两个群，f是G到G’的映射，如果对任意的a,b\in G，都有f(ab)=f(a)f(b)，则f为同态G和G′是两个群，f是G到G′的映射，如果对任意的a,b∈G，都有f(ab)=f(a)f(b)，则f为同态

自然同态：
G与G/H同态

f=ϕθf=\phi \thetaf=ϕθ
f:G→G′;ϕ:G/N→G′;θ:G→G/N，也就是从后往前看f:G\to G’;\phi:G/N\to G’;\theta :G\to G/N，也就是从后往前看f:G→G′;ϕ:G/N→G′;θ:G→G/N，也就是从后往前看

4、循环群

若∣G∣=∞，则G=={e,a,a2,…,an,…}若|G|=\infty ，则G==\{e,a,a^2,…,an,…\}若∣G∣=∞，则G=<a>={e,a,a2,…,an,…}
若∣G∣=n<∞,则G=={e,a,a2,…,an}若|G|=n<\infty,则G==\{e,a,a^2,…,an\}若∣G∣=n<∞,则G=<a>={e,a,a2,…,an}

设p为素数，则Zp∗为循环群，如Z5∗={1,2,3,4}=<2>=<3>设p为素数，则Z_p^{*为循环群，如Z_5}*=\{1,2,3,4\}=<2>=<3>设p为素数，则Zp∗​为循环群，如Z5∗​={1,2,3,4}=<2>=<3>

同构的意义下，循环群仅有两个：
<Z,+>无限群同构，且=<1>=<−1><Z,+>无限群同构，且=<1>=<-1><Z,+>无限群同构，且=<1>=<−1>
<Z,+mod>有限群同构，且=<1ˉ><Z,+_{mod}>有限群同构，且=<\bar 1><Z,+mod​>有限群同构，且=<1ˉ>

5、置换群

置换群：
设X为非空集合，定义在X上的所有可逆映射，关于映射的复合运算所构成的一个群，称为定义在X上的对称群，即为Sx设X为非空集合，定义在X上的所有可逆映射，关于映射的复合运算所构成的一个群，称为定义在X上的对称群，即为S_x设X为非空集合，定义在X上的所有可逆映射，关于映射的复合运算所构成的一个群，称为定义在X上的对称群，即为Sx​
Sx的任一子群，称为变换群。特别地，当X为有限集时，记∣X∣=n，则记Sx为Sn（n次对称群），此时称变换群为置换群S_x的任一子群，称为变换群。特别地，当X为有限集时，记|X|=n，则记S_x为S_n（n次对称群），此时称变换群为置换群Sx​的任一子群，称为变换群。特别地，当X为有限集时，记∣X∣=n，则记Sx​为Sn​（n次对称群），此时称变换群为置换群
总的来说，置换群就是有限集的对称群的子群总的来说，置换群就是有限集的对称群的子群总的来说，置换群就是有限集的对称群的子群

置换群不是Abel群，不满足交换律置换群不是Abel群，不满足交换律置换群不是Abel群，不满足交换律

∣Sn∣=n!|S_n|=n!∣Sn​∣=n!

设σ∈Sn，若σ满足σ(i1)=i2,σ(i2)=i3,…,σ(ik−1)=ik（因为双射使之成立），其中1≤k≤n，且保持其他元素不变，这称置换σ为k−轮换，记作σ=(i1i2…ik)设\sigma \in S_n，若\sigma 满足\sigma(i_1)=i_2,\sigma(i_2)=i_3,…,\sigma(i_{k-1})=i_k（因为双射使之成立），其中1\le k\le n，且保持其他元素不变，这称置换\sigma为k-轮换，记作\sigma =(i_1i_2…i_k)设σ∈Sn​，若σ满足σ(i1​)=i2​,σ(i2​)=i3​,…,σ(ik−1​)=ik​（因为双射使之成立），其中1≤k≤n，且保持其他元素不变，这称置换σ为k−轮换，记作σ=(i1​i2​…ik​)
当k=2时，置换(i1i2)称为对换当k=2时，置换(i_1i_2)称为对换当k=2时，置换(i1​i2​)称为对换
1−轮换即为恒等置换I，即(1)=(2)=…=(n)1-轮换即为恒等置换I，即(1)=(2)=…=(n)1−轮换即为恒等置换I，即(1)=(2)=…=(n)

两个循环置换中如果不存在相同的元素，则称这两个循环置换互不相交，例如两个循环置换中如果不存在相同的元素，则称这两个循环置换互不相交，例如两个循环置换中如果不存在相同的元素，则称这两个循环置换互不相交，例如
(123456652134)=(1 6 4)(2 5 3) \begin{pmatrix} 1 & 2 & 3 & 4 & 5 & 6\\ 6 & 5 & 2 & 1 & 3 & 4\\ \end{pmatrix} =(1\ 6\ 4)(2\ 5\ 3)(16​25​32​41​53​64​)=(1 6 4)(2 5 3)

任意一个置换都可以表示成一些不相交循环置换的乘积，如上

任意置换都可以分解成若干对换的乘积
σ=(i1i2…ik)=(i1i2)(i2i3)…(ik−1ik)\sigma =(i_1i_2…i_k)=(i_1i_2)(i_2i_3)…(i_{k-1}i_k)σ=(i1​i2​…ik​)=(i1​i2​)(i2​i3​)…(ik−1​ik​)

七、环与域

1、环

定义——环：
设R非空，在R上引入两个运算+∗，若<R,+>构成Abel群，<R,∗>满足封闭性、结合律，且∗对于+的分配律成立，即∀a,b,c∈R,a∗(b+c)=a∗b+a∗c,(b+c)∗a=b∗a+c∗a，则<R,+,∗>为环设R非空，在R上引入两个运算+*，若<R,+>构成Abel群，<R,*>满足封闭性、结合律，且*对于+的分配律成立，即\forall a,b,c\in R,a*(b+c)=a*b+a*c,(b+c)*a=b*a+c*a，则<R,+,*>为环设R非空，在R上引入两个运算+∗，若<R,+>构成Abel群，<R,∗>满足封闭性、结合律，且∗对于+的分配律成立，即∀a,b,c∈R,a∗(b+c)=a∗b+a∗c,(b+c)∗a=b∗a+c∗a，则<R,+,∗>为环

定义——交换环：
若环R中，∗满足构成交换半群，则R称为交换环若环R中，*满足构成交换半群，则R称为交换环若环R中，∗满足构成交换半群，则R称为交换环

定义——零元、单位元：
对于第一个运算而言：称其单位元为零元（一定存在）对于第一个运算而言：称其单位元为零元（一定存在）对于第一个运算而言：称其单位元为零元（一定存在）
对于第二个运算而言：若环R中∃e,使得∀a∈R，满足e∗a=a∗e=a，则称e为单位元（由定义可见，单位元不一定存在）对于第二个运算而言：若环R中\exist e,使得\forall a\in R，满足e*a=a*e=a，则称e为单位元（由定义可见，单位元不一定存在）对于第二个运算而言：若环R中∃e,使得∀a∈R，满足e∗a=a∗e=a，则称e为单位元（由定义可见，单位元不一定存在）

定义——负元、可逆元：
对于第一个运算而言：称其逆元为负元（一定存在）对于第一个运算而言：称其逆元为负元（一定存在）对于第一个运算而言：称其逆元为负元（一定存在）
对于第二个运算而言：∀a∈R，若∃b∈R，使得a∗b=b∗a=e，则称a可逆，a为可逆元，b为a的逆元，可逆元也称为环R的对于第二个运算而言：\forall a\in R，若\exist b\in R，使得a*b=b*a=e，则称a可逆，a为可逆元，b为a的逆元，可逆元也称为环R的对于第二个运算而言：∀a∈R，若∃b∈R，使得a∗b=b∗a=e，则称a可逆，a为可逆元，b为a的逆元，可逆元也称为环R的单位，所有单位构成的群称为R的，所有单位构成的群称为R的，所有单位构成的群称为R的单位群，记作U®，记作U®，记作U®

例子：
<Z,+,∗>：零元：0，单位元：1，U(Z)={1,−1}<Z,+,*>：零元：0，单位元：1，U(Z)=\{1,-1\}<Z,+,∗>：零元：0，单位元：1，U(Z)={1,−1}
<Zm,+,∗>：零元：0ˉ，单位元：1ˉ，U(Z)=Zm∗<Z_m,+,*>：零元：\bar 0，单位元：\bar 1，U(Z)=Z_m^*<Zm​,+,∗>：零元：0ˉ，单位元：1ˉ，U(Z)=Zm∗​

定义——有零因子环：
设R=<S,+,∗>为一个环，若∃a,b∈S，满足a,b≠0,a∗b=0，则称R为有零因子环，否则为无零因子环，a为左零因子，b为右零因子，若一个元素是左、右零因子，则该元素为零因子。环内不是左、右零因子的元素为正则元设R=<S,+,*>为一个环，若\exist a,b\in S，满足a,b\neq 0,a*b=0，则称R为有零因子环，否则为无零因子环，a为左零因子，b为右零因子，若一个元素是左、右零因子，则该元素为零因子。环内不是左、右零因子的元素为正则元设R=<S,+,∗>为一个环，若∃a,b∈S，满足a,b=0,a∗b=0，则称R为有零因子环，否则为无零因子环，a为左零因子，b为右零因子，若一个元素是左、右零因子，则该元素为零因子。环内不是左、右零因子的元素为正则元
无零因子环中，消去律成立，即∀a,b,c∈S,a∗c=b∗c，且c≠0，则a=b（值得注意的是，群中的消去律成立的原因是逆元存在，而环中消去律成立的原因是无零因子）无零因子环中，消去律成立，即\forall a,b,c\in S,a*c=b*c，且c\neq 0，则a=b（值得注意的是，群中的消去律成立的原因是逆元存在，而环中消去律成立的原因是无零因子）无零因子环中，消去律成立，即∀a,b,c∈S,a∗c=b∗c，且c=0，则a=b（值得注意的是，群中的消去律成立的原因是逆元存在，而环中消去律成立的原因是无零因子）

定义——子环：
设R为环，S为非空子集，若S关于R的代数运算，亦构成环，则称S为R的子环，记作S<R，若3Z<Z，Z<Q，Z3不是Z的子环（运算不同）设R为环，S为非空子集，若S关于R的代数运算，亦构成环，则称S为R的子环，记作S\lt R，若3Z\lt Z，Z\lt Q，Z_3不是Z的子环（运算不同）设R为环，S为非空子集，若S关于R的代数运算，亦构成环，则称S为R的子环，记作S<R，若3Z<Z，Z<Q，Z3​不是Z的子环（运算不同）

判定子环定理：
设R为环，S为R的非空子集，则S<R  ⟺  ∀a,b∈R下，∀a,b∈S，且a−b∈S，a∗b∈S设R为环，S为R的非空子集，则S\lt R \iff \forall a,b\in R下，\forall a,b \in S，且a-b\in S，a*b\in S设R为环，S为R的非空子集，则S<R⟺∀a,b∈R下，∀a,b∈S，且a−b∈S，a∗b∈S
证明：使用了最基本的子群判定定理，即a∗b−1∈S，第一个运算要满足交换群，第二个运算要满足封闭性，结合律不需要考虑，因为元素本身即满足结合律证明：使用了最基本的子群判定定理，即a*b^{-1}\in S，第一个运算要满足交换群，第二个运算要满足封闭性，结合律不需要考虑，因为元素本身即满足结合律证明：使用了最基本的子群判定定理，即a∗b−1∈S，第一个运算要满足交换群，第二个运算要满足封闭性，结合律不需要考虑，因为元素本身即满足结合律

定义——整环
有单位元的无零因子的交换环为整环有单位元的无零因子的交换环为整环有单位元的无零因子的交换环为整环
其中，Z[i]={a+bi∣a,b∈Z}为高斯整环其中，Z[i]=\{a+bi|a,b\in Z\}为高斯整环其中，Z[i]={a+bi∣a,b∈Z}为高斯整环

定义——除环：
环R中每一个非零元都存在逆元，那么该环为除环环R中每一个非零元都存在逆元，那么该环为除环环R中每一个非零元都存在逆元，那么该环为除环

定义——域：
可交换的除环即为域，记作F可交换的除环即为域，记作F可交换的除环即为域，记作F
即环满足交换律，且所有非零元有逆元即环满足交换律，且所有非零元有逆元即环满足交换律，且所有非零元有逆元
其中，对于素数p，<Zp,+mod,∗mod>=Fp为最基本的有限域其中，对于素数p，<Z_p,+_{mod},*_{mod}>=F_p为最基本的有限域其中，对于素数p，<Zp​,+mod​,∗mod​>=Fp​为最基本的有限域

域的性质：
域一定是整环域一定是整环域一定是整环
整环不一定是域整环不一定是域整环不一定是域
有限整环一定是域有限整环一定是域有限整环一定是域

2、环同态、环同构

设R,R′是两个环，如果f满足对∀a,b∈R，都有f(a+b)=f(a)+f(b)，且f(ab)=f(a)f(b)，则称映射f:R→R′为环同态设R,R’是两个环，如果f满足对\forall a,b\in R，都有f(a+b)=f(a)+f(b)，且f(ab)=f(a)f(b)，则称映射f:R\to R’为环同态设R,R′是两个环，如果f满足对∀a,b∈R，都有f(a+b)=f(a)+f(b)，且f(ab)=f(a)f(b)，则称映射f:R→R′为环同态
如果f是一对一的，那么f是同构如果f是一对一的，那么f是同构如果f是一对一的，那么f是同构
值得注意的是，等号前面的+和等号后面的+是不同的，分别是R和R’的第一个运算

例子：
Z→Zm:f:n→nˉZ\to Z_m:f:n\to \bar nZ→Zm​:f:n→nˉ
这个例子的意义是成功将这个例子的意义是成功将这个例子的意义是成功将无限环映射到有限环

定义：
设R为一个环，如果存在一个最小正整数n使得∀a∈R，都有na=0，则称环R的特征为n，记作char®=n，如果不存特征，那么char®=0设R为一个环，如果存在一个最小正整数n使得\forall a\in R，都有na=0，则称环R的特征为n，记作char®=n，如果不存特征，那么char®=0设R为一个环，如果存在一个最小正整数n使得∀a∈R，都有na=0，则称环R的特征为n，记作char®=n，如果不存特征，那么char®=0
char(Zm)=mchar(Z_m)=mchar(Zm​)=m

性质：
整环R，char®=0/char®=p整环R，char®=0/char®=p整环R，char®=0/char®=p
有限域的特征必为素数\ 有限域的特征必为素数 有限域的特征必为素数
若R为可交换环，且char®=p，则∀a,b∈R，(a+b)p=ap+bp若R为可交换环，且char®=p，则\forall a,b\in R，(a+b)^p=ap+b^p若R为可交换环，且char®=p，则∀a,b∈R，(a+b)p=ap+bp

3、子环、理想

定义——理想：
设R为环，I为非空子集，∀r1,r2∈I，有r1−r2∈I，且∀r∈I，∀a∈R，有ar，ra∈I，则I为R的理想，记作I⊲R设R为环，I为非空子集，\forall r_1,r_2\in I，有r_1-r_2\in I，且\forall r\in I，\forall a\in R，有ar，ra\in I，则I为R的理想，记作I\lhd R设R为环，I为非空子集，∀r1​,r2​∈I，有r1​−r2​∈I，且∀r∈I，∀a∈R，有ar，ra∈I，则I为R的理想，记作I⊲R
{0}记为零理想，R记为单位理想，二者统称为平凡理想\{0\}记为零理想，R记为单位理想，二者统称为平凡理想{0}记为零理想，R记为单位理想，二者统称为平凡理想

定义——单环：
有且仅有平凡理想的非零环记为单环，除环必为单环有且仅有平凡理想的非零环记为单环，除环必为单环有且仅有平凡理想的非零环记为单环，除环必为单环

设R是一个环，T是R的一非空子集，则将R中所有包含T的理想的交集记为由T生成的理想，记作。特别地，当T={a}时，将记为并记为由a生成的主理想设R是一个环，T是R的一非空子集，则将R中所有包含T的理想的交集记为由T生成的理想，记作。特别地，当T=\{a\}时，将记为并记为由a生成的主理想设R是一个环，T是R的一非空子集，则将R中所有包含T的理想的交集记为由T生成的理想，记作<T>。特别地，当T={a}时，将<T>记为<a>并记为由a生成的主理想
特别地，单号给R为含单位元的交换环，={ar∣r∈R}特别地，单号给R为含单位元的交换环，=\{ar|r\in R\}特别地，单号给R为含单位元的交换环，<a>={ar∣r∈R}

性质——主理想
整数环Z中任一理想都是主理想整数环Z中任一理想都是主理想整数环Z中任一理想都是主理想
dZ=,dZ⊲ZdZ=,dZ\lhd ZdZ=<d>,dZ⊲Z

4、多项式环、多项式域

以下凡是环R的均可以换成域F

设R为含单位元的环，R[x]={f(x)=a0+a1x1+…+anxn∣ai∈R,n∈Z}构成一个环，称为多项式环，单位元是1，零元是0，不一定可逆设R为含单位元的环，R[x]=\{f(x)=a_0+a_1x_1+…+a_nx_n|a_i\in R,n\in Z\}构成一个环，称为多项式环，单位元是1，零元是0，不一定可逆设R为含单位元的环，R[x]={f(x)=a0​+a1​x1​+…+an​xn​∣ai​∈R,n∈Z}构成一个环，称为多项式环，单位元是1，零元是0，不一定可逆
注意其中的关系，R[x]本身是一个环，F[x]本身也是一个环，但是其中的系数属于环或者域

定理：
设f(x),g(x)∈F[x]且g(x)≠0，则∃q(x),r(x)，存在f(x)=q(x)g(x)+r(x)且r(x)=0或deg(r(x))<deg(g(x))设f(x),g(x)\in F[x]且g(x)\neq 0，则\exist q(x),r(x)，存在f(x)=q(x)g(x)+r(x)且r(x)=0或deg(r(x))\lt deg(g(x))设f(x),g(x)∈F[x]且g(x)=0，则∃q(x),r(x)，存在f(x)=q(x)g(x)+r(x)且r(x)=0或deg(r(x))<deg(g(x))
域上的代数运算与Z上的代数运算相同域上的代数运算与Z上的代数运算相同域上的代数运算与Z上的代数运算相同

定义——可约：
f(x)∈F[x]且f(x)非常量，若f(x)除了和其自身以外无其他因式，则f(x)是不可约的f(x)\in F[x]且f(x)非常量，若f(x)除了和其自身以外无其他因式，则f(x)是不可约的f(x)∈F[x]且f(x)非常量，若f(x)除了和其自身以外无其他因式，则f(x)是不可约的
注意：多项式是否可约与其所在的系数域有关！约后的形式也与其有关

定义——公因式：
设f(x),g(x)∈F[x]，若d(x)∣f(x)∧d(x)∣g(x)，约定d(x)首项系数为1，则d(x)∣dmax(x)，d(x)=f(x)q(x)+g(x)r(x)设f(x),g(x)\in F[x]，若d(x)|f(x)\land d(x)|g(x)，约定d(x)首项系数为1，则d(x)|d_{max}(x)，d(x)=f(x)q(x)+g(x)r(x)设f(x),g(x)∈F[x]，若d(x)∣f(x)∧d(x)∣g(x)，约定d(x)首项系数为1，则d(x)∣dmax​(x)，d(x)=f(x)q(x)+g(x)r(x)

多项式Euclid除法：
设f(x),g(x)∈R[x]，则一定存在多项式)q(x)、r(x)使得d(x)=f(x)q(x)+g(x)r(x)，deg r(x)<deg g(x)设f(x),g(x)\in R[x]，则一定存在多项式)q(x)、r(x)使得d(x)=f(x)q(x)+g(x)r(x)，deg\ r(x)\lt deg\ g(x)设f(x),g(x)∈R[x]，则一定存在多项式)q(x)、r(x)使得d(x)=f(x)q(x)+g(x)r(x)，deg r(x)<deg g(x)

定理：
设p(x)∈F[x]且p(x)不可约，则<p(x)>为极大理想，从而F[x]/<p(x)>是一个域（任意有限域都与之同构）设p(x)\in F[x]且p(x)不可约，则<p(x)>为极大理想，从而F[x]/<p(x)>是一个域（任意有限域都与之同构）设p(x)∈F[x]且p(x)不可约，则<p(x)>为极大理想，从而F[x]/<p(x)>是一个域（任意有限域都与之同构）
特别地，当F=Fp，则∣F[x]/<p(x)>∣=pn，记F[x]/<p(x)>为Fpn特别地，当F=F_p，则|F[x]/<p(x)>|=p^{n，记F[x]/<p(x)>为F_{p}n}特别地，当F=Fp​，则∣F[x]/<p(x)>∣=pn，记F[x]/<p(x)>为Fpn​

定理：
设f(x)∈F[x]，则f(x)的次数最小的因式p(x)不可约且deg(p(x))≤n2deg(f(x))设f(x)\in F[x]，则f(x)的次数最小的因式p(x)不可约且deg(p(x))\le \frac{n}{2}deg(f(x))设f(x)∈F[x]，则f(x)的次数最小的因式p(x)不可约且deg(p(x))≤2n​deg(f(x))
推论：
设f(x)∈F[x]，deg(f(x))=n，p1(x),p2(x),…,pm(x)为f(x)的所有次数≤n2的不可约多项式，若pi不能整除f(x)，那么f(x)不可约设f(x)\in F[x]，deg(f(x))=n，p_1(x),p_2(x),…,p_m(x)为f(x)的所有次数\le \frac{n}{2}的不可约多项式，若p_i不能整除f(x)，那么f(x)不可约设f(x)∈F[x]，deg(f(x))=n，p1​(x),p2​(x),…,pm​(x)为f(x)的所有次数≤2n​的不可约多项式，若pi​不能整除f(x)，那么f(x)不可约

八、椭圆曲线

1、椭圆曲线的概念

定义——椭圆曲线：
定义在Fp上的椭圆曲线，Ep(a,b)={(x,y)∣y2=x3+ax+b,4a2+27b2≠0，a,b∈Fp}∪{∂}定义在F_p上的椭圆曲线，E_p(a,b)=\{(x,y)|y^2=x3+ax+b,4a^2+27b2\neq 0，a,b\in F_p\}\cup \{\partial\}定义在Fp​上的椭圆曲线，Ep​(a,b)={(x,y)∣y2=x3+ax+b,4a2+27b2=0，a,b∈Fp​}∪{∂}

2、椭圆曲线群的构造

定义——椭圆曲线群：
在Ep(a,b)上引入代数运算+，构成Abel群在E_p(a,b)上引入代数运算+，构成Abel群在Ep​(a,b)上引入代数运算+，构成Abel群
其满足封闭性和结合律，单位元是∂，逆元就是横坐标不变，纵坐标变成相反数其满足封闭性和结合律，单位元是\partial，逆元就是横坐标不变，纵坐标变成相反数其满足封闭性和结合律，单位元是∂，逆元就是横坐标不变，纵坐标变成相反数

运算定义：

运算公式：
设P(x1,x2),Q(x2,y2),R(x3,y3)=P+Q设P(x_1,x_2),Q(x_2,y_2),R(x_3,y_3)=P+Q设P(x1​,x2​),Q(x2​,y2​),R(x3​,y3​)=P+Q
  ⟹  {x3=λ2−x1−x2y3=λ(x1−x3)−y1\implies \begin{cases} x_3=\lambda ^2-x_1-x_2\\ y_3=\lambda (x_1-x_3)-y_1 \end{cases}⟹{x3​=λ2−x1​−x2​y3​=λ(x1​−x3​)−y1​​
其中λ={y2−y1x2−x1,P=/Q3x2+a2y,P=Q其中\lambda= \begin{cases} \frac{y_2-y_1}{x_2-x_1}, & \text{P=/Q} \\[2ex] \frac{3x^2+a}{2y}, & \text{P=Q} \end{cases}其中λ=⎩⎨⎧​x2​−x1​y2​−y1​​,2y3x2+a​,​P=/QP=Q​

黑客/网络安全学习包

资料目录

1. 成长路线图&学习规划

2. 配套视频教程

3. SRC&黑客文籍

4. 护网行动资料

5. 黑客必读书单

6. 面试题合集

因篇幅有限，仅展示部分资料，需要点击下方链接即可前往获取

优快云大礼包：《黑客&网络安全入门&进阶学习资源包》免费分享

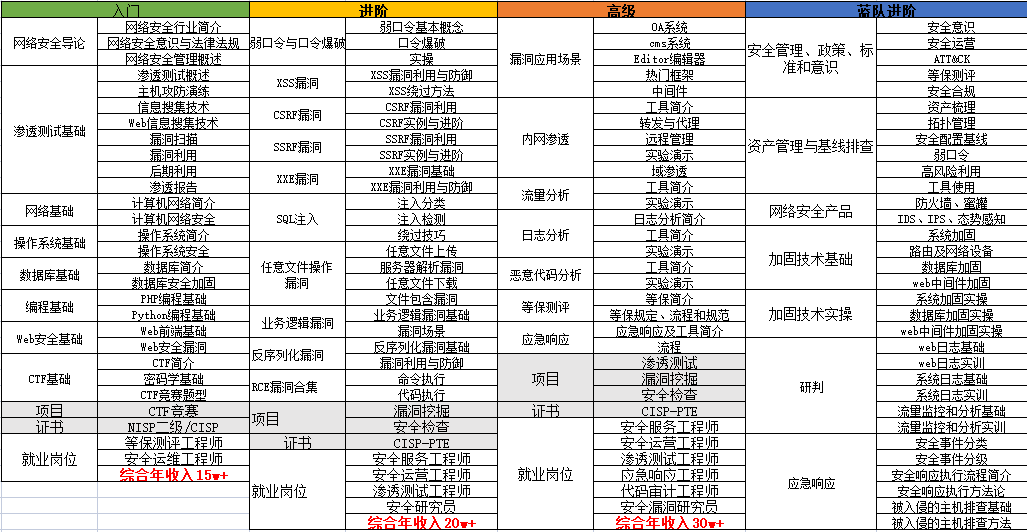
1.成长路线图&学习规划

要学习一门新的技术，作为新手一定要先学习成长路线图，方向不对，努力白费。

对于从来没有接触过网络安全的同学，我们帮你准备了详细的学习成长路线图&学习规划。可以说是最科学最系统的学习路线，大家跟着这个大的方向学习准没问题。

因篇幅有限，仅展示部分资料，需要点击下方链接即可前往获取

优快云大礼包：《黑客&网络安全入门&进阶学习资源包》免费分享

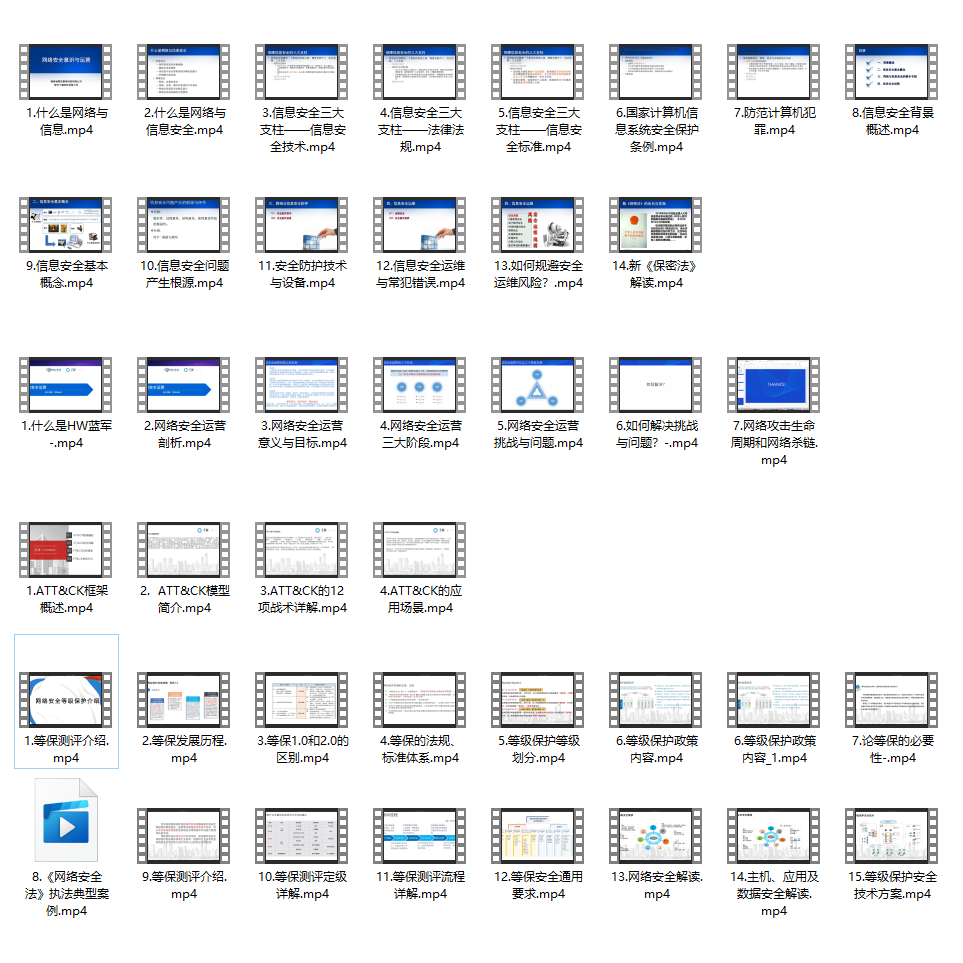
2.视频教程

很多朋友都不喜欢晦涩的文字，我也为大家准备了视频教程，其中一共有21个章节，每个章节都是当前板块的精华浓缩。

因篇幅有限，仅展示部分资料，需要点击下方链接即可前往获取

优快云大礼包：《黑客&网络安全入门&进阶学习资源包》免费分享

3.SRC&黑客文籍

大家最喜欢也是最关心的SRC技术文籍&黑客技术也有收录

SRC技术文籍：

黑客资料由于是敏感资源，这里不能直接展示哦！

4.护网行动资料

其中关于HW护网行动，也准备了对应的资料，这些内容可相当于比赛的金手指！

5.黑客必读书单

**

**

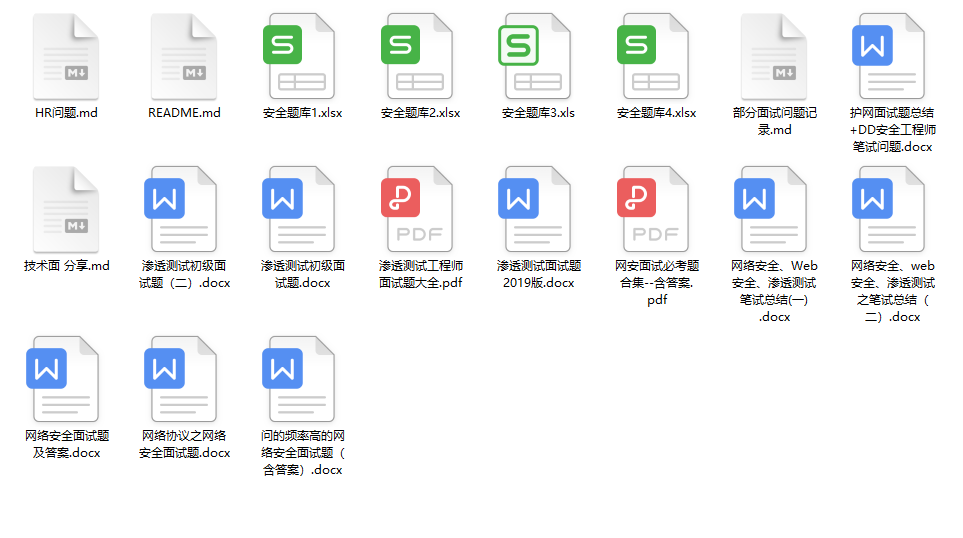
6.面试题合集

当你自学到这里，你就要开始思考找工作的事情了，而工作绕不开的就是真题和面试题。

更多内容为防止和谐，可以扫描获取~

因篇幅有限，仅展示部分资料，需要点击下方链接即可前往获取

优快云大礼包：《黑客&网络安全入门&进阶学习资源包》免费分享