目录
(一)古典密码
1.摩斯密码
2.移位密码
(1)凯撒密码
(2)栅栏密码
①常规型
②W型
(3)曲路密码
(4)列移位
(5)rot13
3.替换密码
(1)行置换密码
(2)棋盘密码
(3)vigenere维吉尼亚密码
(4)培根密码
(5)猪圈密码
(6)键盘密码
①电脑键盘
②键盘围成的密码
(7)盲文密码
(8)幂数加密/云影密码
(9)brainfuck
(10)Ook
(11)标准银河字母
(12)简单替换密码
(二)编码
1.ASCII编码
2.Base编码
3.unicode编码
4.url编码
5.html编码
(1)普通html编码
(2)html实体编码
6.rabbit编码
7.python反编译
8.quipquip词频分析
(三)现代密码学–对称加密
1.DES
2.AES
3.RC4
(四)现代密码学–非对称加密
1.RSA
(1)基础已知p、q、e求d
(2)知道加密后的文本和公钥文本(就是知道了n、p、q、e、c求m)
(3)知道加密后的文本和私钥文本
(4)RSA共模攻击
(5)分解素数多于两个
(6)n分解出来就一个(即n是质数)
2.DH
3.ECC
(1)椭圆曲线加密基础
(2)椭圆曲线数字签名
4.DSA
5.ElGamal
(五)国密
(六)用提取、删除、替换字符
(七)01或者AB这种相反面
(八)Linux系统的 shadow 文件格式
(九)MD5
(一)古典密码
1.摩斯密码
有时候一串101010可能代表的是-.-.-.

2.移位密码
(1)凯撒密码
密码统一移动几位
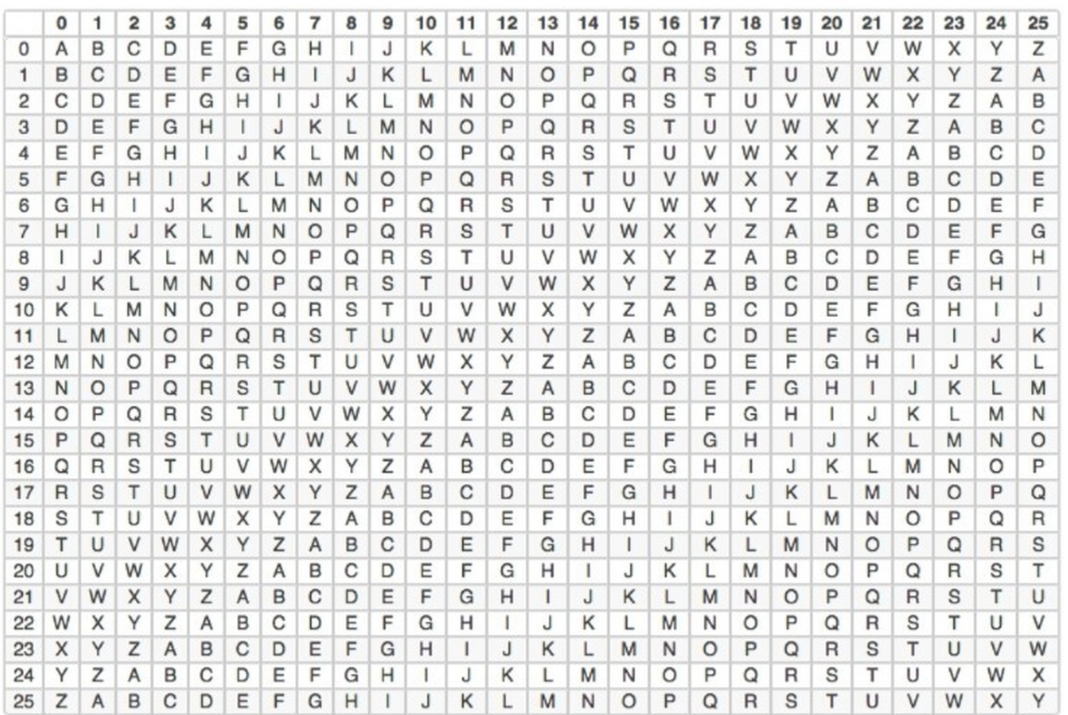
(2)栅栏密码
①常规型
栅栏密码是一种相对简单但又具有一定保密性的加密方法。它的原理是将明文按照一定的行数写成栅栏状,然后按列读取得到密文。例如,明文“HELLO WORLD”设定行数为2,写成栅栏状为:
H L O R E L W D
按列读取得到密文“HLOR ELWD
②W型
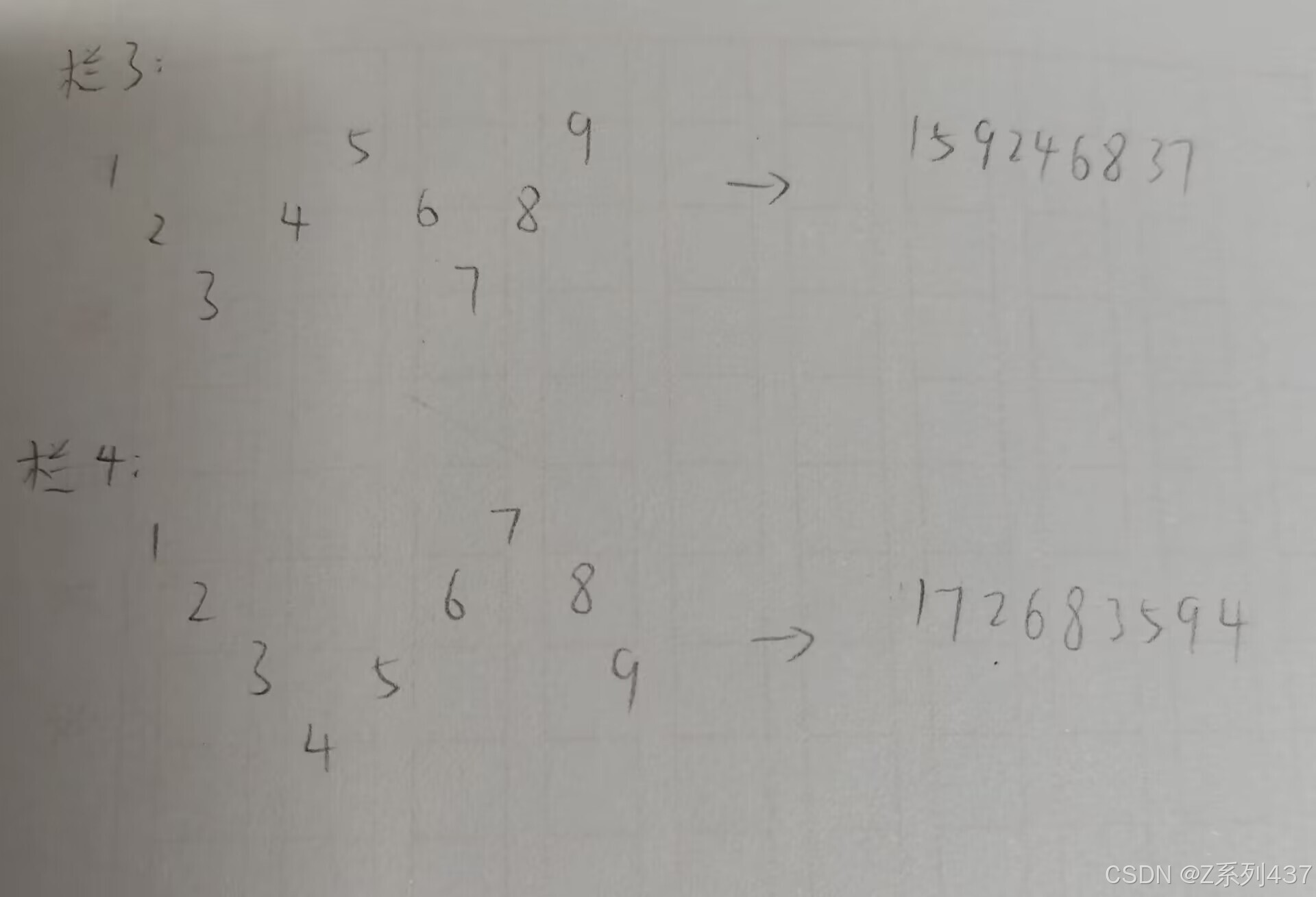
(3)曲路密码

(4)列移位
举例: 明文:The quick brown fox jumps over the lazy dog 密钥:how are u

密文:qoury inpho Tkool hbxva uwmtd cfseg erjez
(5)rot13
就是凯撒密码偏移量为13的情况
3.替换密码
(1)行置换密码
加密

解密

(2)棋盘密码

明文 HELLO,加密后就是 23 15 31 31 34
(3)vigenere维吉尼亚密码

(4)培根密码

(5)猪圈密码

(6)键盘密码
①电脑键盘

例如:11为Q,23为D
②键盘围成的密码
例如:xrv为c
(7)盲文密码

(8)幂数加密/云影密码

(9)brainfuck
++++++++++\[>+++++++>++++++++++>+++>+<<<<-\]
++.>+.+++++++…+++.>++.<<+++++++++++++++.
.+++.------.--------.>+.>.
(10)Ook
#-\*-coding:utf-8-\*-
import sys
from collections import deque
class LoopError(Exception):
pass
class OokParser(object):
def \_\_init\_\_(self):
self.BEGIN = ('!', '?')
self.END = ('?', '!')
self.primitives = {('.', '.'): 'inc',
('!', '!'): 'dec',
('.', '?'): 'right',
('?', '.'): 'left',
('!', '.'): 'write',
('.', '!'): 'read'}
def parse(self, input\_text):
items = input\_text.lower().replace('ook','').replace(' ', '').replace('\\n','').replace('\\r','')
for i in range(0, len(items), 2):
x = (items\[i\], items\[i+1\])
if x in self.primitives or x in (self.BEGIN, self.END):
yield x
class BrainfuckParser(object):
def \_\_init\_\_(self):
self.BEGIN = '\['
self.END = '\]'
self.primitives = {'+': 'inc',
'-': 'dec',
'>': 'right',
'<': 'left',
'.': 'write',
',': 'read'}
def parse(self, input\_text):
for x in input\_text:
if x in self.primitives or x in (self.BEGIN, self.END):
yield x
class Interpreter(object):
MAX\_NESTED\_LOOPS = 1000
def \_\_init\_\_(self, ook\_mode=True):
self.bf\_parser = BrainfuckParser()
self.ook\_parser = OokParser()
self.set\_parser(ook\_mode and self.ook\_parser or self.bf\_parser)
def reset(self):
self.cells = deque(\[0\])
self.index = 0
self.input\_buffer = \[\]
self.output\_buffer = \[\]
self.open\_loops = 0
self.loop = \[\]
def inc(self):
self.cells\[self.index\] += 1
def dec(self):
self.cells\[self.index\] -= 1
def right(self):
self.index += 1
if self.index >= len(self.cells):
self.cells.append(0)
def left(self):
if self.index == 0:
self.cells.appendleft(0)
else:
self.index -= 1
def write(self):
self.output\_buffer.append(self.cells\[self.index\])
def read(self):
try:
self.cells\[self.index\] = int(raw\_input("Your input: "))
except (TypeError, ValueError):
print ("Invalid input! Continuing ...")
def as\_ascii(self):
return "".join(\[chr(c) for c in self.output\_buffer\])
def set\_parser(self, parser):
self.parser = parser
self.reset()
def interpret\_raw\_text(self, text):
self.input\_buffer.extend(self.parser.parse(text))
try:
self.interpret\_items(self.input\_buffer)
except IndexError:
print (" ... (incomplete)")
except LoopError:
print ("LoopError ... exiting")
sys.exit(1)
def interpret\_items(self, items):
for item in items:
if self.open\_loops:
self.interpret\_inside\_loop(item)
else:
self.interpret\_directly(item)
def interpret\_inside\_loop(self, item):
if item == self.parser.END:
self.open\_loops -= 1
if self.open\_loops == 0:
while self.cells\[self.index\]:
self.interpret\_items(self.loop)
return
elif item == self.parser.BEGIN:
if self.open\_loops < self.MAX\_NESTED\_LOOPS:
self.open\_loops += 1
else:
raise LoopError("Nesting maximum (%s) exceeded"
% self.MAX\_NESTED\_LOOPS)
self.loop.append(item)
def interpret\_directly(self, item):
if item == self.parser.END:
raise ValueError("End without begin")
elif item == self.parser.BEGIN:
self.open\_loops = 1
self.loop = \[\]
elif item in self.parser.primitives:
method = self.parser.primitives\[item\]
getattr(self, method)()
else:
print ("Unknown token '%s' - ignored") % (item, )
def interpret\_file(self, fname):
file = open(fname, 'r')
self.interpret\_raw\_text(file.read())
def interactive\_mode(self):
print ("Ook! and Brainfuck interpreter V1.0")
print ("Type '?' to display the status of the interpreter. ")
print ("Type 'b' to enter brainfuck mode. Empty input quits.")
while True:
inp = raw\_input("oo> ").strip()
if inp == "?":
print (self)
elif inp == "b":
print ("Entering brainfuck mode. Type 'o' to return to Ook!")
self.set\_parser(self.bf\_parser)
elif inp == "o":
print ("Entering Ook! mode. Type 'b' to return to brainfuck.")
self.set\_parser(self.ook\_parser)
elif inp == "":
print (self)
break
else:
self.interpret\_raw\_text(inp)
def \_\_repr\_\_(self):
rep = "\\n".join(\["Cells\\t\\t: %s",
"Raw output\\t: %s",
"ASCII output\\t: %s"\])
return rep % (list(self.cells),
" ".join(\[str(i) for i in self.output\_buffer\]),
self.as\_ascii())
def print\_usage():
print ("\\nUsage:")
print ("\\tInterpret Ook! : python ook.py -o <FILENAME>")
print ("\\tInterpret BrainFuck : python ook.py -b <FILENAME>")
print ("\\tInteractive mode: python ook.py -i\\n")
if \_\_name\_\_ == '\_\_main\_\_':
if len(sys.argv) < 2:
print\_usage()
elif len(sys.argv) == 2 and sys.argv\[1\] == "-i":
ook = Interpreter()
ook.interactive\_mode()
elif len(sys.argv) == 3:
if sys.argv\[1\] == "-b":
ook = Interpreter(ook\_mode=False)
ook.interpret\_file(sys.argv\[2\])
print (ook)
elif sys.argv\[1\] == "-o":
ook = Interpreter(ook\_mode=True)
ook.interpret\_file(sys.argv\[2\])
print (ook)
else:
print\_usage()
else:
print\_usage()
(11)标准银河字母

(12)简单替换密码

(二)编码
1.ASCII编码

2.Base编码
base64、32、16。。。
3.unicode编码
源文本: The
&#x \[Hex\]: The
&# \[Decimal\]: The
\\U \[Hex\]: \\U0054\\U0068\\U0065
\\U+ \[Hex\]: \\U+0054\\U+0068\\U+0065
4.url编码
例子:The quick
%54%68%65%20%71%75%69%63%6b
5.html编码
(1)普通html编码
特征:&# 开头 由 &# 开头,后面加数字
(2)html实体编码

6.rabbit编码
跟base64很像,但是需要密钥,Rabbit加密开头部分通常为U2FsdGVkX1
7.python反编译
EasyPythonDecompiler软件,1.pyc转1.py
8.quipquip词频分析
(三)现代密码学–对称加密
1.DES
2.AES
3.RC4
RC4包含两个算法: 1.密钥调度算法(KSA) 2.伪随机数生成算法(PRGA)
RC4是经典流密码之一,由于加密和解密使用相同的密钥,所以也是对称密码的一种。由于RC4存在弱点,现已禁止在TLS中使用RC4加解密算法。
RC4会根据明文长度将密钥扩展到与明文相同的长度,并遵从逐个字节加密的原则。加密的原理是异或。
def rc4\_init(s\_box, key, key\_len): # rc4初始化函数,产生s\_box
k = \[0\] \* 256
i = j = 0
for i in range(256):
s\_box\[i\] = i
k\[i\] = key\[i % key\_len\]
for i in range(256):
j = (j + s\_box\[i\] + ord(k\[i\])) % 256
s\_box\[i\], s\_box\[j\] = s\_box\[j\], s\_box\[i\]
def rc4\_crypt(s\_box, data, data\_len, key, key\_len): # rc4算法,由于异或运算的对合性,RC4加密解密使用同一套算法,加解密都是它
rc4\_init(s\_box, key, key\_len)
i = j = 0
for k in range(data\_len):
i = (i + 1) % 256
j = (j + s\_box\[i\]) % 256
s\_box\[i\], s\_box\[j\] = s\_box\[j\], s\_box\[i\]
t = (s\_box\[i\] + s\_box\[j\]) % 256
data\[k\] ^= s\_box\[t\]
if \_\_name\_\_ == '\_\_main\_\_':
s\_box = \[0\] \* 257 # 定义存放s\_box数据的列表
# 此处的data即要解密的密文,需要定义成列表形式,其中的元素可以是十六进制或十进制数
# 如果题目给出的是字符串,需要你自己先把数据处理成列表形式再套用脚本
data = \[0xB6,0x42,0xB7,0xFC,0xF0,0xA2,0x5E,0xA9,0x3D,0x29,0x36,0x1F,0x54,0x29,0x72,0xA8,0x63,0x32,0xF2,0x44,0x8B,0x85,0xEC,0xD,0xAD,0x3F,0x93,0xA3,0x92,0x74,0x81,0x65,0x69,0xEC,0xE4,0x39,0x85,0xA9,0xCA,0xAF,0xB2,0xC6\]
#key一定要字符串
key = "gamelab@"
rc4\_crypt(s\_box, data, len(data), key, len(key))
for i in data:
print(chr(i), end='')
(四)现代密码学–非对称加密
1.RSA


(1)基础已知p、q、e求d
#RSA---知道p、q、e求d
from Crypto.Util.number import \*
#gmpy2 是一个用于高精度数学运算的 Python 库,它提供了快速的大整数运算功能
import gmpy2
# 定义素数 p 和 q
p = 275127860351348928173285174381581152299
q = 319576316814478949870590164193048041239
# 计算模数 n
n = p \* q
# 计算欧拉函数 φ(n)
r = (p - 1) \* (q - 1)
# 选择公钥指数 e
e = 65537
# 计算私钥指数 d
d = gmpy2.invert(e, r)
# 打印私钥指数 d
print("私钥指数 d:", d)
(2)知道加密后的文本和公钥文本(就是知道了n、p、q、e、c求m)

step1:使用openssl解出e和n
openssl rsa -pubin -text -modulus -in warmup -in pubkey.pem

e=65537,n=Modulus的十六进制
step2:进制转换(16转10)
def hex\_to\_decimal(hex\_string):
try:
decimal\_num = int(hex\_string, 16)
return decimal\_num
except ValueError:
print("输入的不是有效的十六进制字符串。")
return None
hex\_str = "C2636AE5C3D8E43FFB97AB09028F1AAC6C0BF6CD3D70EBCA281BFFE97FBE30DD"
result = hex\_to\_decimal(hex\_str)
if result is not None:
print(f"转换为十进制是: {result}")
n=87924348264132406875276140514499937145050893665602592992418171647042491658461
step3:使用yafu分解n,得出p、q

step4:加密后的文本flag.enc的十六进制再转为十进制就是c


c=49412914049026066227292604633959399022586841904231599586841156187258952420473
step5:根据基础ras脚本解出m
from Crypto.Util.number import \*
import gmpy2
e=65537
p= 319576316814478949870590164193048041239
q= 275127860351348928173285174381581152299
n=p\*q
c = 49412914049026066227292604633959399022586841904231599586841156187258952420473
r=(p-1)\*(q-1)
d=gmpy2.invert(e,r)
m=pow(c,d,n)
print(m)
得到m=4865677769286717240419296208145914517832094464845949055035370987525602570
step6:m转为16进制,再转为ASCII码(这样更不容易出错,有些题会出现多一个字符的情况)
def decimal\_to\_hex(decimal\_num):
hex\_chars = "0123456789ABCDEF"
if decimal\_num == 0:
return '0'
hex\_str = ''
negative = False
if decimal\_num < 0:
negative = True
decimal\_num = -decimal\_num
while decimal\_num > 0:
remainder = decimal\_num % 16
hex\_str = hex\_chars\[remainder\] + hex\_str
decimal\_num //= 16
if negative:
hex\_str = '-' + hex\_str
return hex\_str
decimal\_num =4865677769286717240419296208145914517832094464845949055035370987525602570
hex\_result = decimal\_to\_hex(decimal\_num)
print(f"转换为十六进制是: {hex\_result}")

这种情况是多了一位,删去2

(3)知道加密后的文本和私钥文本
openssl rsautl -decrypt -in key.txt(加密后的文件) -inkey pub.key(私钥) -out flag.txt
(4)RSA共模攻击
所谓共模,就是明文m相同,模n相同,用两个公钥e1,e2加密得到两个私钥d1,d2和两个密文c1,c2 共模攻击,即当n不变的情况下,知道n,e1,e2,c1,c2 。可以在不知道d1,d2的情况下,解出m
import gmpy2
n=13060424286033164731705267935214411273739909173486948413518022752305313862238166593214772698793487761875251030423516993519714215306808677724104692474199215119387725741906071553437840256786220484582884693286140537492541093086953005486704542435188521724013251087887351409946184501295224744819621937322469140771245380081663560150133162692174498642474588168444167533621259824640599530052827878558481036155222733986179487577693360697390152370901746112653758338456083440878726007229307830037808681050302990411238666727608253452573696904083133866093791985565118032742893247076947480766837941319251901579605233916076425572961
c1=12847007370626420814721007824489512747227554004777043129889885590168327306344216253180822558098466760014640870748287016523828261890262210883613336704768182861075014368378609414255982179769686582365219477657474948548886794807999952780840981021935733984348055642003116386939014004620914273840048061796063413641936754525374790951194617245627213219302958968018227701794987747717299752986500496848787979475798026065928167197152995841747840050028417539459383280735124229789952859434480746623573241061465550303008478730140898740745999035563599134667708753457211761969806278000126462918788457707098665612496454640616155477050
c2=6830857661703156598973433617055045803277004274287300997634648800448233655756498070693597839856021431269237565020303935757530559600152306154376778437832503465744084633164767864997303080852153757211172394903940863225981142502888126928982009493972076013486758460894416710122811249903322437742241269681934551237431668187006176418124934488775505816544733929241927900392924886649420943699356314278255683484998359663404611236056664149725644051300950988495549164517140159041907329062655574220869612072289849679613024196448446224406889484578310512232665571188351621585528255501546941332782446448144033997067917984719103068519
e1=117
e2=65537
r,s1,s2 = gmpy2.gcdext(e1, e2)
m = (pow(c1,s1,n)\*pow(c2,s2,n)) % n
print(m)
(5)分解素数多于两个
攻防世界:baigeiRSA2
step1:分解n,素数为5个

step2:脚本
from Crypto.Util.number import \*
import gmpy2
e=65537
p=9401433281508038261
q=13716847112310466417
s=11215197893925590897
t=11855687732085186571
y=10252499084912054759
n=p\*q\*s\*t\*y
c =144009221781172353636339988896910912047726260759108847257566019412382083853598735817869933202168
r=(p-1)\*(q-1)\*(s-1)\*(t-1)\*(y-1)
d=gmpy2.invert(e,r)
m=pow(c,d,n)
print(m)
大体都一样,就是n=p_q_s_t_y,r=(p-1)(q-1)(s-1)(t-1)(y-1),这两个地方变了
(6)n分解出来就一个(即n是质数)
from Crypto.Util.number import \*
import gmpy2
e=65537
p= 2277984791022346369005533904783614818826102788659651508959767202083843778453131366658916382803461140562467908905967443285040501371560088604538394878005827646410146244954745505114406792711000349929611271710262426493710967674490536959788665890671796421985910748091011210709414415838780453626144971988788672588103654983
n=p
c = 415510106371698055042355817455792784402467839071261284227679808181073943762112386236619891503158397068812942349049185918370823556100880803528976860244812587012654626659823858350868438615582709075400040571632681052556974452098591809573228654622307014559692352778252371646024960520522510301144376842967556042367321117
r=(p-1)
d=gmpy2.invert(e,r)
m=pow(c,d,n)
print(m)
大体都一样,就是n=p,r=p-1
2.DH
3.ECC
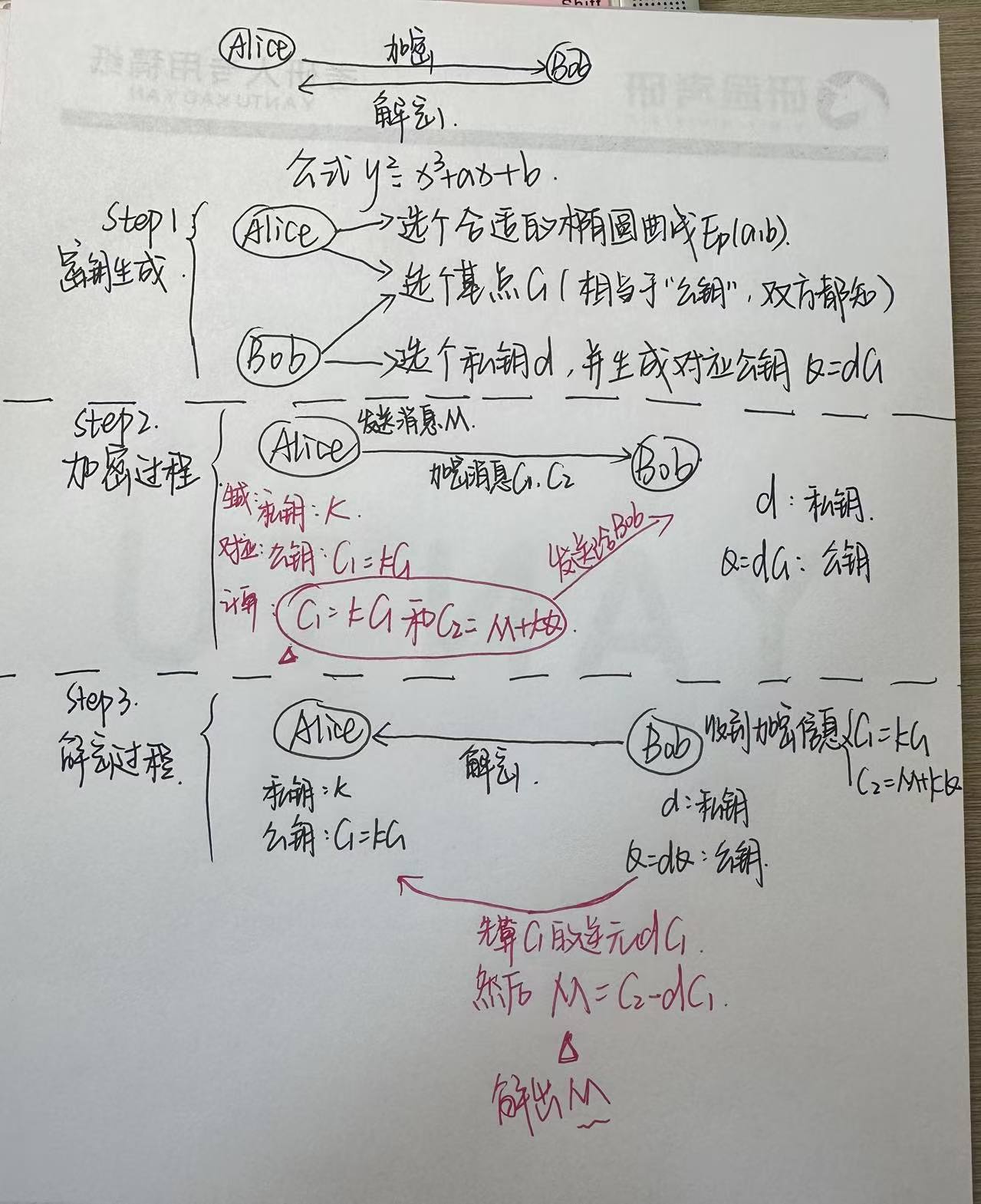
(1)椭圆曲线加密基础
知道p(有限特征值)、a、b、G(基点)、k(私钥),求公钥K,也就是上图的C1
import collections
import random
EllipticCurve = collections.namedtuple('EllipticCurve', 'name p a b g n h')
curve = EllipticCurve(
'secp256k1',
# Field characteristic.
p=int(input('p=')),
# Curve coefficients.
a=int(input('a=')),
b=int(input('b=')),
# Base point.
g=(int(input('Gx=')),
int(input('Gy='))),
# Subgroup order.
n=int(input('k=')),
# Subgroup cofactor.
h=1,
)
# Modular arithmetic ##########################################################
def inverse\_mod(k, p):
"""Returns the inverse of k modulo p.
This function returns the only integer x such that (x \* k) % p == 1.
k must be non-zero and p must be a prime.
"""
if k == 0:
raise ZeroDivisionError('division by zero')
if k < 0:
# k \*\* -1 = p - (-k) \*\* -1 (mod p)
return p - inverse\_mod(-k, p)
# Extended Euclidean algorithm.
s, old\_s = 0, 1
t, old\_t = 1, 0
r, old\_r = p, k
while r != 0:
quotient = old\_r // r
old\_r, r = r, old\_r - quotient \* r
old\_s, s = s, old\_s - quotient \* s
old\_t, t = t, old\_t - quotient \* t
gcd, x, y = old\_r, old\_s, old\_t
assert gcd == 1
assert (k \* x) % p == 1
return x % p
# Functions that work on curve points #########################################
def is\_on\_curve(point):
"""Returns True if the given point lies on the elliptic curve."""
if point is None:
# None represents the point at infinity.
return True
x, y = point
return (y \* y - x \* x \* x - curve.a \* x - curve.b) % curve.p == 0
def point\_neg(point):
"""Returns -point."""
assert is\_on\_curve(point)
if point is None:
# -0 = 0
return None
x, y = point
result = (x, -y % curve.p)
assert is\_on\_curve(result)
return result
def point\_add(point1, point2):
"""Returns the result of point1 + point2 according to the group law."""
assert is\_on\_curve(point1)
assert is\_on\_curve(point2)
if point1 is None:
# 0 + point2 = point2
return point2
if point2 is None:
# point1 + 0 = point1
return point1
x1, y1 = point1
x2, y2 = point2
if x1 == x2 and y1 != y2:
# point1 + (-point1) = 0
return None
if x1 == x2:
# This is the case point1 == point2.
m = (3 \* x1 \* x1 + curve.a) \* inverse\_mod(2 \* y1, curve.p)
else:
# This is the case point1 != point2.
m = (y1 - y2) \* inverse\_mod(x1 - x2, curve.p)
x3 = m \* m - x1 - x2
y3 = y1 + m \* (x3 - x1)
result = (x3 % curve.p,
-y3 % curve.p)
assert is\_on\_curve(result)
return result
def scalar\_mult(k, point):
"""Returns k \* point computed using the double and point\_add algorithm."""
assert is\_on\_curve(point)
if k < 0:
# k \* point = -k \* (-point)
return scalar\_mult(-k, point\_neg(point))
result = None
addend = point
while k:
if k & 1:
# Add.
result = point\_add(result, addend)
# Double.
addend = point\_add(addend, addend)
k >>= 1
assert is\_on\_curve(result)
return result
# Keypair generation and ECDHE ################################################
def make\_keypair():
"""Generates a random private-public key pair."""
private\_key = curve.n
public\_key = scalar\_mult(private\_key, curve.g)
return private\_key, public\_key
private\_key, public\_key = make\_keypair()
print("private key:", hex(private\_key))
print("public key: (0x{:x}, 0x{:x})".format(\*public\_key))
假设椭圆曲线方程为,发送方和接收方选取的私钥k=7,基点P为(0,1),假设发送方想要把一个数4发送给接收方,那么先将x=4带入曲线方程,得到明文M(4,4)。再根据k和P计算出公钥Q=7P=(42, 14),随机选一个数r=3,那么密文c= E(M)=(rP,M+rQ)=((19, 28), (6, 45))。
接收方知道了密文c和私钥k,只需要按照解密法则M=D©= M+rQ-krP就可以求出明文M(4,4)
#coding:gbk
p = 53
i = lambda x: pow(x, p-2, p)
def add(A, B):#加法运算
(u, v), (w, x) = A, B
assert u != w or v == x
if u == w: m = (3\*u\*w + 1) \* i(v+x)
else: m = (x-v) \* i(w-u)
y = m\*m - u - w
z = m\*(u-y) - v
return y % p, z % p
def opposite(A):#取A的相反数,也就是将A变成-A
return A\[0\],(-A\[1\])%p
def mul(t, A, B=0):#乘法运算
if not t:
return B
if t%2==0:
return mul(t//2, add(A,A), B)
elif B!=0:
return mul(t//2, add(A,A), add(B,A))
else:
return mul(t//2, add(A,A),A)
M=(4,4)
P=(0,1)
r=3
k=7
Q=mul(k,P)
c=(mul(r,P),add(M,mul(r,Q)))
print("公钥Q是",Q)
print("密文c是",c)
print("明文M是",add(c\[1\],opposite(mul(k,c\[0\]))))
(2)椭圆曲线数字签名
椭圆曲线数字签名算法,它利用椭圆曲线密码学(ECC)对数字签名算法(DSA)进行模拟,其安全性基于椭圆曲线离散对数问题。
但是当某些数值相同时会出现一些安全问题。 分析代码可以看出,存在随机数重复使用。具体来说,这段代码中签名的过程中使用了相同的随机数 k 来对不同的消息进行签名。这种情况下,可以通过分析两个相同 k 值对应的消息签名来恢复私钥 dA。
在 ECDSA 中,每次签名过程中都会使用一个随机数 k,以确保生成唯一的签名。然而,如果相同的随机数 k 被重复使用来对不同的消息进行签名,攻击者就有可能通过数学分析和推导计算出私钥 dA。
import sympy
from hashlib import sha1
from Cryptodome.Util.number import long\_to\_bytes , bytes\_to\_long
def calculate\_private\_key(r1, s1, s2, h1, h2, n):
# 计算k值
k = ((h1 - h2) \* sympy.mod\_inverse(s1 - s2, n)) % n
# 计算私钥dA
dA = (sympy.mod\_inverse(r1, n) \* (k \* s1 - h1)) % n
return dA
if \_\_name\_\_ == "\_\_main\_\_":
# 定义椭圆曲线的参数
n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
# 签名中的r1, s1, s2值
r1 = 4690192503304946823926998585663150874421527890534303129755098666293734606680
s1 = 111157363347893999914897601390136910031659525525419989250638426589503279490788
s2 = 74486305819584508240056247318325239805160339288252987178597122489325719901254
h1 = bytes\_to\_long(sha1(b'Hi.').digest())
h2 = bytes\_to\_long(sha1(b'hello.').digest())
private\_key = calculate\_private\_key(r1, s1, s2, h1, h2, n)
print(f'flag{{{private\_key}}}')
4.DSA
5.ElGamal
(五)国密
(六)用提取、删除、替换字符
grep -o '\[A-Z\]' 1.txt | tr -d '\\n' >>2.txt
sed -i -e 's/ZERO/0/g' -e 's/ONE/1/g' 2.txt
sed 's/v\[0-9\]\\+\\s\*=\\s\*//g' 1.txt | sed 's/u//g' | tr -d '\\n ' | tr ';' ',' > output.txt删除v1-v43、u、换行、替换;为,

(七)01或者AB这种相反面
带有相反面的,比如黑白这种,想到转换成二进制0101或者摩斯密码.-.-
或者培根密码
(八)Linux系统的 shadow 文件格式
特征:就是Linux的shadow文件格式。。。
工具:Kali Linux 中的 John
e.g.
root:$6$HRMJoyGA$26FIgg6CU0bGUOfqFB0Qo9AE2LRZxG8N3H.3BK8t49wGlYbkFbxVFtGOZqVIq3q
Q6k0oetDbn2aVzdhuVQ6US.:17770:0:99999:7:::
Linux的 /etc/shadow 文件存储了该系统下所有用户口令相关信息,只有 root 权限可以查看,用户口令是以 Hash + Salt 的形式保护的。 每个字段都用 “$” 或“:”符号分割; 第一个字段是用户名,如root ; 第二个字段是哈希算法,比如 6 代表SHA-512,1 代表 MD5; 第三个字段是盐,比如上面的 HRMJoyGA 第四个字段是口令+盐加密后的哈希值 后面分别是密码最后一次修改日期、密码的两次修改间隔时间(和第三个字段相比)、密码的有效期(和第三个字段相比)、密码修改到期前的警告天数(和第五个字段相比)、密码过期后的宽限天数(和第五个字段相比)、账号失效时间,这里不太重要要;
直接跑 John 试试
john shadow
如果解开了,加 --show 查看解密口令
john --show shadow
(九)MD5
特征:一般为16位或32位 ,由数字和小写字母组成
0906b080b03ea64d0534d36b2bd9edb8

黑客/网络安全学习包


资料目录
-
成长路线图&学习规划
-
配套视频教程
-
SRC&黑客文籍
-
护网行动资料
-
黑客必读书单
-
面试题合集
因篇幅有限,仅展示部分资料,需要点击下方链接即可前往获取
优快云大礼包:《黑客&网络安全入门&进阶学习资源包》免费分享
1.成长路线图&学习规划
要学习一门新的技术,作为新手一定要先学习成长路线图,方向不对,努力白费。
对于从来没有接触过网络安全的同学,我们帮你准备了详细的学习成长路线图&学习规划。可以说是最科学最系统的学习路线,大家跟着这个大的方向学习准没问题。

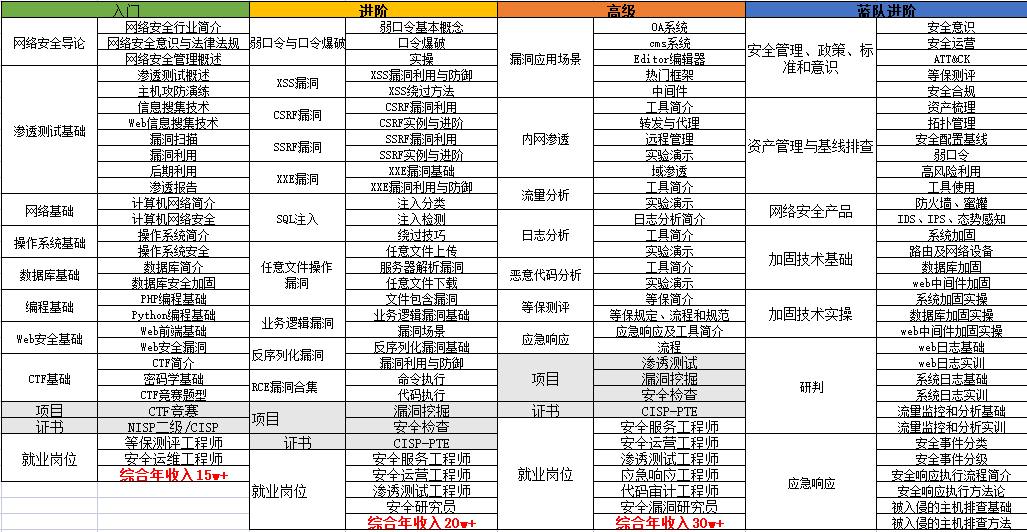
因篇幅有限,仅展示部分资料,需要点击下方链接即可前往获取
优快云大礼包:《黑客&网络安全入门&进阶学习资源包》免费分享
2.视频教程
很多朋友都不喜欢晦涩的文字,我也为大家准备了视频教程,其中一共有21个章节,每个章节都是当前板块的精华浓缩。
因篇幅有限,仅展示部分资料,需要点击下方链接即可前往获取
优快云大礼包:《黑客&网络安全入门&进阶学习资源包》免费分享
3.SRC&黑客文籍
大家最喜欢也是最关心的SRC技术文籍&黑客技术也有收录
SRC技术文籍:

黑客资料由于是敏感资源,这里不能直接展示哦!
4.护网行动资料
其中关于HW护网行动,也准备了对应的资料,这些内容可相当于比赛的金手指!
5.黑客必读书单
**

**
6.面试题合集
当你自学到这里,你就要开始思考找工作的事情了,而工作绕不开的就是真题和面试题。
更多内容为防止和谐,可以扫描获取~

因篇幅有限,仅展示部分资料,需要点击下方链接即可前往获取




















 8200
8200

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








