#SAS统计分析-参数估计与假设检验

印象中，关于参数估计与假设检验先前也是有写过一丢丢，想要回顾的可以点击：

由于有了之前的基础，今天的文章就会跳过一些比较简单的概念梳理与讲解，但是一些比较重要的点我还是会稍微提及一下下咯。

所谓统计推断，就是利用样本所提供的信息对总体的某些统计特征进行估计或者判断。一般分为参数估计和假设检验。

一、参数估计

假设总体的分布函数的类型已知，但其他的一个或多个参数未知，那么久需要对未知的参数进行合理的估计，并对估计结果进行评价，这样子的过程，称之为参数估计。

1. 点估计

又称之为定值估计，样本的均值可以用来估计总体均值，样本的标准差可以用来估计总体标准差，进行点估计的方法有很多，如矩估计法、最小二乘法、极大似然法等，sas中的proc步能够实现这些参数估计方法。

无偏性、有效性和一致性是衡量一个 参数估计好坏的基本标准。

2. 区间估计

对于未知参数，我们除了关心它的点估计，还希望估计出一个区间，并且希望这个参数落在这个区间的可信程度，这就是区间估计。

置信区间越短，表示估计的精度越高，反之则越低。通常情况下，我们希望提高置信水平，但，在样本容量一样的前提下，提高置信水平，必定会导致置信区间变宽。

实例：计算male的平均高度的99%置信区间。（数据集为sashelp中的class）

proc means data=sashelp.class  maxdec=2 n mean std stderr clm alpha=0.01; /*alpha= 是用来控制不同置信水平，alpha=0.01表示99%，alpha=0.05表示95%，默认是95%*/

    where sex="M";

    var height;

    title "99% confidence interval for male";

run;

二、假设检验

若已知总体分布函数的形式，但不了解其参数情况，又或者是对总体分布完全未知，为了总体的某些未知特征，先提出某些关于总体的假设，然后用适当的方法对样本进行计算，根据结果对假设做出接受或者拒绝，这一过程，就是假设检验。一般分为参数假设检验以及非参数假设检验。

1. 假设检验基本步骤

1）根据实际问题和已知信息，提出原假设和备择假设；

2）给定的显著性水平（犯弃真的概率）α；

3）收集整理数据；

4）根据已知的样本数据，计算出P值，做出是否拒绝H0的判断。（P>=α，接受原假设H0，P<α，拒绝原假设H0）

一个大的P值，表示在原假设H0为真的情况下，观测到该样本发生的概率很大，反之，则概率很小，我们就有足够的证据怀疑这一假设的真实性，从而拒绝原假设H0。

2. T分布与T检验

T检验又称为student T检验，只要样本满足正态性条件，就可以使用T检验进行均值比较。

正态性条件：

1）样本来自正态分布总体；

2）样本容量足够大，但如果样本是对称分布，样本容量达到30即可。

T检验分类：

一般分为单样本均值T检验和双样本均值T检验。前者用于检验一个样本均值与一个已知的总体均值的差异是否显著，后者用于检验两个样本各自所代表的总体的均值的差异是否显著。

双样本均值T检验又分为：独立双样本均值T检验和配对样本均值T检验，后续展开讲解。

实例：检验class中female的平均身高是否等于165cm

/*实例：检验class中female的平均身高是否等于165cm*/

proc univariate data=sashelp.class mu0=165;/*mu0= 是用来指定位置检验中原假设的总体均值*/

where sex="F";

var height;

title "testing whether the mean of female height=165";

run;

/*从下图可看出，P值远小于0.0001，即便在显著性水平为0.01下，仍小于，所以就拒绝原假设，可以认为有显著差异*/

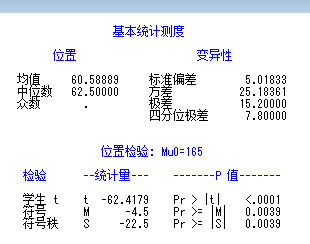
由于今晚有其他事情做，就先更新那么多吧，明天继续更新TTEST过程、单双样本均值T检验等，敬请期待！

”欢迎关注，嘻嘻~”