
? 温故而知新
? 今日份挑战
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票),设计一个算法来计算你所能获取的最大利润。
注意你不能在买入股票前卖出股票。
示例 1:
输入: [7,1,5,3,6,4]输出: 5解释: 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。 注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
示例 2:
输入: [7,6,4,3,1]输出: 0解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
先思考一下,后面我会给出一个解题思路~?

这道题我们明确知道交易只可以进行一次,所以,我们只要找到两个卖出和买入点的最大差值即可,这里有一个简单的公式:
最大利润=max{前一天最大利润, 今天的价格 - 之前最低价格}
Python实现1:
# 买卖股票的最佳时机
def maxProfit(prices):
if len(prices)<=1: return 0
price_min = prices[0]
profit_max = 0
for price in prices:
price_min = min(price_min, price)
profit_max = max(profit_max, price-price_min) # 最大利润=max{前一天最大利润, 今天的价格 - 之前最低价格}
return profit_max
下面呢,我根据自己的学习,整理了一下解题思路。
这里主要是用到了动态规划的思想,首先,先了解一下动态规划:
动态规划(dynamic programming)是运筹学的一个分支,是求解决策过程(decision process)最优化的数学方法。
动态规划一般可分为线性动规,区域动规,树形动规,背包动规四类。
举例:
线性动规:拦截导弹,合唱队形,挖地雷,建学校,剑客决斗等;
区域动规:石子合并, 加分二叉树,统计单词个数,炮兵布阵等;
树形动规:贪吃的九头龙,二分查找树,聚会的欢乐,数字三角形等;
背包问题:01背包问题,完全背包问题,分组背包问题,二维背包,装箱问题,挤牛奶(同济ACM第1132题)等;
而我们今天的解题思路只是其中一类,算是给还没有入门DP的同学一个案例。
这里的DP,你可以理解是一个框架,一个套路,如果遇到类似的问题,就可以套这个框架来解决问题,所以,我先介绍一下这个框架,然后再用今天的算法题来应用一下这个框架。
1、状态枚举
什么是状态?状态在这里的意思就是条件,比如这道股票交易的题目,条件就包括了:交易天数n、最大交易次数K、股票持有状态(0代表未持有,1代表持有)。每种“状态”,都有对应的“选择”,这道题的“选择”有:买入、卖出、无操作,我们用 buy, sell, rest 表示这三种选择。上面的东西,我们可以用一个三维列表来表示:
dp[i][k][0 or 1]
0 <= i <= n-1, 1 <= k <= K
n 为天数,大 K 为最多交易数此问题共 n × K × 2 种状态,全部穷举就能搞定。
for 0 <= i < n:
for 1 <= k <= K:
for s in {0, 1}:
dpi[s] = max(buy, sell, rest)
而且,上面抽象的切片,我们也可以用自然语言来表达,比如:
dp[3][2][1],代表今天是第三天,我现在手上持有着股票,至今最多进行 2 次交易。
dp[2][3][0],代表今天是第二天,我现在手上没有持有股票,至今最多进行 3 次交易。
2、状态转移
这道题可以画一下状态转移图:
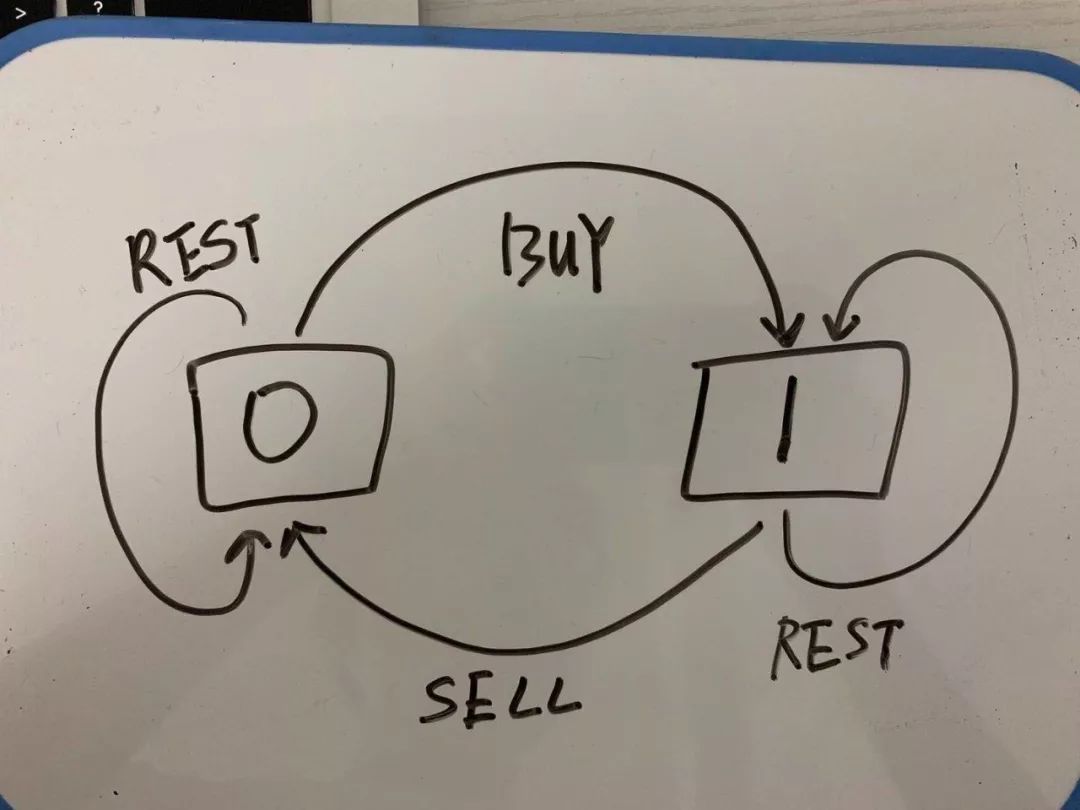
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
当前的股票持有状态为0,因此它的前一种状态可以是:
股票持有状态为0,选择rest
股票持有状态为1,选择sell,因为sell了,所以要加上利润prices[i]
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
当前的股票持有状态为1,因此它的前一种状态可以是:
股票持有状态为1,本次选择rest
股票持有状态为0,本次选择buy,因为buy了,所以要减去成本prices[i],同时,交易次数要减去1
当然,还有一些特殊情况需要单独处理:
dp[-1][k][0] = 0
解释:因为 i 是从 0 开始的,所以 i = -1 意味着还没有开始,这时候的利润当然是 0 。
dp[-1][k][1] = -infinity
解释:还没开始的时候,是不可能持有股票的,用负无穷表示这种不可能。
dp[i][0][0] = 0
解释:因为 k 是从 1 开始的,所以 k = 0 意味着根本不允许交易,这时候利润当然是 0
dp[i][0][1] = -infinity
解释:不允许交易的情况下,是不可能持有股票的,用负无穷表示这种不可能。
总结一下,状态转移方程如下:
dp[-1][k][0] = dp[i][0][0] = 0
dp[-1][k][1] = dp[i][0][1] = -infinity
状态转移方程:
dp[i][k][0] = max(dp[i-1][k][0], dp[i-1][k][1] + prices[i])
dp[i][k][1] = max(dp[i-1][k][1], dp[i-1][k-1][0] - prices[i])
细心的同学可能会发现上面的结构其实有点“越界”问题,比如i=0时候,i-1其实是非法的,因此,我们需要对一些边界情况做一下处理。
对于这道题,交易次数为1,因此K=1,代入状态转移方程:
dp[i][1][0] = max(dp[i-1][1][0], dp[i-1][1][1] + prices[i])
dp[i][1][1] = max(dp[i-1][1][1], dp[i-1][0][0] - prices[i])
因为k = 0,所以 dp[i-1][0][0] = 0,因此,
dp[i][1][0] = max(dp[i-1][1][0], dp[i-1][1][1] + prices[i])
dp[i][1][1] = max(dp[i-1][1][1], -prices[i])
现在发现 k 都是 1,不会改变,即 k 对状态转移已经没有影响了,可以进行进一步化简去掉所有 k:
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], -prices[i])
Python实现 02:
# 买卖股票的最佳时机
def maxProfit(prices):
n = len(prices)
# 生成一个空状态机
dp = [[0]*2]*n
for i in range(n):
if i-1<0:
dp[i][0] = 0
dp[i][1] = -prices[i]
'''
dp[i][0] = max(dp[-1][0], dp[-1][1] + prices[i])
= max(0, -infinity + prices[i]) = 0
dp[i][1] = max(dp[-1][1], dp[-1][0] - prices[i])
= max(-infinity, 0 - prices[i])
= -prices[i]
'''
else:
dp[i][0] = max(dp[i-1][0], dp[i-1][1]+prices[i])
dp[i][1] = max(dp[i-1][1], -prices[i])
return dp[n-1][0]
? 配图角色背景介绍
原本是一名优秀的神经外科医生,因车祸导致其双手无法使用手术刀正常工作,之后来到喜马拉雅山上拜魔法师古一为师,成为强大的魔法师,看家法器是一件有自我意识的悬浮斗篷。
性格高傲的神经外科手术专家史蒂芬·斯特兰奇(本尼迪克特·康伯巴奇饰)事业有成,在遭遇一次车祸悲剧后,双手再也无法握住手术刀,不能继续他的医生职业,为了治疗他的伤,他远赴尼泊尔遇到了莫度男爵(切瓦特·埃加福特饰),在莫度男爵带动下他得到古一法师(蒂尔达·斯文顿饰)帮助。斯蒂芬-斯特兰奇把自己曾经的自负都抛在了一边,开始接触和学习鲜为人知的玄学,以及多维空间世界的学问。在纽约的格林威治村,变身奇异博士的斯特兰奇,现实世界和多维空间的中间人,他利用超自然能力和神器来保护着世界,更要与力量强大党羽众多的卡西利亚斯(麦斯·米科尔森饰)一决高下,来拯救即将崩塌的多维世界。




















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








