Leetcode367. 有效的完全平方数

最新推荐文章于 2024-10-18 23:54:19 发布

原创最新推荐文章于 2024-10-18 23:54:19 发布 · 296 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #动态规划 #算法

Every day a LeetCode 专栏收录该内容

550 篇文章

订阅专栏

这篇博客探讨了有效完全平方数的四种不同计算方法，包括直接使用sqrt函数、暴力遍历、二分搜索以及数学公式。每种方法都有其优缺点，例如sqrt方法简洁但可能损失精度，暴力法简单但效率较低，二分搜索在效率和准确性间取得平衡，数学公式法巧妙但适用范围有限。这些解法展示了在算法设计中如何权衡效率和复杂性。

Every day a leetcode

题目来源：367. 有效的完全平方数

解法1：用sqrt

代码：

bool isPerfectSquare(int num){
    if((int)(sqrt(num))*sqrt(num) == num) return true;
    else return false;
}

结果：
在这里插入图片描述

解法2：暴力

注意用long，int会爆。
在这里插入图片描述

代码：

bool isPerfectSquare(int num){
    long x=1;
    long n=1;
    while(n<=num)
    {
        if(n == num) return true;
        x++;
        n=x*x;
    }
    return false;
}

结果：
在这里插入图片描述

解法3：二分搜索

代码：

bool isPerfectSquare(int num){
    int left=1;
    int right=num;
    long mid;
    while(left<=right)
    {
        mid=left+(right-left+1)/2;
        long n=mid*mid;
        if(n == num) return true;
        else if(n<num) left=mid+1;
        else right=mid-1;  
    }
    return false;
}

结果：
在这里插入图片描述

解法4：数学

对于任一完全平方数，它可以展开为：

n^2 = 1+3+5+...+2*n-1

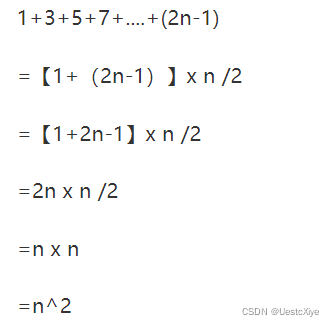
在这里插入图片描述

代码：

bool isPerfectSquare(int num){
    int x=1;
    while(num>0)
    {
        num-=x;
        x+=2;
    }
    if(num == 0) return true;
    else return false;
}