LeetCode 52 N皇后II_如何判断两个棋子是否出于一个对角线或反对教学-优快云博客

本文链接：https://blog.youkuaiyun.com/ProgramMonika/article/details/82705799

本文深入探讨了N皇后问题的解决策略，通过详细的步骤分解和代码实现，展示了如何使用递归和深度优先搜索来计算N皇后问题的不同解法数量。文章提供了清晰的算法思路，包括棋子的合法放置条件和递归搜索过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

LeetCod 52

              N皇后II

首先，先看一下题目：
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

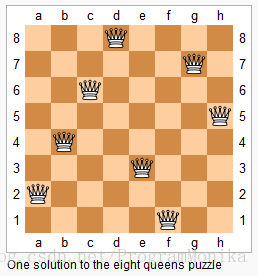
这里写图片描述
上图为 8 皇后问题的一种解法。

给定一个整数 n，返回 n 皇后不同的解决方案的数量。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
* 输入: 4
输出: [
[“.Q..”, // 解法 1
“…Q”,
“Q…”,
“..Q.”],

[“..Q.”, // 解法 2
“Q…”,
“…Q”,
“.Q..”]
]

解释: 4 皇后问题存在两个不同的解法。

思路1：

Step1    放置棋子
* 由于棋子不能放在同一行，所以按行放置

Step2    判断棋子是否合法
* 判断当前列是否有棋子，所在对角线是否有棋子

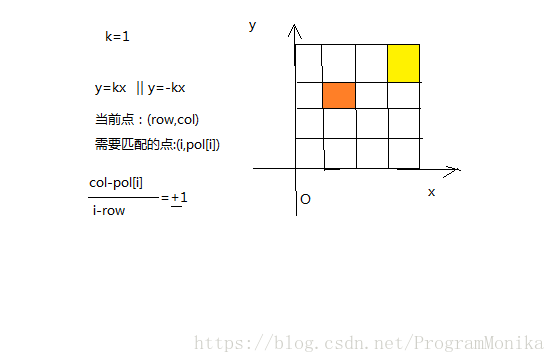
Step3    循环上面两步，并且判断棋子是否放完，每放完一次下次先要判断是否放完
* 判断要放的行是否走出了棋盘

class Solution {
public:
    int totalNQueens(int n) {
        vector<int> pol(n,-1);
        dfsNQ(pol,0); 
        return count;
    }
    int count=0;
    void dfsNQ(vector<int> pol,int row){
        int n=pol.size();
        if(row==n){
            count++;
        }else{
            for(int i=0;i<n;i++)
            {
                if(isPlace(pol,row,i))
                {
                    pol[row]=i;
                    dfsNQ(pol,row+1);
                }
            }
        }   
    }
    bool isPlace(vector<int> pol,int row,int col)
    {
        for(int i=0;i<row;i++)
        {
            if(pol[i]==col||abs(row-i)==abs(col-pol[i]))
            return false;
        }
        return true;
    }
};