论文全名:Deep Neural Solver for Math Word Problems
模型没有官方简称,但在(2020 COLING) Solving Math Word Problems with Multi-Encoders and Multi-Decoders 中被简称为DNS
论文链接:https://aclanthology.org/D17-1088/
本文是2017年EMNLP论文,关注MWP问题。
是第一篇用神经网络解决MWP问题的论文,直接将问题用RNN映射为公式。然后用结合RNN和基于相似度的检索模型,当检索模型相似度得分高于阈值时用检索结果的公式模版,反之用RNN。
文章目录
1. 背景


简介部分别的懒得看了。
有一点比较有趣的引用是 (2016 ACL) How well do Computers Solve Math Word Problems? Large-Scale Dataset Construction and Evaluation发现简单的基于相似度的方法就已经能超过大多数统计学习模型了。
2. 模型

numer mapping→number identification→检索→直接应用公式模版或用seq2seq模型
一些模型超参细节懒得写了,还是挺常规一RNN的。
变量: V p = { v 1 , … , v m , x 1 , … , x k } V_p=\{v_1,\dots,v_m,x_1,\dots,x_k\} Vp={v1,…,vm,x1,…,xk}(已知数字和未知变量)
2.1 数据预处理
number mapping
将公式映射到公式模版:将已知数字替换为number tokens
significant number identification
考虑到不是所有的数字都用得到,所以只关注重要数字:用LSTM进行二分类(输入是数字和上下文)

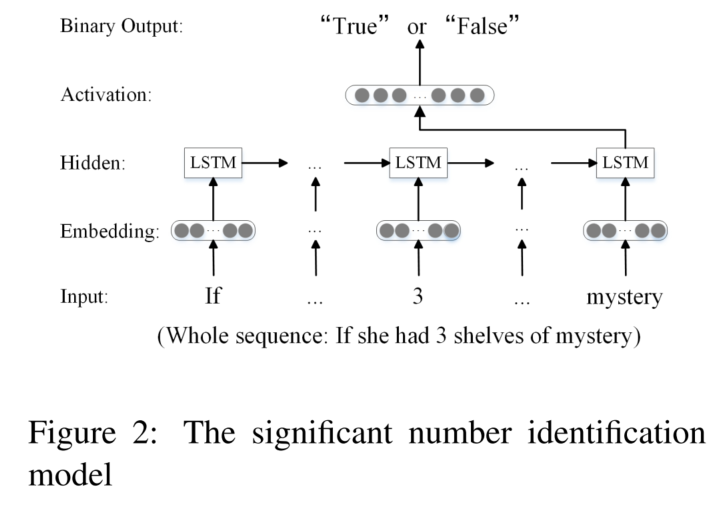
2.2 RNN based Seq2seq Model
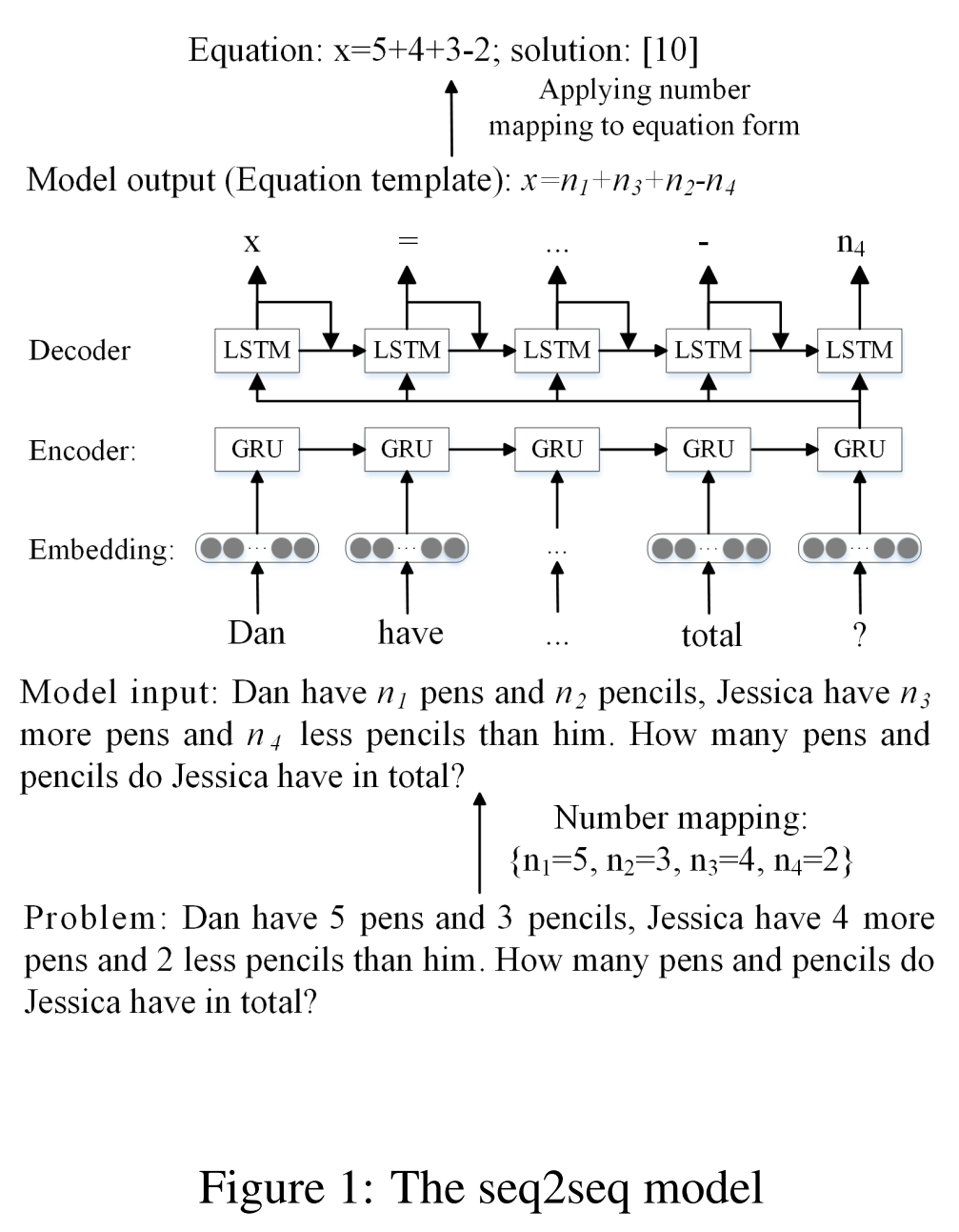
编码和解码分别用GRU和LSTM
激活函数直接用softmax的话,会导致出现非法符号。所以根据之前生成的公式判断非法字符,这根据预定义规则实现:
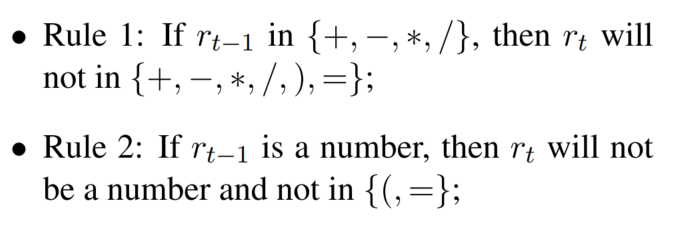
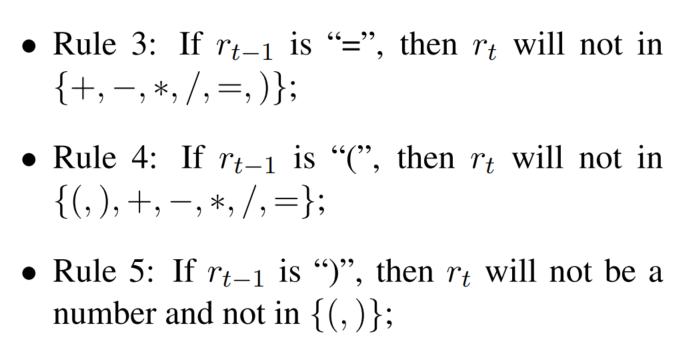
ρ
\rho
ρ是一个向量,每个元素都是0或1,代表字符是否在数学上正确(或者说符合上述规则):

基于LSTM解码器输出→生成字符 的概率
2.3 hybrid model
两种模型的正确比例:
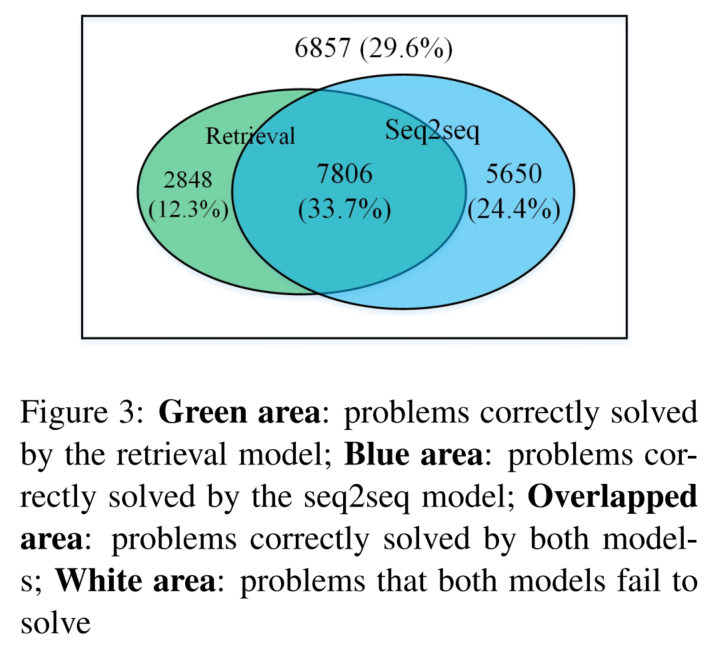
2.3.1 检索模型
计算样本和所有训练集样本之间的lexical similarity
对问题进行表征:词TF-IDF得分
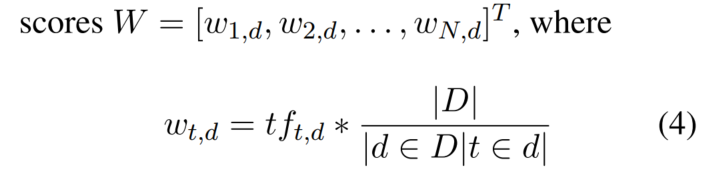
相似度是TF-IDF向量的Jaccard相似度: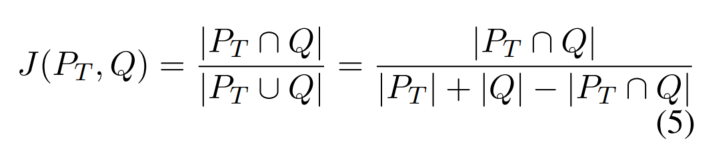
有一项observation是相似度阈值与2个模型准确率之间的关联(
θ
\theta
θ是阈值,即相似度大于阈值的我们用这个检索模型):

3. 实验
3.1 数据集
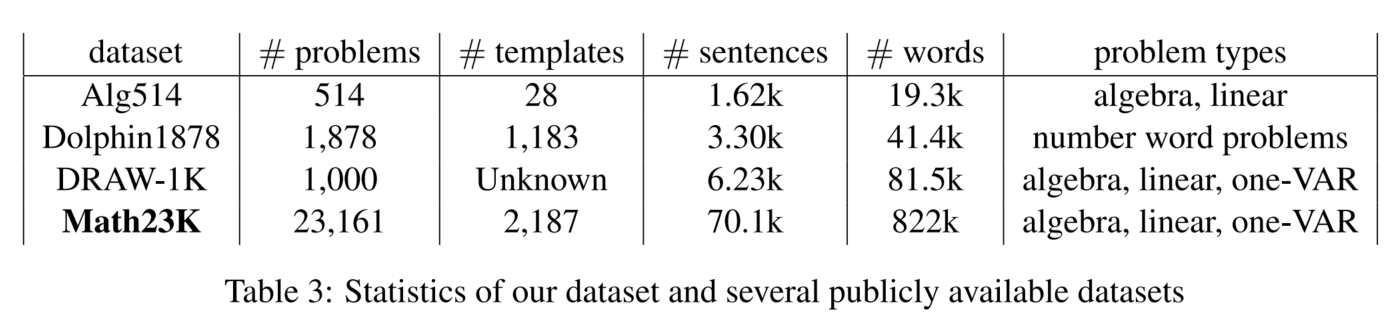
3.2 baseline
纯检索模型
ZDC
KAZB太大了,没法试
3.3 主实验结果
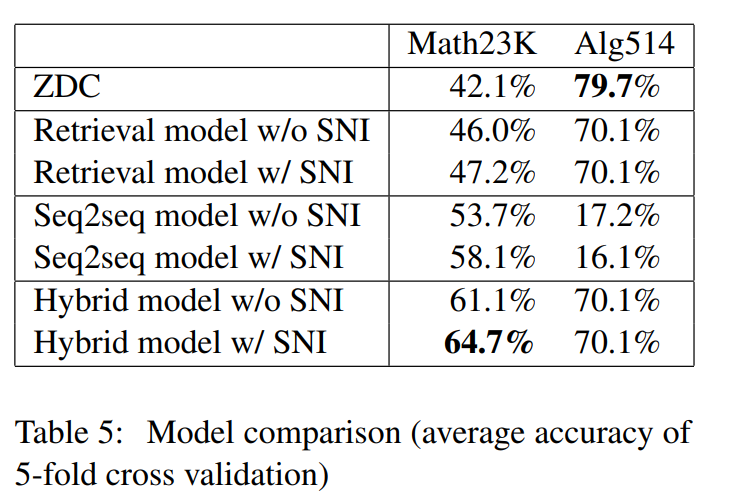
3.4 实验分析
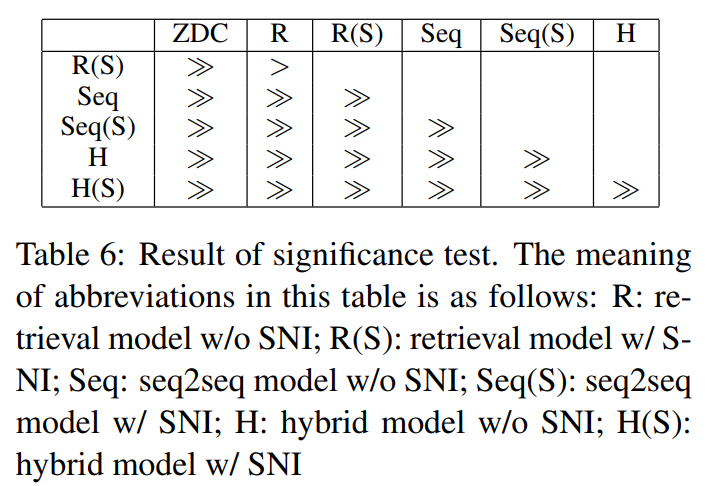
大于号指的是行大于列
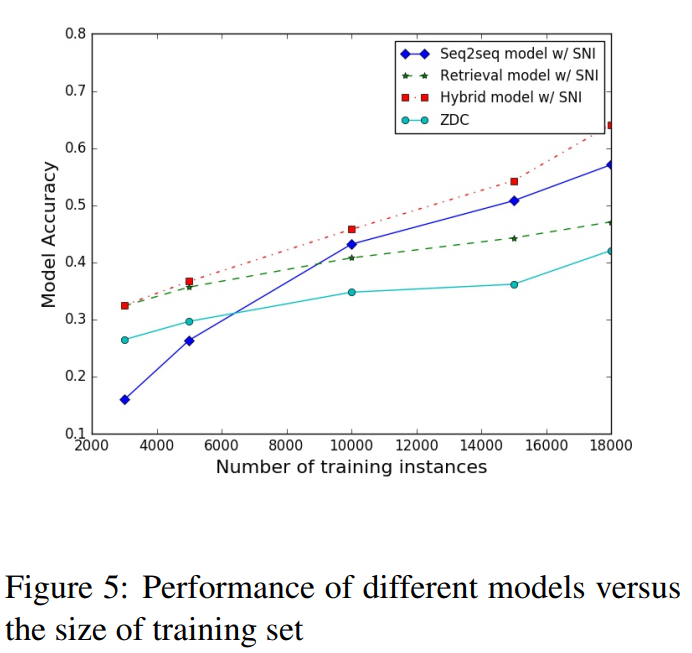
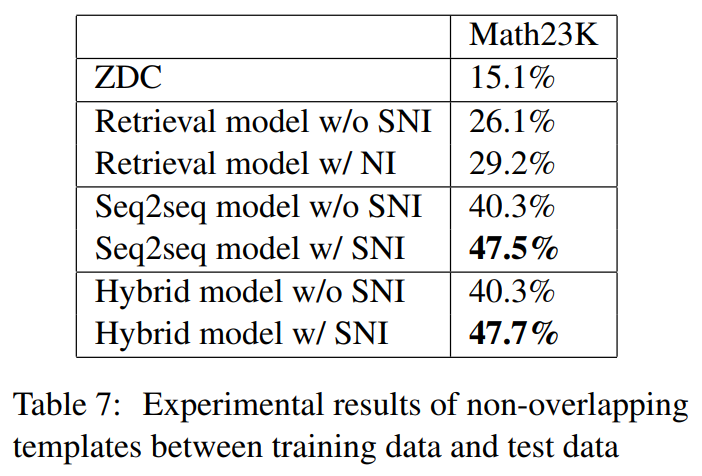





 该论文介绍了首次使用神经网络解决MathWordProblems的尝试,通过RNN序列到序列模型和检索模型的混合方法。数据预处理包括numbermapping和significantnumberidentification。模型在达到特定相似度阈值时选择使用检索结果或RNN生成公式。实验表明,这种混合模型在解决数学文字问题上表现优越。
该论文介绍了首次使用神经网络解决MathWordProblems的尝试,通过RNN序列到序列模型和检索模型的混合方法。数据预处理包括numbermapping和significantnumberidentification。模型在达到特定相似度阈值时选择使用检索结果或RNN生成公式。实验表明,这种混合模型在解决数学文字问题上表现优越。

















 1535
1535

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










