文章目录
YouTube视频观看地址1 视频观看地址2 视频观看地址3 视频观看地址4
本章主要内容:
首先介绍了深度图生成模型的基本情况,然后介绍了直接从图数据集中学习的GraphRNN模型1,最后介绍了医药生成领域的GCPN模型2。
1. Deep Generative Models for Graphs
对深度图生成模型,有两种看待问题的视角:
第一种是说,图生成任务很重要,我们此前已经学习过传统图生成模型3,接下来将介绍在图表示学习框架下如何用深度学习的方法来实现图生成任务。
另一种视角是将其视为图表示学习任务的反方向任务。
课程此前学习过的图表示学习任务4 deep graph encoders:输入图数据,经图神经网络输出节点嵌入
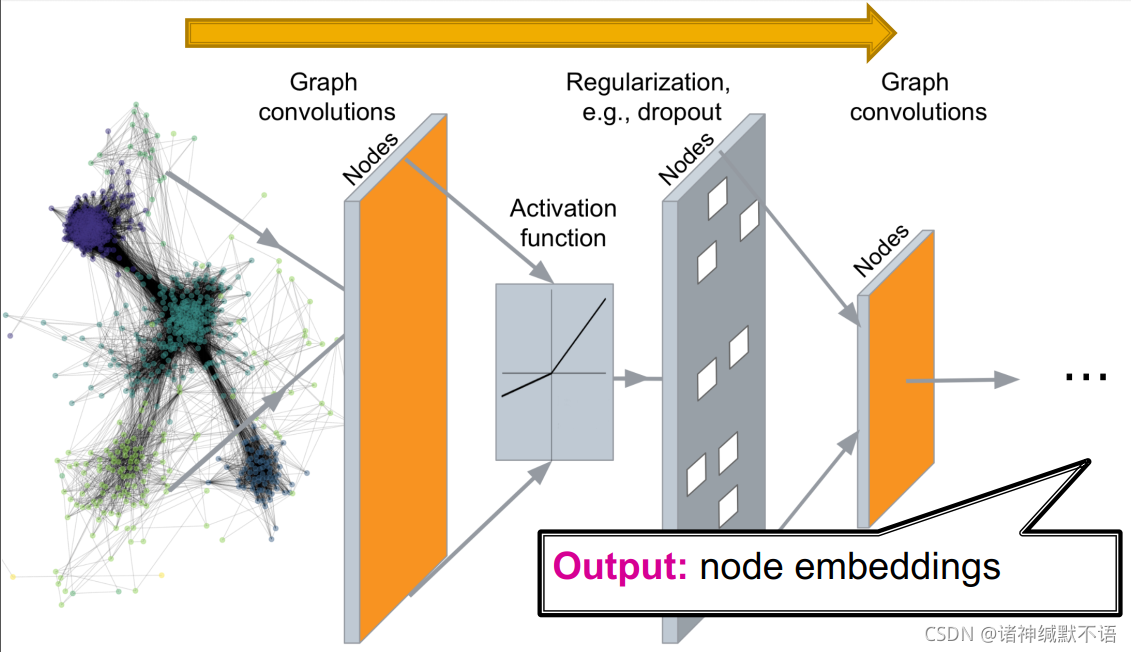
而深度图生成模型可以说是deep graph decoders:输入little noise parameter或别的类似东西,输出图结构数据
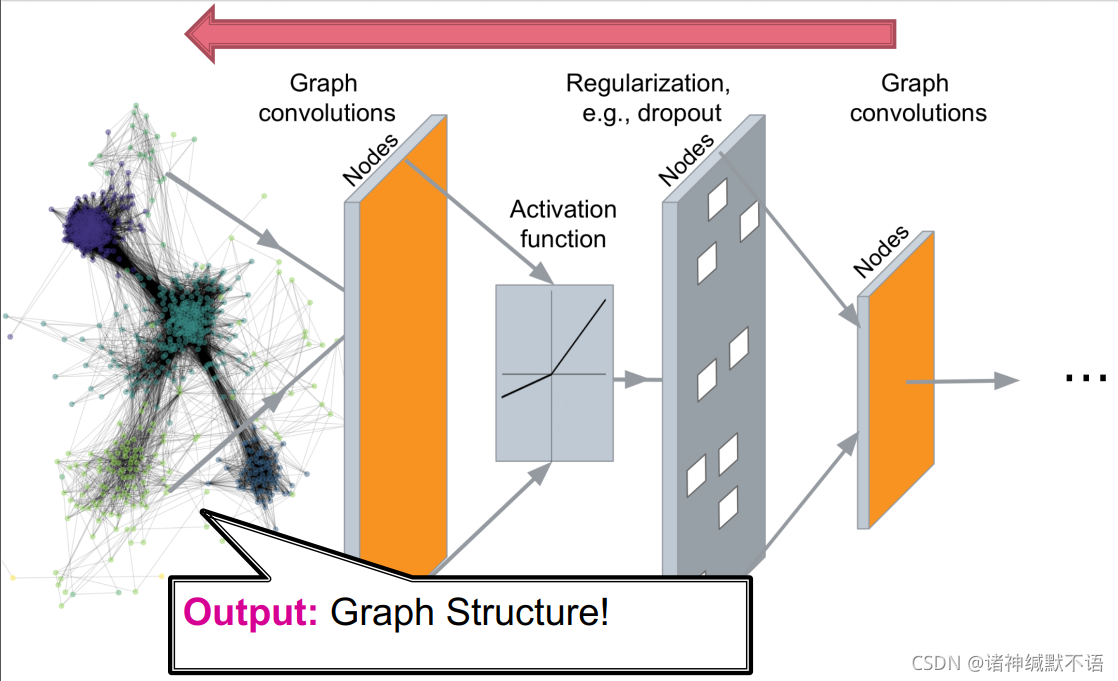
2. Machine Learning for Graph Generation
- 图生成任务分为两种:
- realistic graph generation
生成与给定的一系列图相似的图(本章2、3节重点) - goal-directed graph generation
生成优化特定目标或约束的图(举例:生成/优化药物分子)(本章第4节介绍)

- realistic graph generation
- 图生成模型
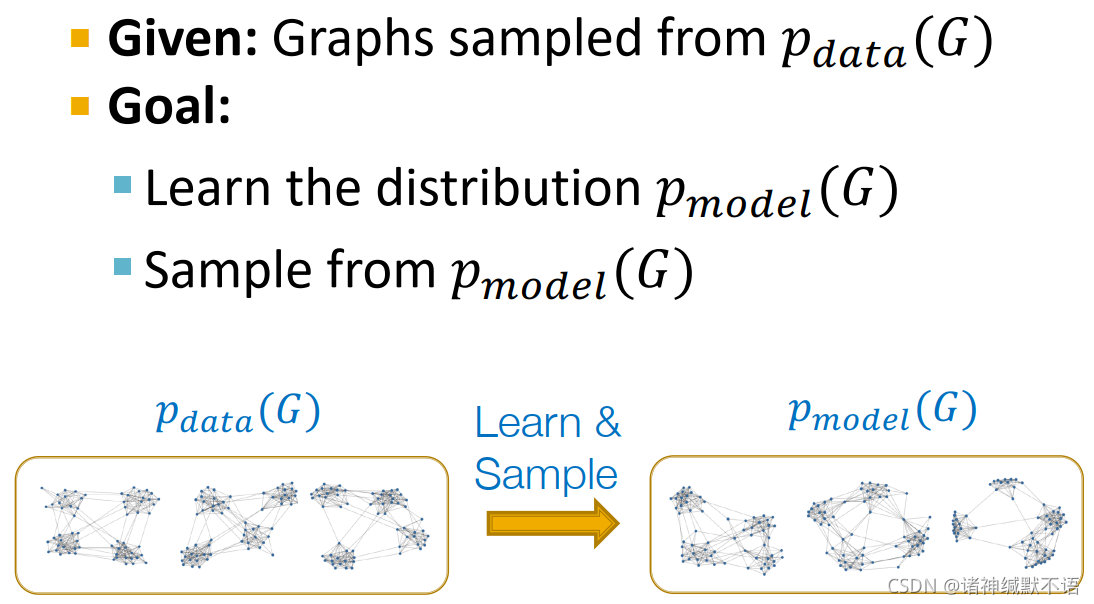
给定一系列图(抽样自一个冥冥中注定的数据分布 p d a t a ( G ) p_{data}(G) pdata(G))
目标:- 学到分布 p m o d e l ( G ) p_{model}(G) pmodel(G)
- 从
p
m
o
d
e
l
(
G
)
p_{model}(G)
pmodel(G) 中抽样,得到新的图
- 生成模型基础
我们想从一系列数据点(如图数据) { x i } \{\mathbf{x}_i\} {xi} 中学到一个生成模型:
p d a t a ( x ) p_{data}(\mathbf{x}) pdata(x) 是数据分布,不可知,但我们已经抽样出了 x i ∼ p d a t a ( x ) \mathbf{x}_i\sim p_{data}(\mathbf{x}) xi∼pdata(x)。
p m o d e l ( x ; θ ) p_{model}(\mathbf{x};\theta) pmodel(x;θ) 是模型,以 θ \theta θ 为参数,用于近似 p d a t a ( x ) p_{data}(\mathbf{x}) pdata(x) 。
学习目标:- density estimation: 使 p m o d e l ( x ; θ ) p_{model}(\mathbf{x};\theta) pmodel(x;θ) 近似 p d a t a ( x ) p_{data}(\mathbf{x}) pdata(x)
- sampling: 从
p
m
o
d
e
l
(
x
;
θ
)
p_{model}(\mathbf{x};\theta)
pmodel(x;θ) 中抽样,生成数据(图)

- density estimation
使 p m o d e l ( x ; θ ) p_{model}(\mathbf{x};\theta) pmodel(x;θ) 近似 p d a t a ( x ) p_{data}(\mathbf{x}) pdata(x)
主要原则:极大似然5 (建模分布的基本方法)
θ ∗ = arg max θ E x ∼ p d a t a log p m o d e l ( x ; θ ) \theta^*=\argmax_\theta\mathbb{E}_{x\sim p_{data}}\log{p_{model}(\mathbf{x};\theta)} θ∗=θargmaxEx∼pdatalogpmodel(x;θ)
即找到使被观察到的数据点 x i ∼ p d a t a \mathbf{x}_i\sim p_{data} xi∼pdata 最有可能在 p m o d e l p_{model} pmodel 下生成(即 ∏ i p m o d e l ( x i ; θ ∗ ) \prod_i{p_{model}(\mathbf{x}_i;\theta^*)} ∏ipmodel(xi;θ∗) 最大,即 log ∏ i p m o d e l ( x i ; θ ∗ ) \log{\prod_i{p_{model}(\mathbf{x}_i;\theta^*)}} log∏ipmodel(xi;θ∗) 最大,即 ∑ i log p m o d e l ( x i ; θ ∗ ) \sum_i\log{p_{model}(\mathbf{x}_i;\theta^*)} ∑ilogpmodel(xi;θ∗) 最大)的 p m o d e l p_{model} pmodel 的参数 θ ∗ \theta^* θ∗

- sampling
从 p m o d e l ( x ; θ ) p_{model}(\mathbf{x};\theta) pmodel(x;θ) 中抽样
从复杂分布中抽样的常用方法:
首先从一个简单noise distribution6 N ( 0 , 1 ) N(0,1) N(0,1) 中抽样出 z i \mathbf{z}_i zi
然后将 z i \mathbf{z}_i zi expand到图数据上,即将它通过函数 f ( ⋅ ) f(\cdot) f(⋅) 进行转换: x i = f ( z i ; θ ) \mathbf{x}_i=f(\mathbf{z}_i;\theta) xi=f(zi;θ),这样 x i \mathbf{x}_i xi 就能服从于一个复杂的分布。
f ( ⋅ ) f(\cdot) f(⋅) 通过已知数据,用深度神经网络进行学习。

- auto-regressive models
p m o d e l ( x ; θ ) p_{model}(\mathbf{x};\theta) pmodel(x;θ) 同时用于density estimation和sampling。
(一些其他模型,如Variational Auto Encoders (VAEs), Generative Adversarial Nets (GANs) 有二至多个模型来分别完成任务)
核心思想:链式法则。
联合分布是条件分布的连乘结果:
p m o d e l ( x ; θ ) = ∏ t = 1 n p m o d e l ( x t ∣ x 1 , … , x t − 1 ; θ ) p_{model}(\mathbf{x};\theta)=\prod_{t=1}^np_{model}(x_t|x_1,\dots,x_{t-1};\theta) pmodel(x;θ)=t=1∏npmodel(xt∣x1,…,xt−1;θ)
例如:如果 x \mathbf{x} x 是向量, x t x_t xt 是其第 t t t 维元素; x \mathbf{x} x 是句子, x t x_t xt 是其第 t t t 个单词。
在我们的案例中, x t x_t xt 是第 t t t 个行动(如增加一个节点或增加一条边)

3. GraphRNN: Generating Realistic Graphs
-
GraphRNN的优点在于它不需要任何inductive bias assumptions,就可以直接实现图生成任务。
-
GraphRNN的思想:sequentially增加节点和边,最终生成一张图。如图所示:
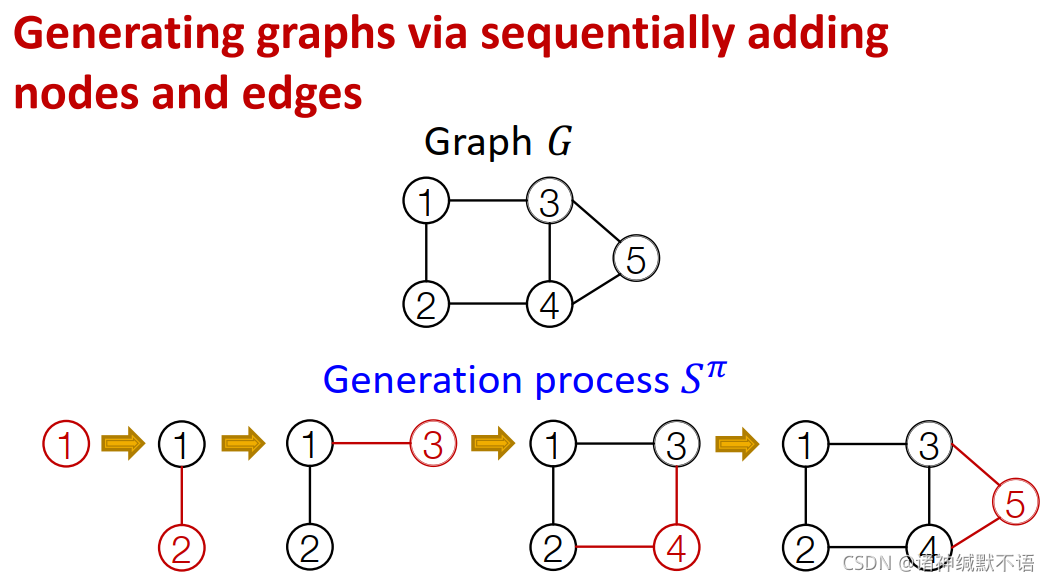
-
将图建模为序列:
给定图 G G G 及其对应的node ordering π \pi π,我们可以将其唯一映射为一个node and edge additions的序列 S π S^\pi Sπ
如图所示,序列 S π S^\pi Sπ 的每个元素都是加一个节点和这个节点与之前节点连接的边:
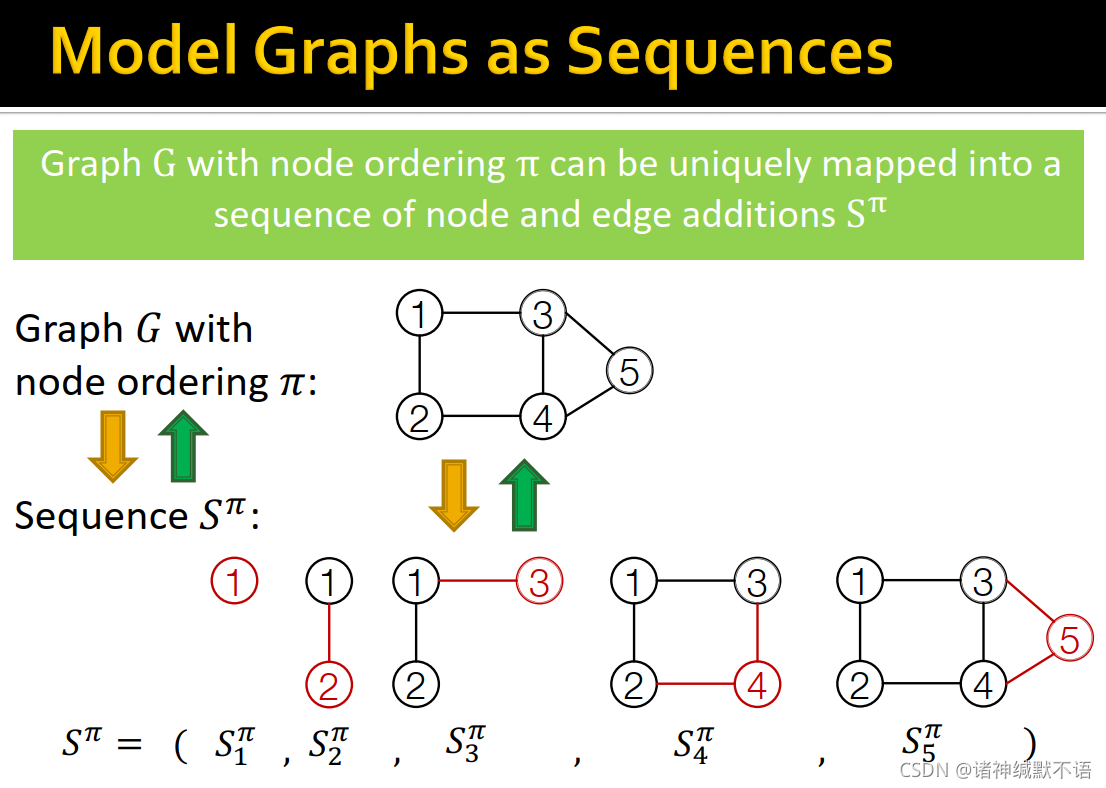
S π S^\pi Sπ 是一个sequence的sequence,有两个级别:节点级别每次添加一个节点,边级别每次添加新节点与之前节点之间的边。
节点级别:
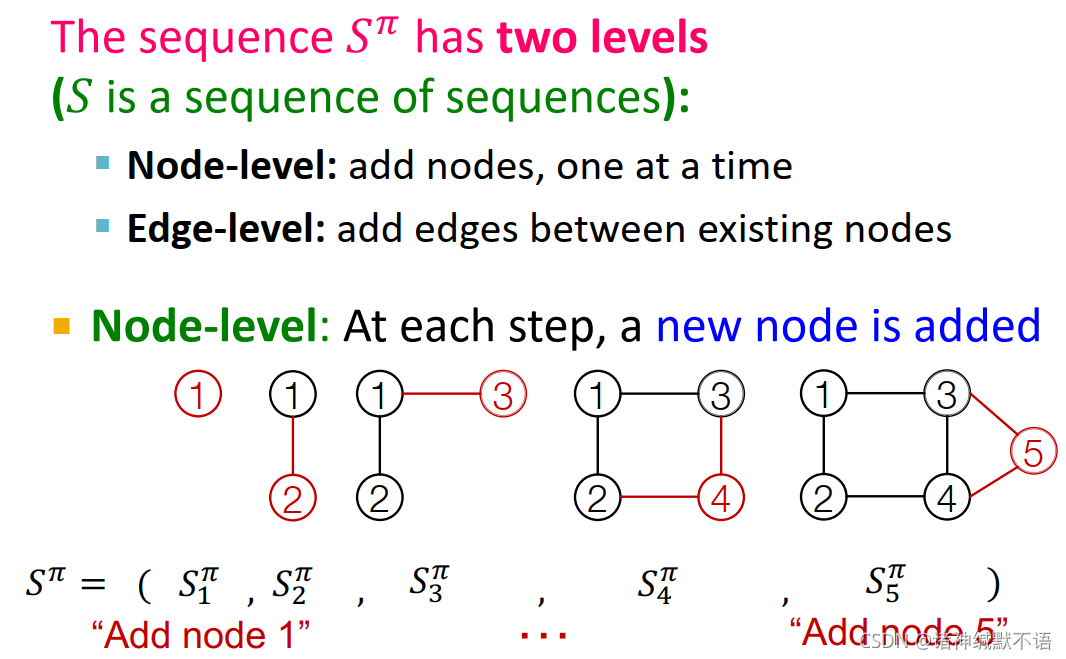
节点级别的每一步是一个边级别的序列:每一个元素是是否与该节点添加一条边,即形成一个如图所示的0-1变量序列:
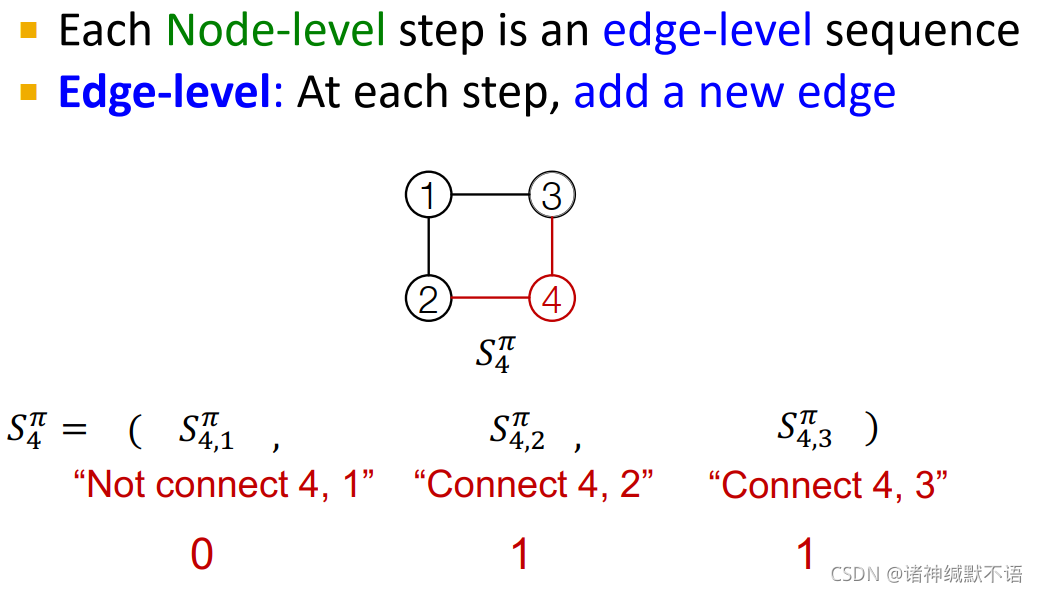
这里的node ordering是随机选的,随后我们会讨论这一问题。
如图所示,每一次是生成邻接矩阵(黄色部分)中的一个节点(向右),每个节点生成一列边(向下):
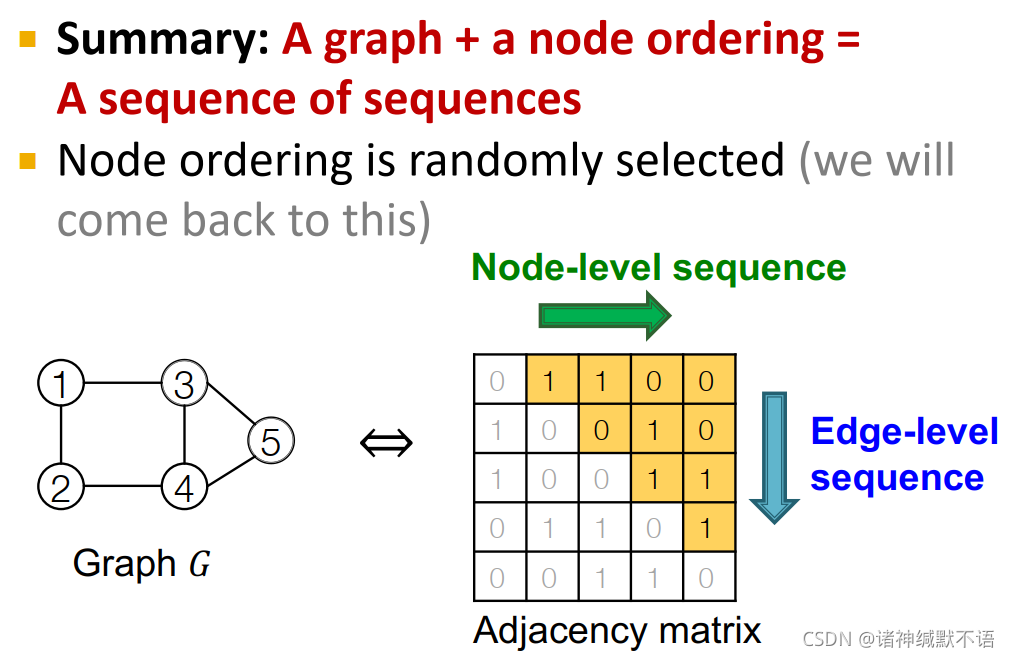
这样我们就将图生成问题转化为序列生成问题。
我们需要建模两个过程:
(1) 生成一个新节点的state(节点级别序列)
(2) 根据新节点state生成它与之前节点相连的边(边级别序列)
方法:用Recurrent Neural Networks (RNNs) 建模这些过程

-
RNN
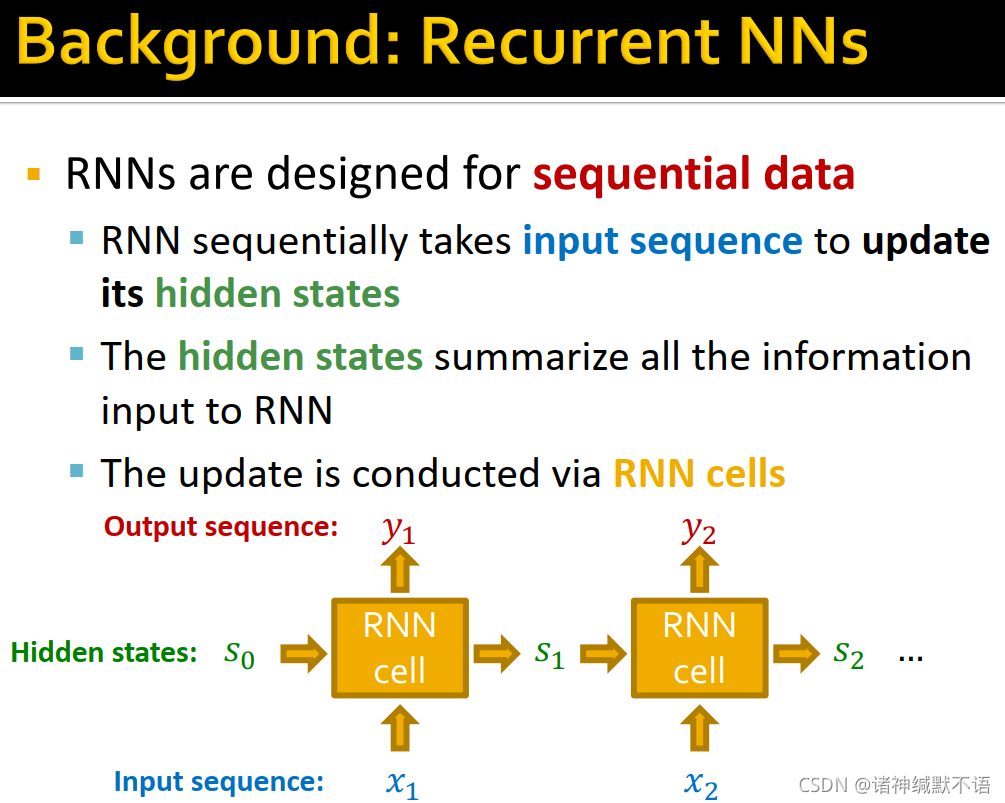
RNNs是为序列数据所设计的,它sequentially输入序列数据以更新其hidden states,其hidden states包含已输入RNN的所有信息。更新过程由RNN cells实现。
图示流程:
-
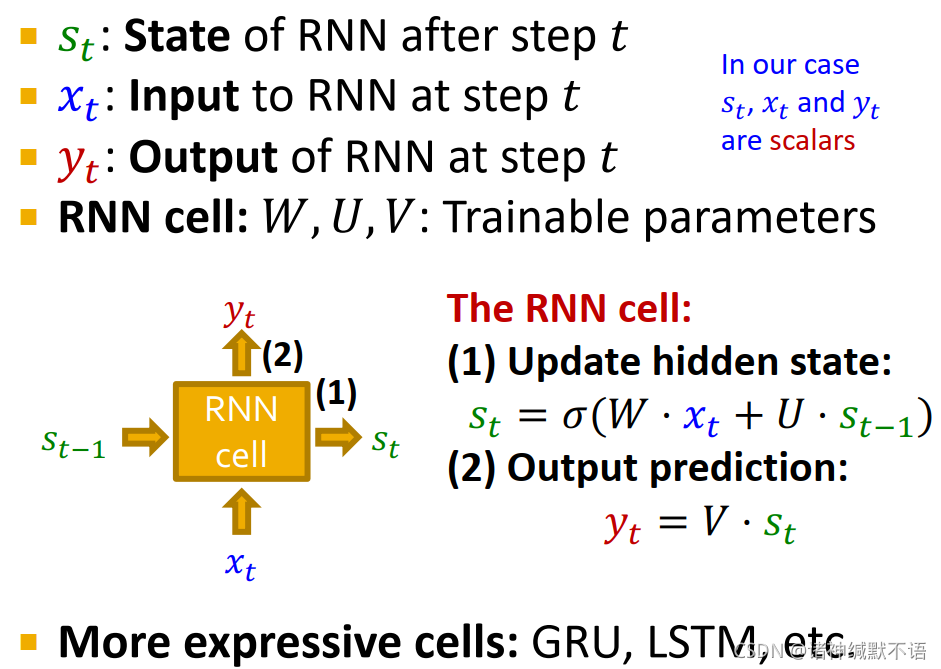
RNN cell
s t s_t st: RNN在第 t t t 步之后的state
x t x_t xt: RNN在第 t t t 步的输入
y t y_t yt: RNN在第 t t t 步的输出
(在我们的例子中,上述三个值都是标量)
RNN cell: 可训练参数 W , U , V W,U,V W,U,V
第一步:根据输入和上一步state更新hidden state: s t = σ ( W ⋅ x t + U ⋅ s t − 1 ) s_t=\sigma(W\cdot x_t+U\cdot s_{t-1}) st=σ(W⋅xt+U⋅st−1)
第二步:根据state进行输出: y t = V ⋅ s t y_t=V\cdot s_t yt=V⋅st
还有更具有表现力的cells:GRU,LSTM等
-
GraphRNN: Two levels of RNN
GraphRNN有一个节点级别RNN和一个边级别RNN,节点级别RNN生成边级别RNN的初始state,边级别RNN sequentially预测这个新节点与每一个之前的节点是否相连。

如图所示,边级别RNN预测新加入的节点是否与之前各点相连:
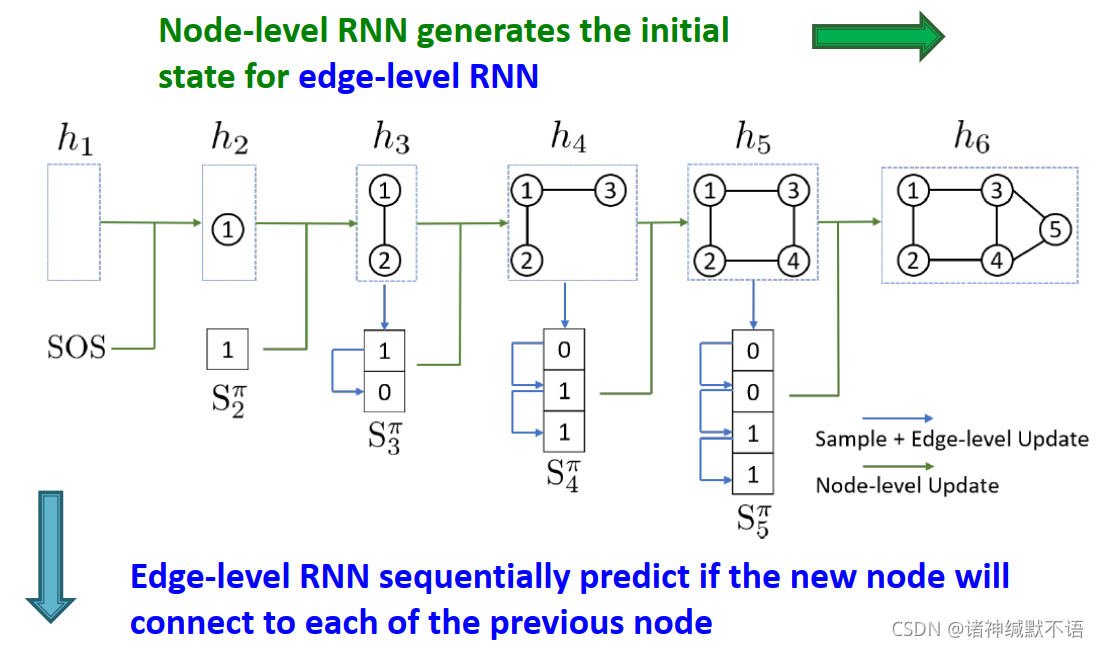
接下来将介绍如何用这个RNN生成序列。

-
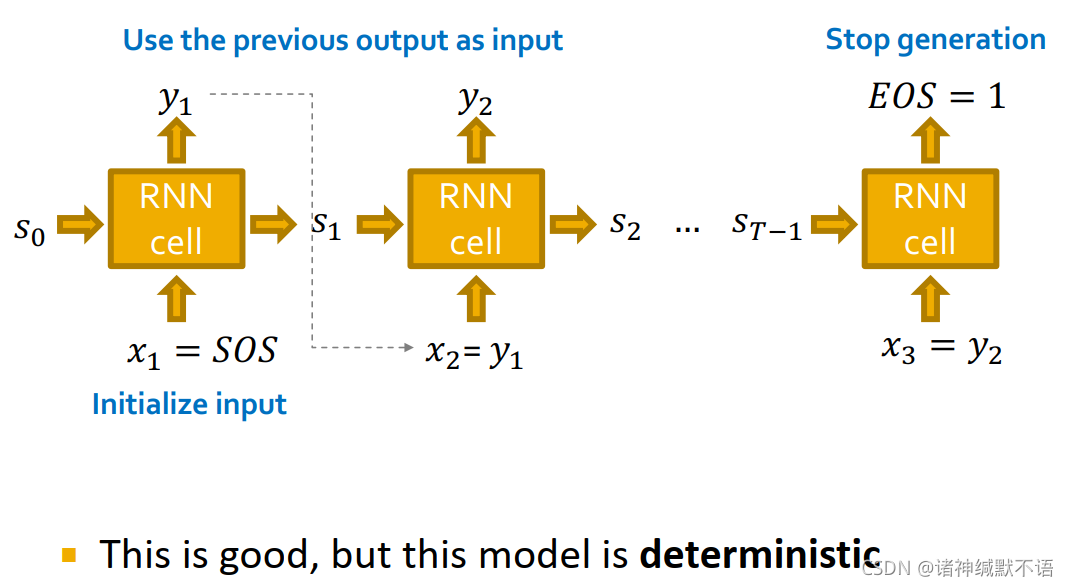
(1) 用RNN生成序列:用前一个cell的输出作为下一个cell的输入( x t + 1 = y t x_{t+1}=y_t xt+1=yt)。
(2) 初始化输入序列:用 start of sequence token (SOS) 作为初始输入。SOS常是一个全0或全1的向量。
(3) 结束生成任务:用 end of sequence token (EOS) 作为RNN额外输出。
如果输出EOS=0,则RNN继续生成;如果过输出EOS=1,则RNN停止生成。

模型如图所示:
这样的问题在于模型是确定的,但我们需要生成的是分布,所以需要模型具有随机性。
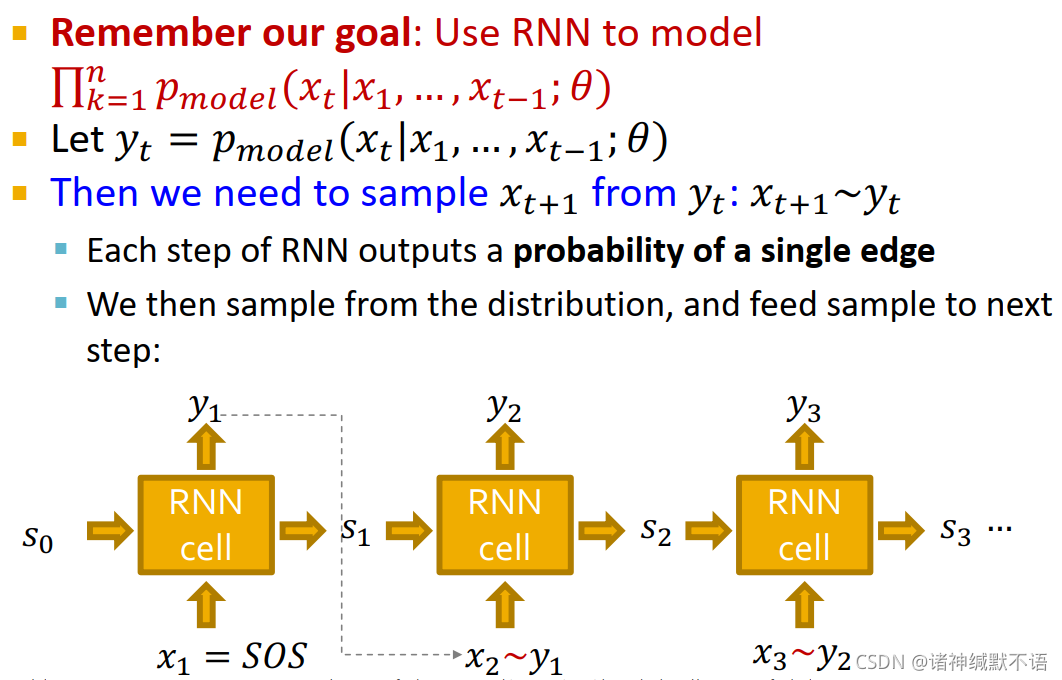
我们的目标就是用RNN建模 ∏ k = 1 n p m o d e l ( x t ∣ x 1 , … , x t − 1 ; θ ) \prod_{k=1}^np_{model}(x_t|x_1,\dots,x_{t-1};\theta) ∏k=1npmodel(xt∣x1,…,xt−1;θ)
所以我们让 y t = p m o d e l ( x t ∣ x 1 , … , x t − 1 ; θ ) y_t=p_{model}(x_t|x_1,\dots,x_{t-1};\theta) yt=pmodel(xt∣x1,…,xt−1;θ),然后从 y t y_t yt 中抽样 x t + 1 x_{t+1} xt+1,即 x t + 1 ∼ y t x_{t+1}\sim y_t xt+1∼yt:
RNN每一步产生一条边的生成概率,我们依此抽样并将抽样结果输入下一步。
如图所示:
-
RNN at Test Time
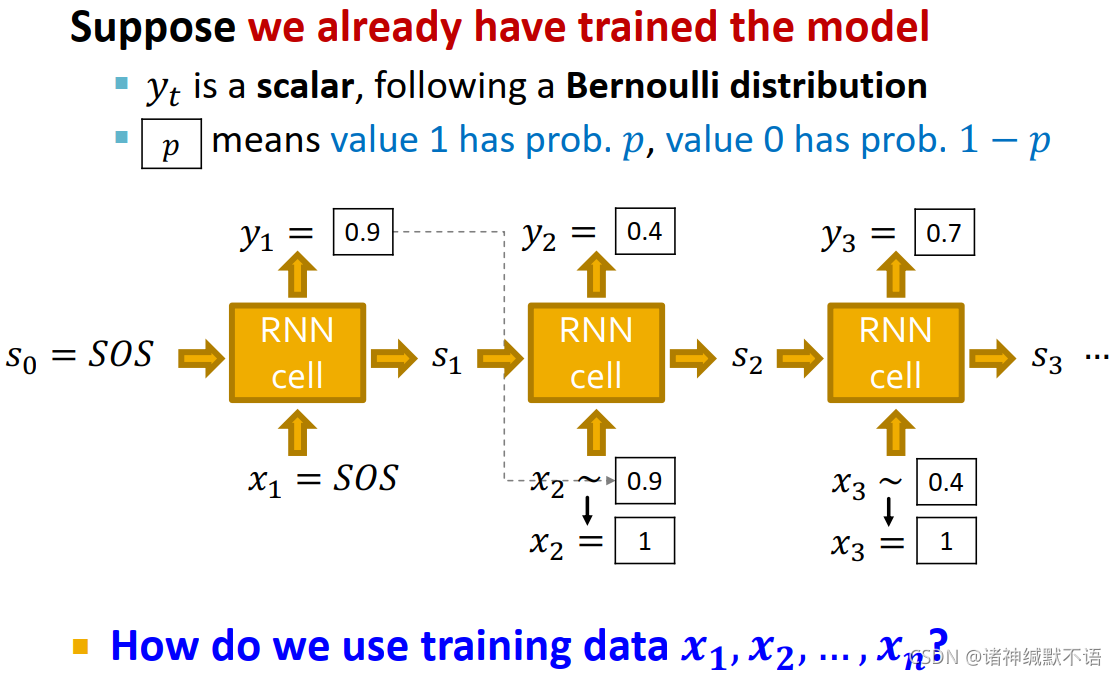
我们假设已经训练好了模型:
y t y_t yt 是 x t + 1 x_{t+1} xt+1 是否为1这一遵从伯努利分布事件的概率,从而根据模型我们可以从输入输出 y t y_{t} yt,从而抽样出 x t + 1 x_{t+1} xt+1。
如图所示:
-
RNN at Training Time
在训练过程中,我们已知的数据就是序列 y ∗ y^* y∗(该节点与之前每一节点是否相连的0-1元素组成的序列)。
我们使用teacher forcing7 的方法,将每一个输入都从前一个节点的输出换成真实序列值,而用真实序列值与模型输出值来计算损失函数。如图所示:
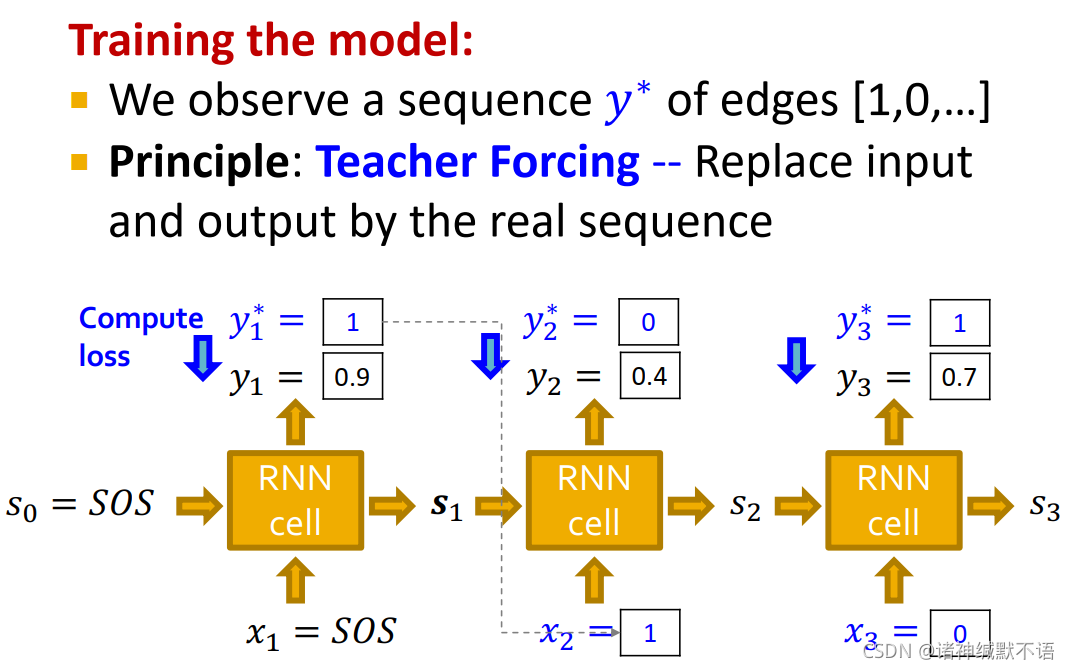
这一问题的损失函数使用binary cross entropy8,即最小化下式损失函数:
L = − [ y 1 ∗ log ( y 1 ) + ( 1 − y 1 ∗ ) log ( 1 − y 1 ) ] L=-\big[y_1^*\log(y_1)+(1-y_1^*)\log(1-y_1)\big] L=−[y1∗log(y1)+(1−y1∗)log(1−y1)]
对每一个输出,上式右式左右两项同时只能存在一个:
如果边存在,即 y 1 ∗ = 1 y_1^*=1 y1∗=1,则我们需要最小化 − log ( y 1 ) -\log(y_1) −log(y1),即使 y 1 y_1 y1 增大 因为 log \log log 递增,所以 − log -\log −log 递减
如果边不存在,即 y 1 ∗ = 0 y_1^*=0 y1∗=0,我们需要最小化 − log ( 1 − y 1 ) -\log(1-y_1) −log(1−y1),即使 y 1 y_1 y1 减小 因为 log \log log 递增, 1 − x 1-x 1−x 递减,所以 log ( 1 − x ) \log(1-x) log(1−x) 递减,所以 − log ( 1 − x ) -\log(1-x) −log(1−x) 递增
这样就使 y 1 y_1 y1 靠近data samples y 1 ∗ y_1^* y1∗
y 1 y_1 y1 是由RNN计算得到的,通过这一损失函数,使用反向传播就能对应调整RNN参数。

-
Putting Things Together
我们的计划是:- 增加一个新节点:跑节点RNN,用其每一步输出来初始化边RNN
- 为新节点增加新边:跑边RNN,预测新节点是否与每一之前节点相连
- 增加另一个新节点:用边RNN最后的hidden state来跑下一步的节点RNN
- 停止图生成任务:如果边RNN在第一步输出EOS,则我们知道新节点上没有任何一条边,即不再与之前的图有连接,从而停止图生成过程。

-
训练过程
假设节点1已在图中,现在添加节点2:输入SOS到节点RNN中
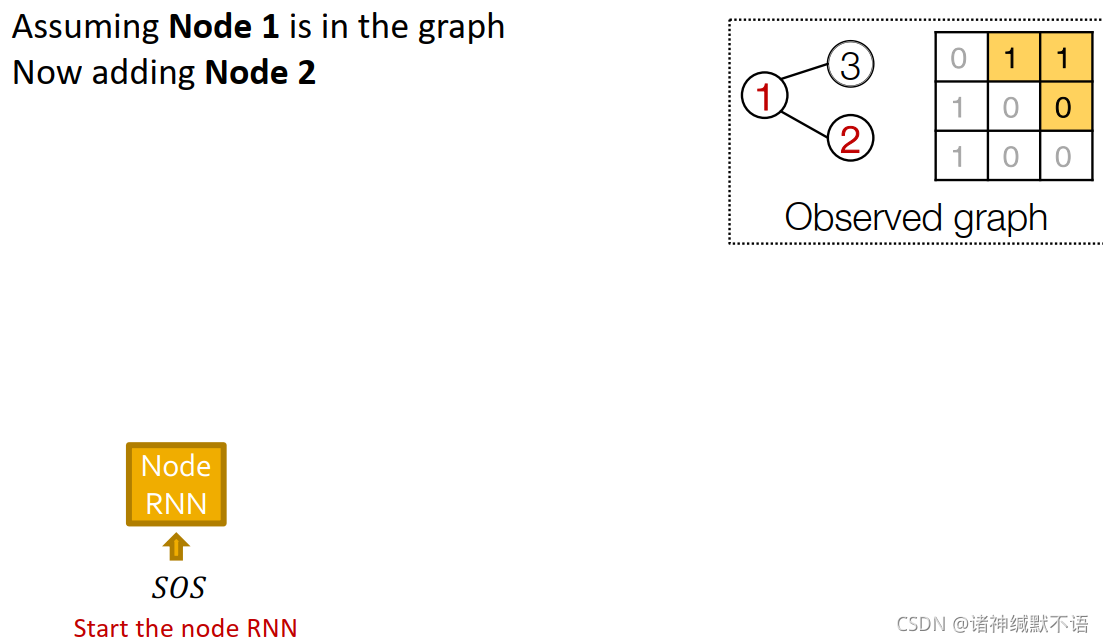
边RNN预测节点2是否会与节点1相连:输入SOS到边RNN中,输出节点2是否会与节点1相连的概率0.5
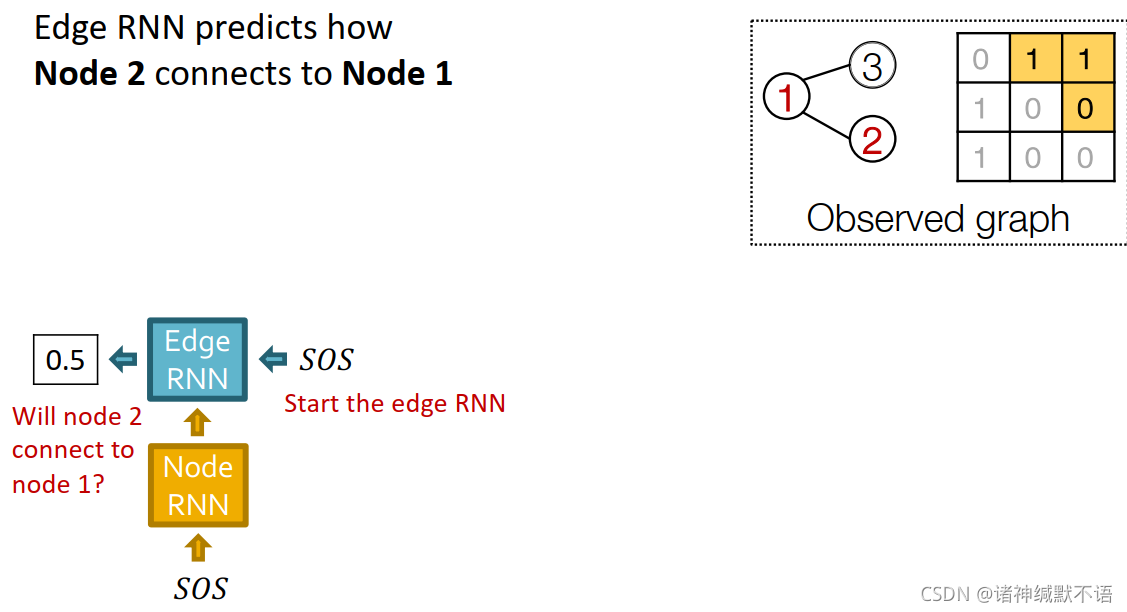
用边RNN的hidden state更新节点RNN:
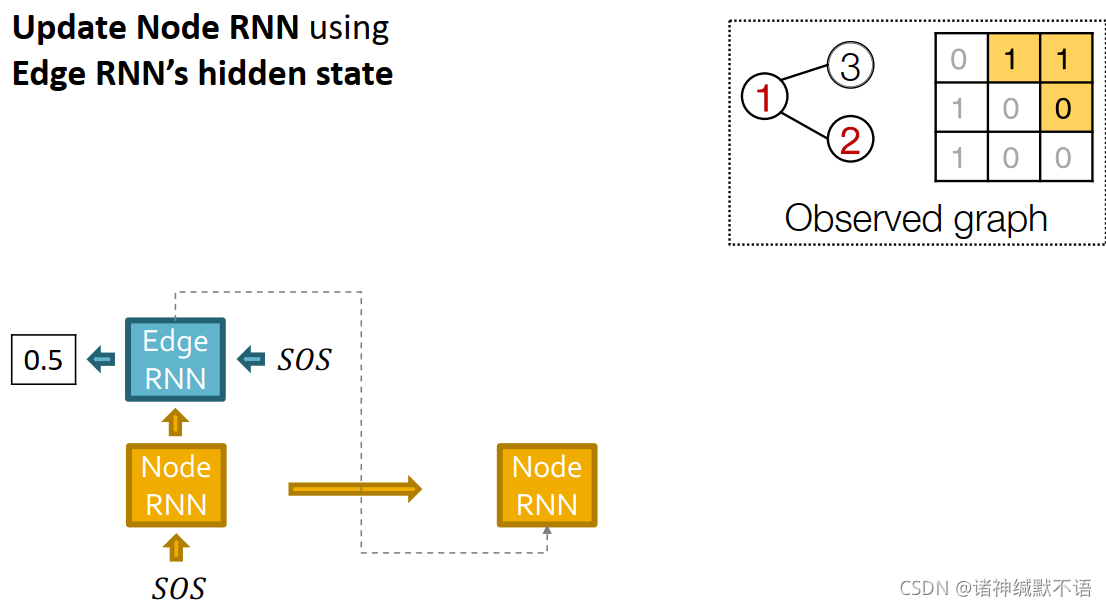
边RNN预测节点3是否会与节点1、2相连:输入SOS到边RNN中,输出节点3是否会与节点2相连的概率0.6;输入节点3与节点2不相连的真实值0到下一个cell中,输出节点3是否会与节点2相连的概率0.4:
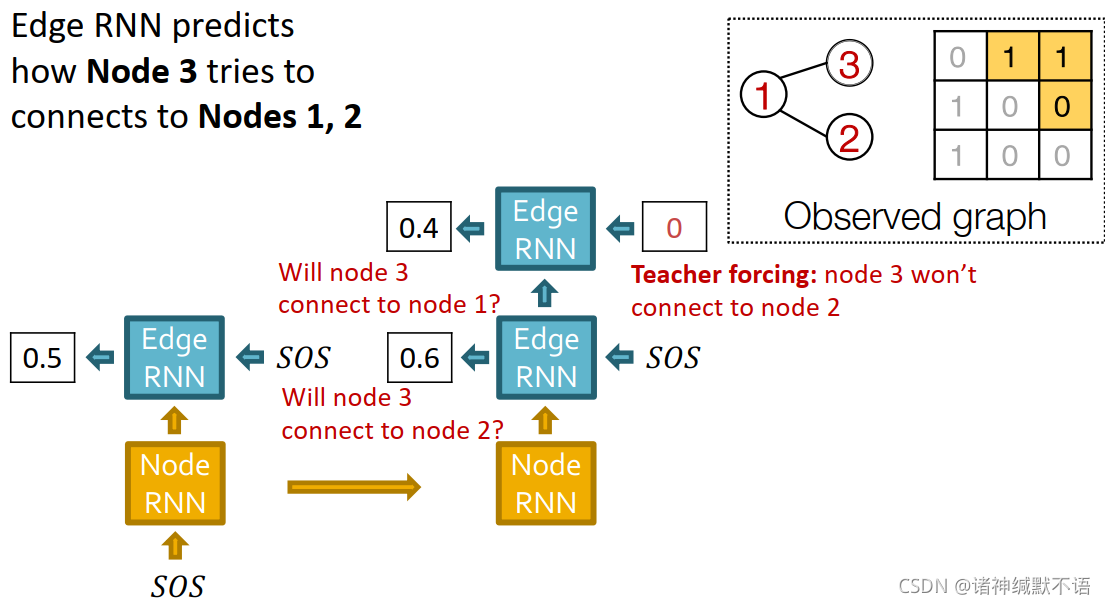
用边RNN的hidden state更新节点RNN:
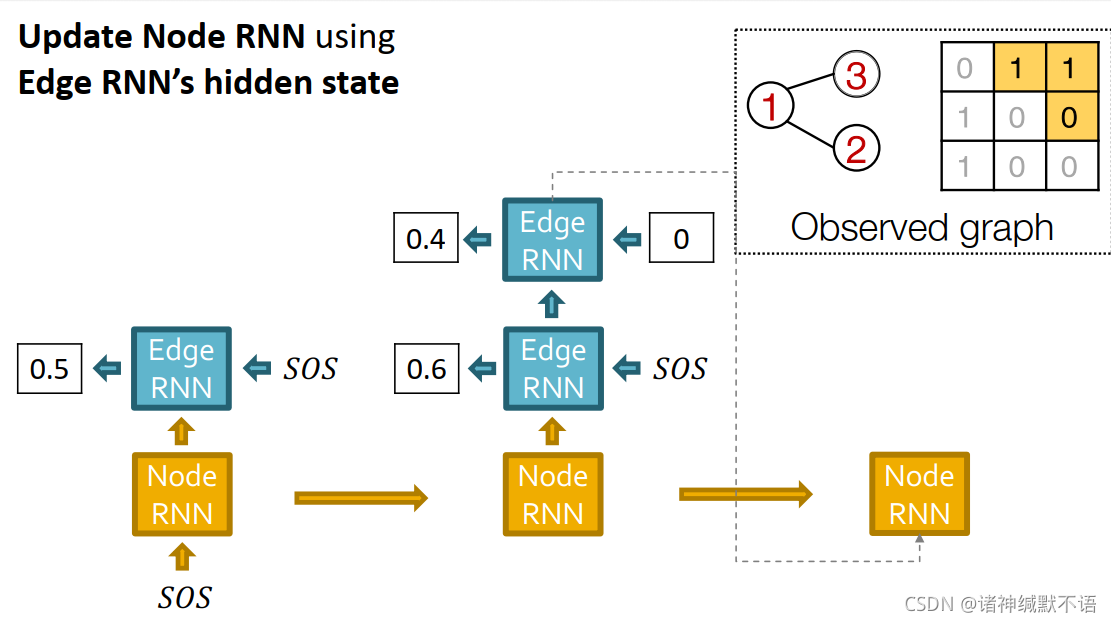
我们已知节点4不与任何之前节点相连,所以停止生成任务:输入SOS到边RNN中,没看懂这里是不是用teacher forcing强制停止的意思。
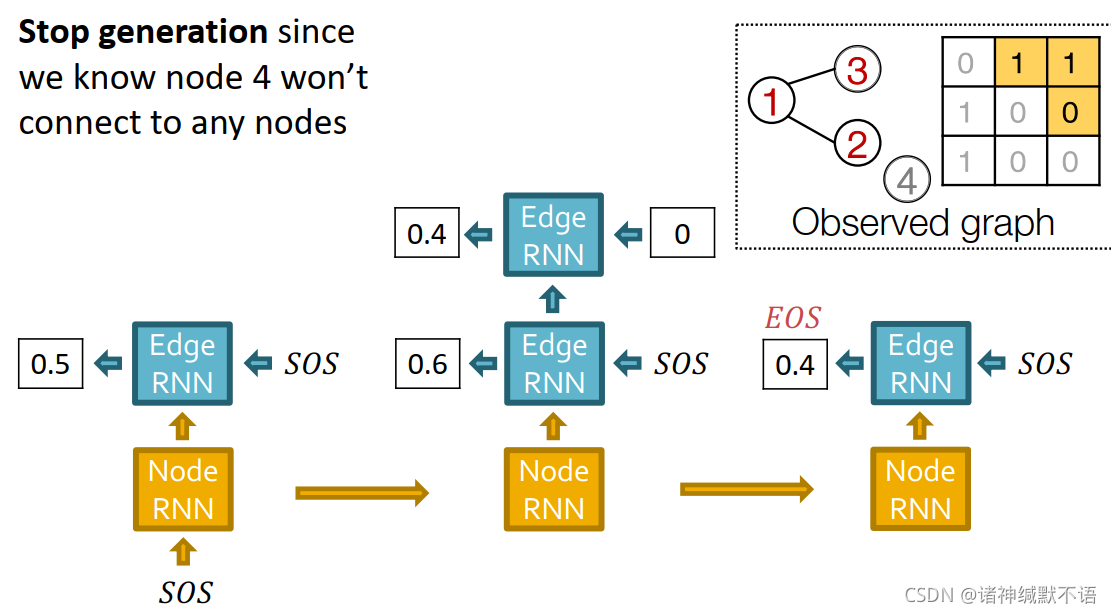
每一步我们都用真实值作为监督,如图所示,就跟右上角的图形式或邻接矩阵形式一样的真实值:
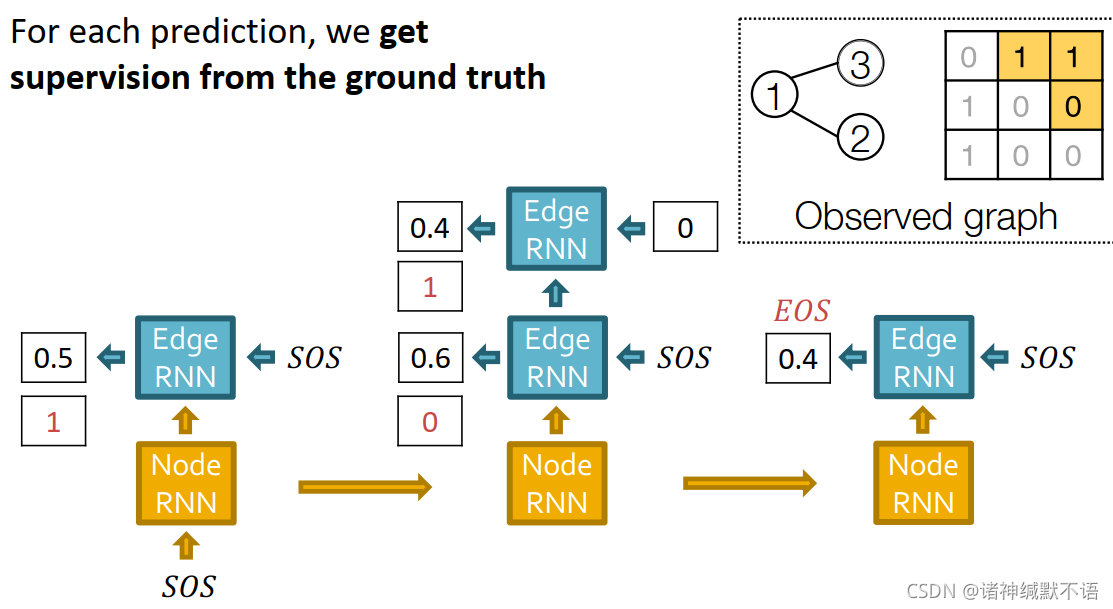
通过时间反向传播,随time step9 累积梯度,如图所示:
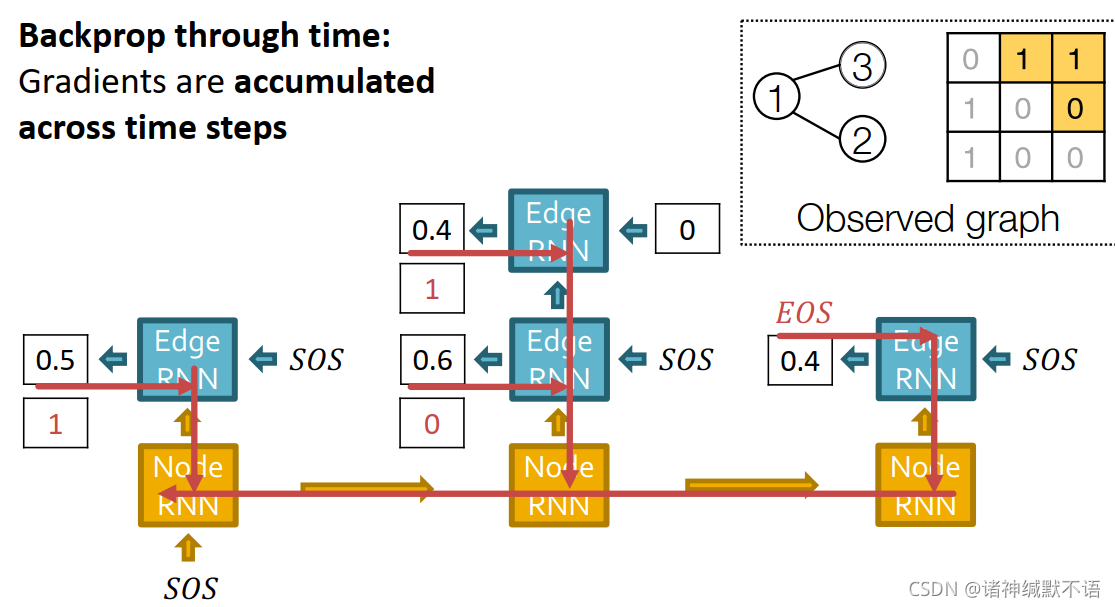
-
测试阶段
- 根据预测出来的边分布抽样边
- 用GraphRNN自己的预测来代替每一步输入(就类似训练阶段如果不用tearcher forcing的那种效果)
如图所示:
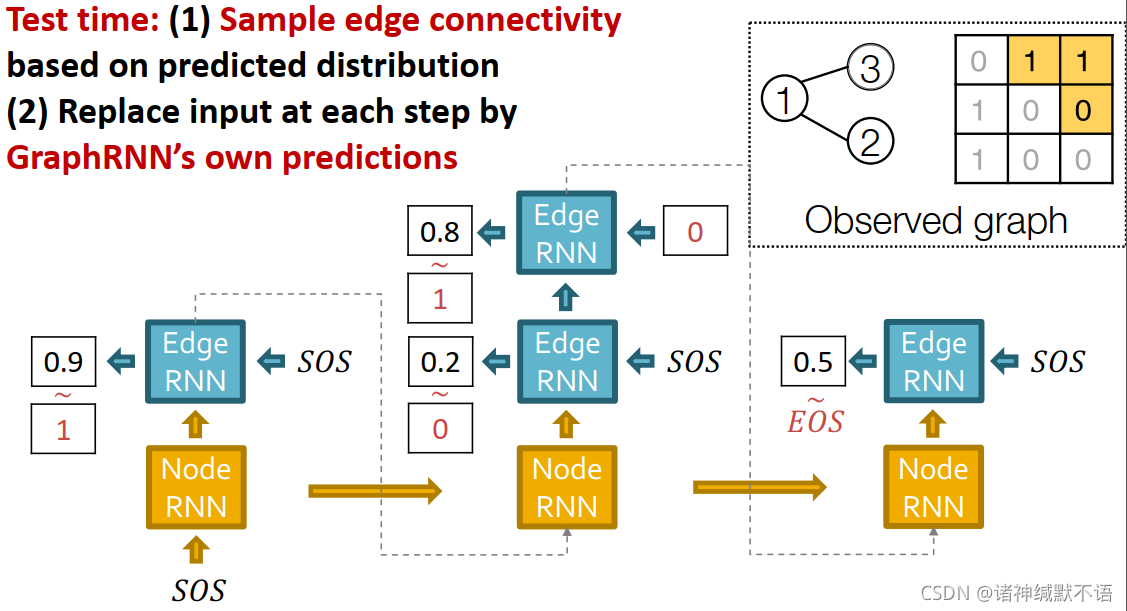
-
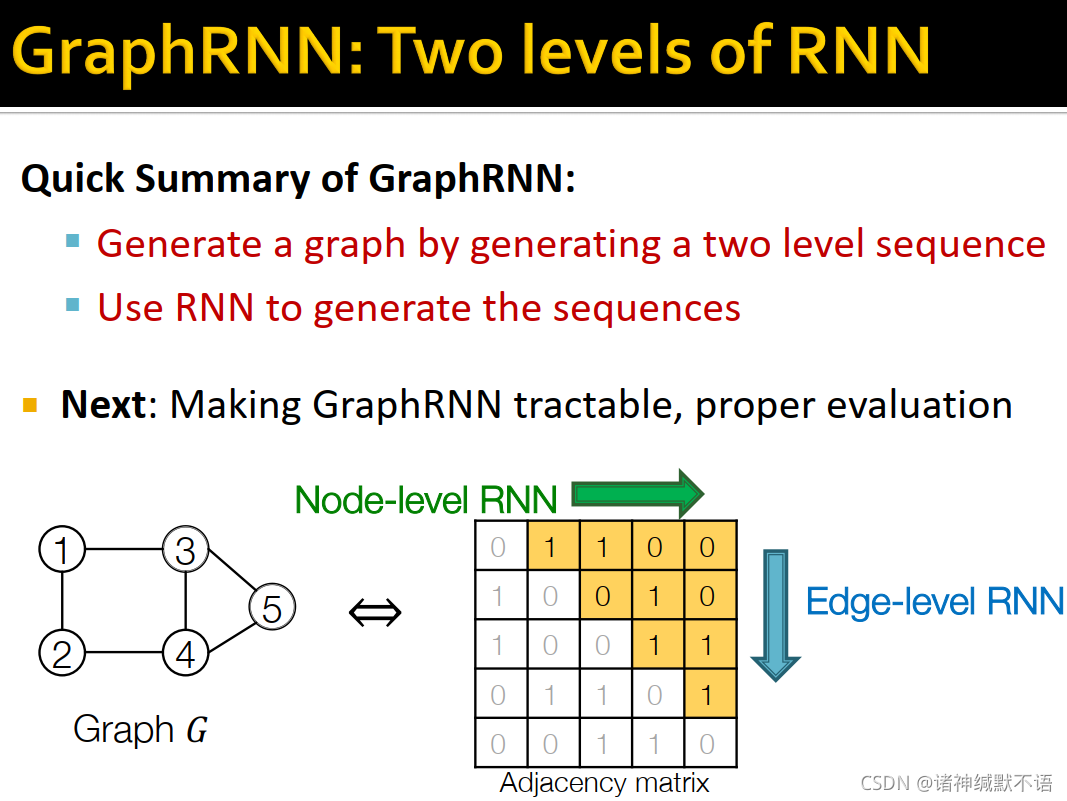
GraphRNN总结:
通过生成一个2级序列来生成一张图,用RNN来生成序列。如图中所示,节点级别RNN向右预测,边级别RNN向下预测。
接下来我们要使RNN tractable,以及对其效果进行评估。
-
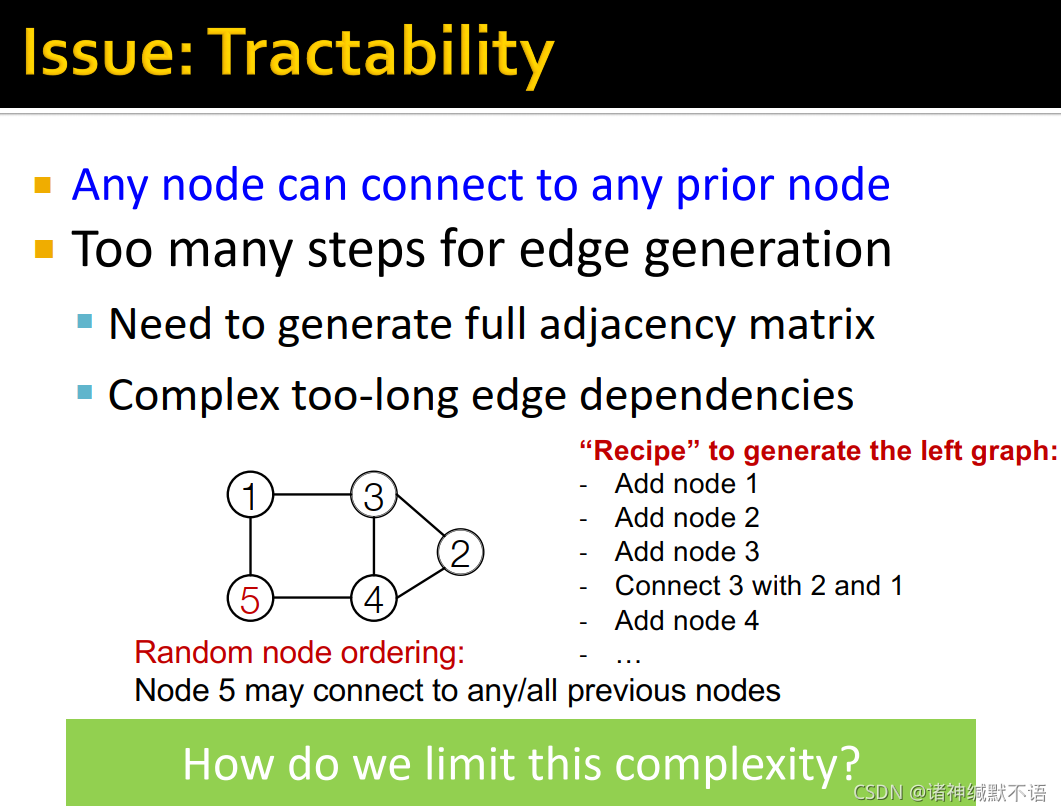
tractability
在此前的模型中,每一个新节点都可以与其前任何一个节点相连,这需要太多步边生成了,需要产生一整个邻接矩阵(如上图所示),也有太多过长的边依赖了(不管已经有了多少个节点,新节点还要考虑是否与最前面的几个节点有边连接关系)。
如果我们使用随机的node ordering,那我们对每个新生成的节点就是都要考虑它与之前每一个节点是否有边(图中左下角所示):
-
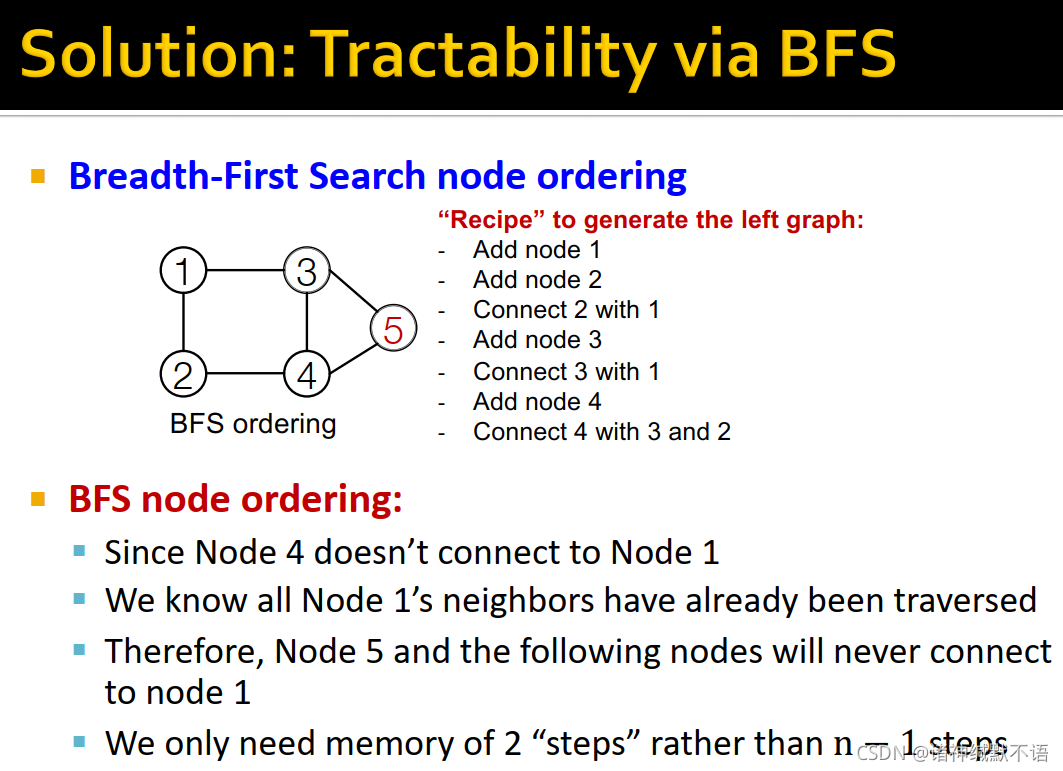
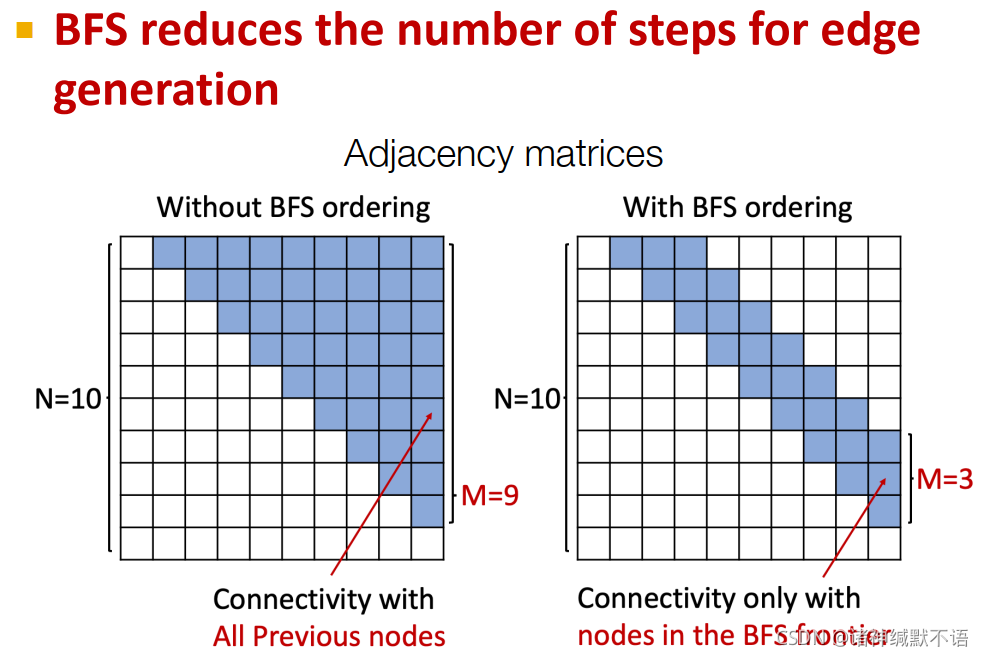
BFS
但是如果我们换成一种BFS的node ordering,那么在对每个边考虑它可能相连的之前节点的过程如图所示,我们只需要考虑在BFS时它同层和上一层的节点(因为再之前的节点跟它不会有邻居关系),即只需要考虑2步的节点而非 n − 1 n-1 n−1 步的节点:
这样的好处有二:
(1) 减少了可能存在的node ordering数量(从 O ( n ! ) O(n!) O(n!) 减小到不同BFS ordering的数量)
(2) 减少了边生成的步数(因为不需要看之前所有节点了,只需要看一部分最近的节点即可)
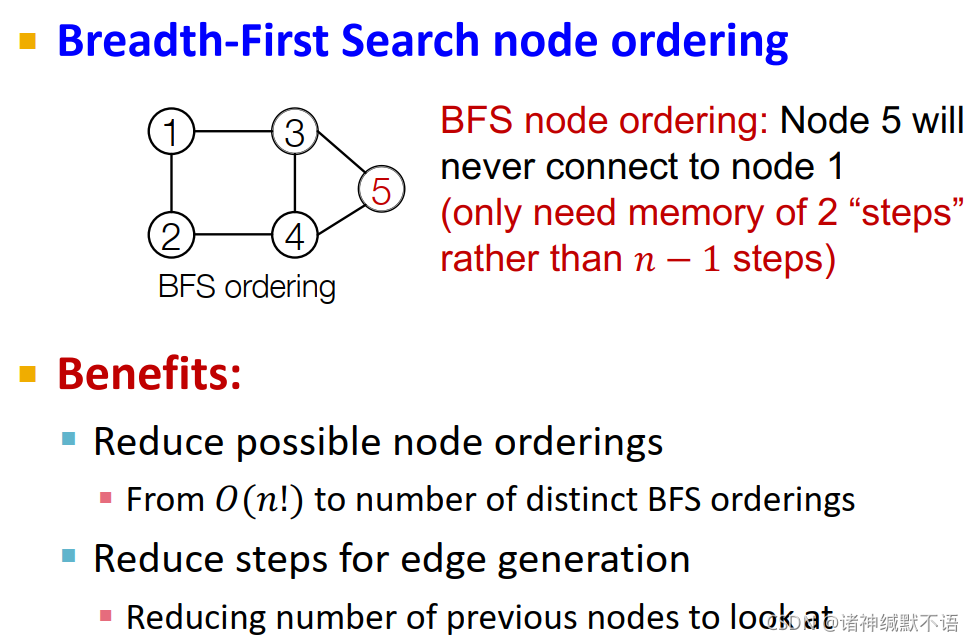
在运行GraphRNN时仅需考虑该节点及其之前的一部分节点,如图所示10:
-
对生成图的评估
我们的数据集是若干图,输出也是若干图,我们要求评估这两组图之间的相似性。有直接从视觉上观察其相似性和通过图统计指标来衡量其相似性两种衡量方式。
- visual similarity
就直接看,能明显地发现在grid形式的图上,GraphRNN跟输入数据比传统图生成模型(主要用于生成网络而非这种grid图)要更像很多:
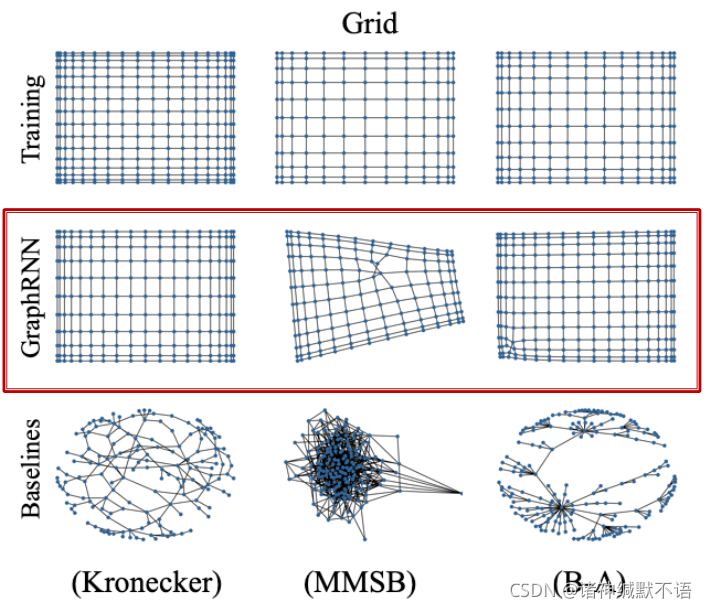
(图中Kronecker就是上节课讲的那个模型。其他baseline模型具体哪个对应哪个可以在 1这篇论文中找。这个图就是原论文中的插图)
即使在传统图生成模型应用的有社区的社交网络上,GraphRNN也表现很好,如图所示。这体现了GraphRNN的可泛化能力。
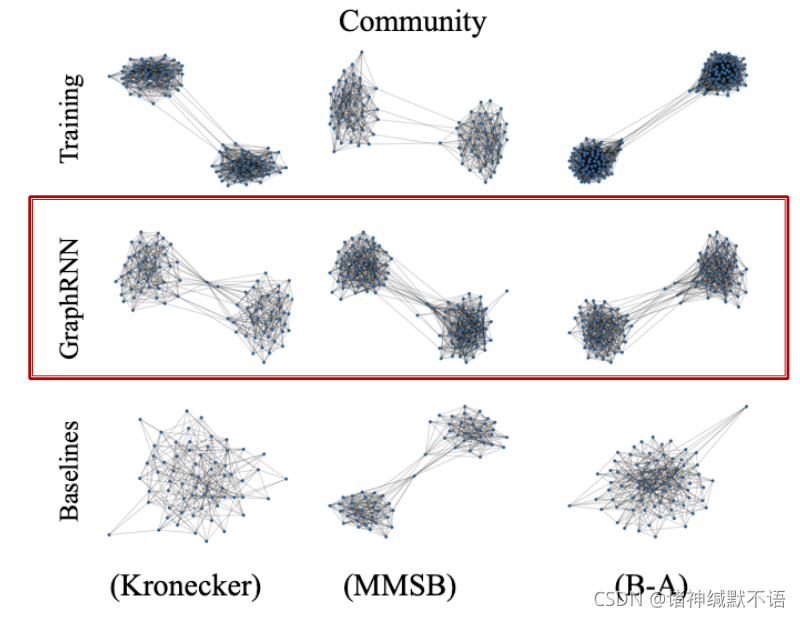
- graph statistics similarity
我们想找到一些比目测更精确的比较方式,但直接在两张图的结构之间作比较很难(同构性检测是NP的),因此我们选择比较图统计指标。
典型的图统计指标包括:
(1) degree distribution (Deg.)
(2) clustering coefficient distribution (Clus.)
(3) orbit count statistics 11
注意:每个图统计指标都是一个概率分布。

所以我们一要比较两种图统计指标(两个概率分布),解决方法是earth mover distance (EMD);二要比较两个图统计指标的集合(两个概率分布的集合),解决方法是基于EMD的maximum mean discrepancy (MMD)。
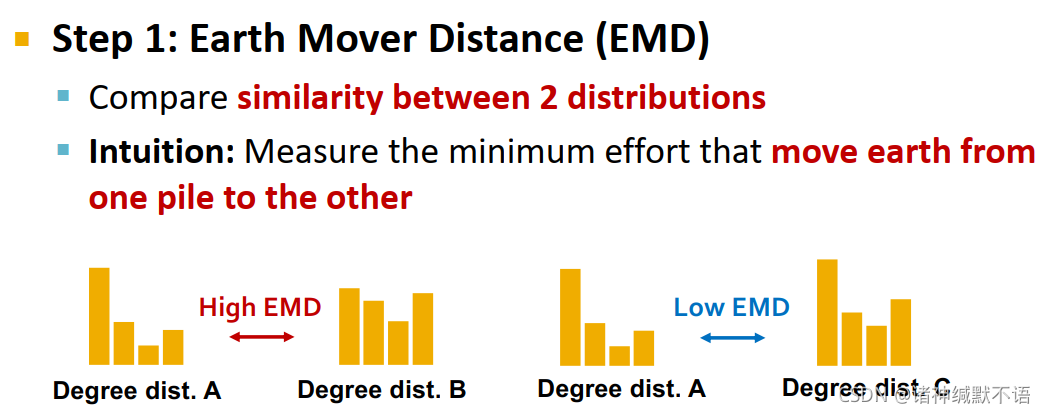
- earth mover distance (EMD)
用于比较两个分布之间的相似性。在直觉上就是衡量需要将一种分布编程另一种分布所需要移动的最小“泥土量”(面积)。总之这里有个公式,但是我也没仔细看具体怎么搞的。或许可以参考一下EMD的英文维基百科Earth mover’s distance - Wikipedia,以后有缘可以学习:

- maximum mean discrepancy (MMD)
基于元素相似性,比较集合相似性:使用L2距离,对每个元素用EMD计算距离,然后用L2距离计算MMD。
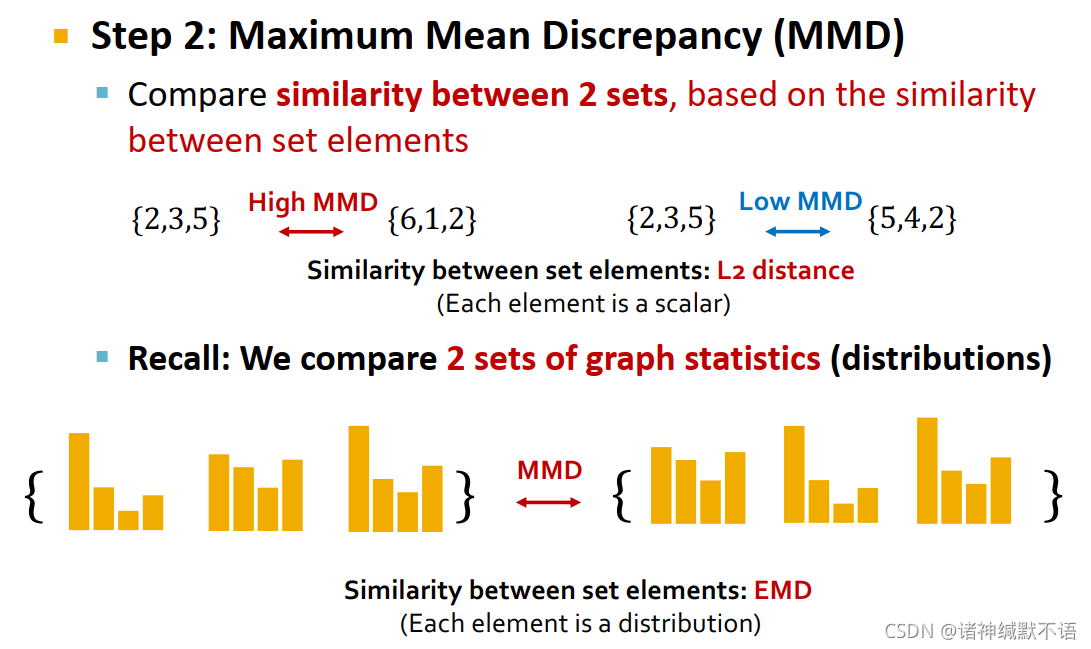
呃但是这个公式我委实是没有看懂:
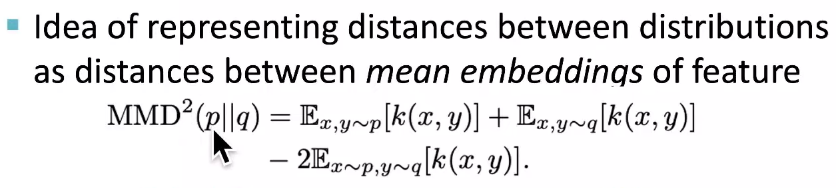
……什么东西啊这是?
- earth mover distance (EMD)
- 对图生成结果的评估:
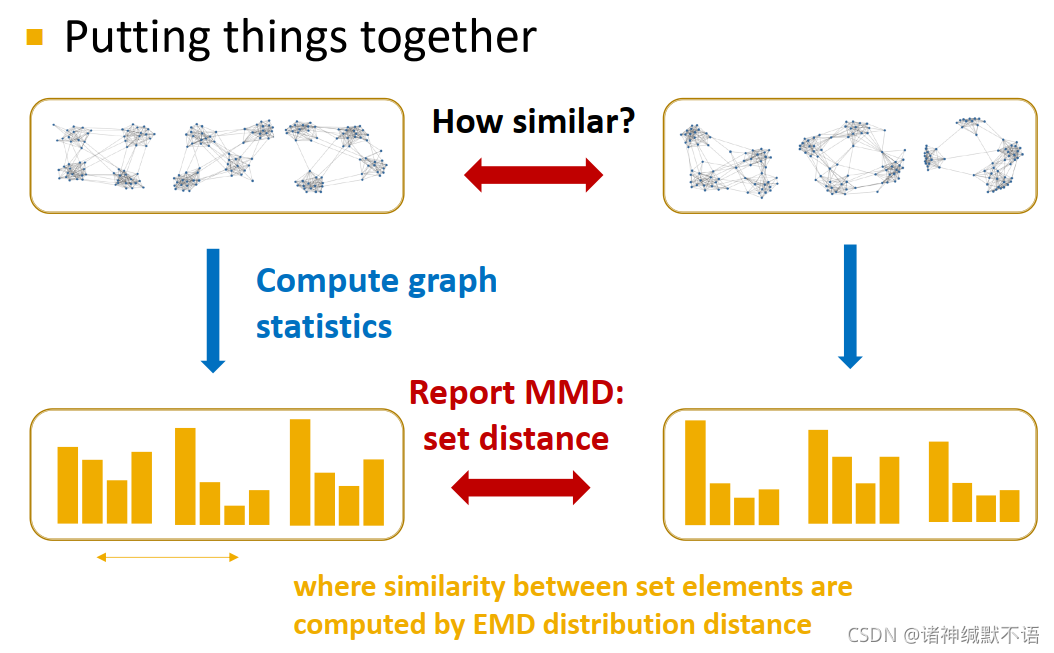
计算举例:通过计算原图域生成图之前在clustering coefficient distribution上的区别,我们发现GraphRNN是表现最好的(即最相似的)。
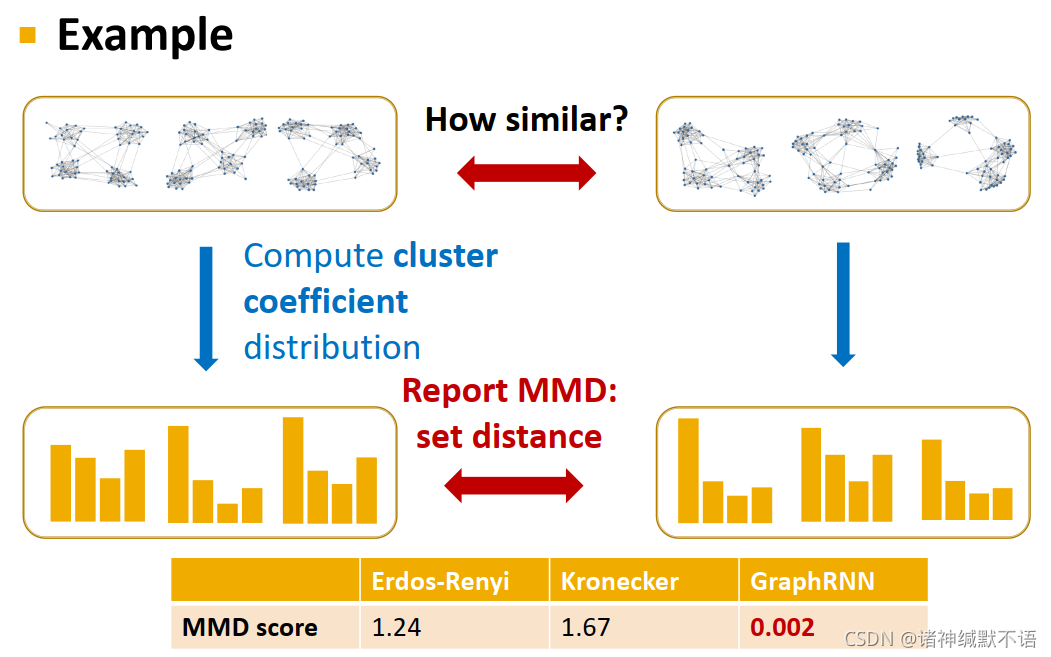
- visual similarity
4. Application of Deep Graph Generative Models
本节主要介绍深度图生成模型在药物发现领域的应用GCPN2。
- 药物发现领域的问题是:我们如何学习一个模型,使其生成valid、真实的分子,且具有优化过的某一属性得分(如drug-likeness或可溶性等)?
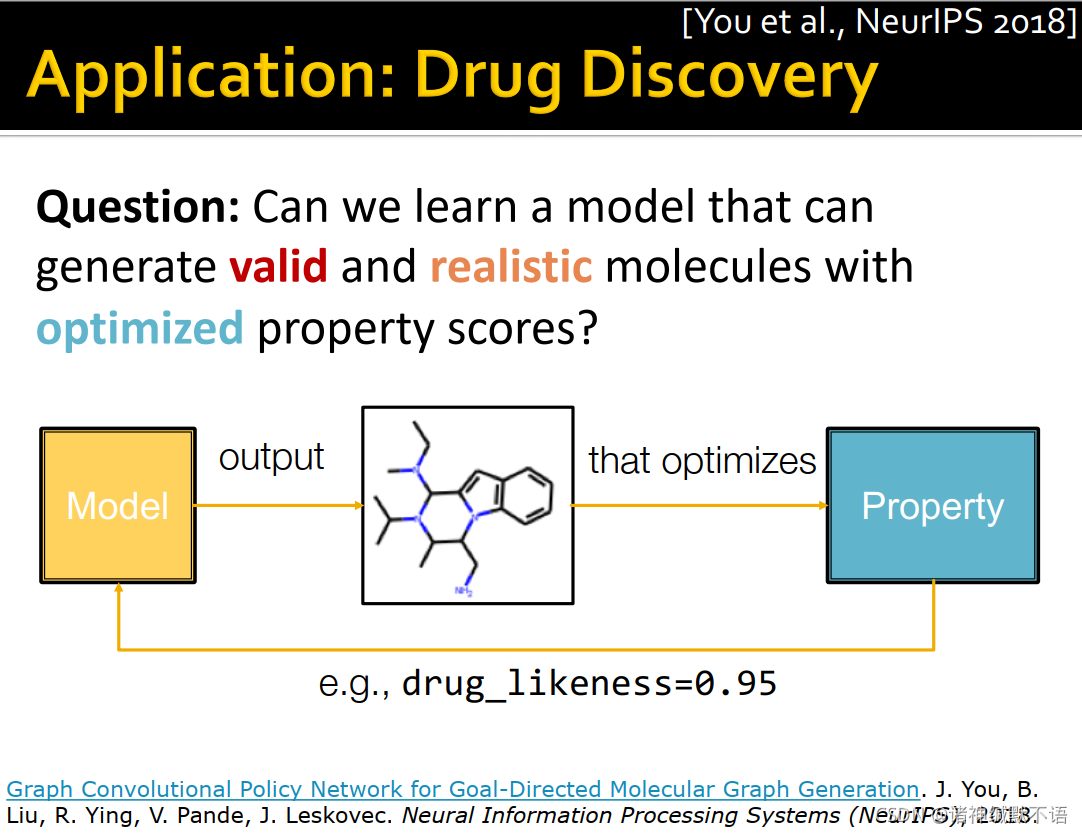
- 这种生成任务就是goal-directed graph generation:
① 优化一个特定目标得分(high scores),如drug-likeness
② 遵从内蕴规则(valid),如chemical validity rules
③ 从示例中学习(realistic),如模仿一个分子图数据集

- 这一任务的难点在于需要在机器学习中引入黑盒:像drug-likeness这种受物理定律决定的目标是我们不可知的。12

- 我们的解决思路是使用强化学习的思想
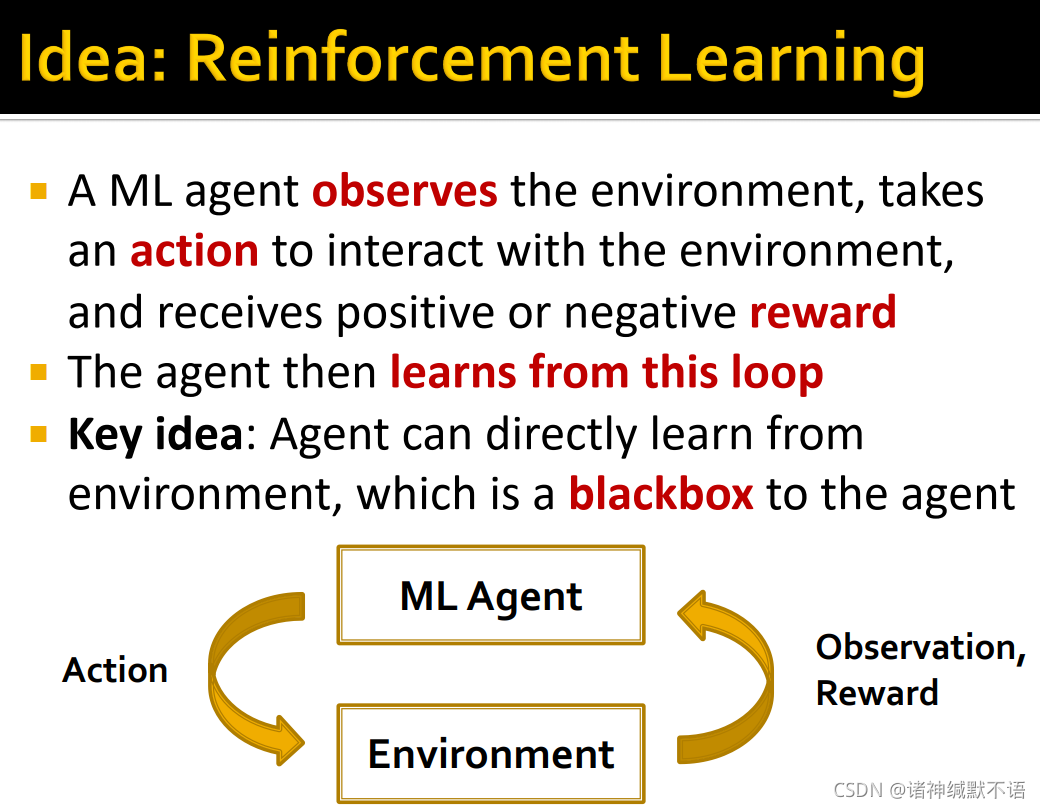
强化学习是一个机器学习agent观察环境environment,采取行动action来与环境互动interact,收到正向或负面的反馈reward,根据反馈从这一回环之中进行学习。回环如图所示。
其核心思想在于agent是直接从环境这一对agent的黑盒中进行学习的。
- 我们的解决方法是GCPN:graph convolutional policy network
结合了图表示学习和强化学习
核心思想:- GNN捕获图结构信息
- 强化学习指导导向预期目标的图生成过程
- 有监督训练模拟给定数据集的样例

- GCPN vs GraphRNN
- 共同点:
sequentially生成图
模仿给定的图数据集 - 主要差异:
- GCPN用GNN来预测图生成行为
优势:GNN比RNN更具有表现力
劣势:GNN比RNN更耗时(但是分子一般都是小图,所以我们负担得起这个时间代价) - GCPN使用RL来直接生成符合我们目标的图。RL使goal-directed graph generation成为可能。

- GCPN用GNN来预测图生成行为
- 共同点:
- sequential graph generation
GraphRNN:基于RNN hidden states(捕获至此已生成图部分的信息)预测图生成行为。
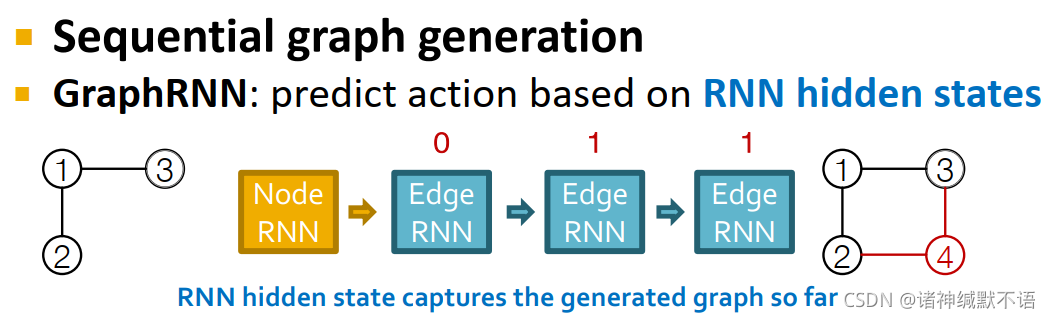
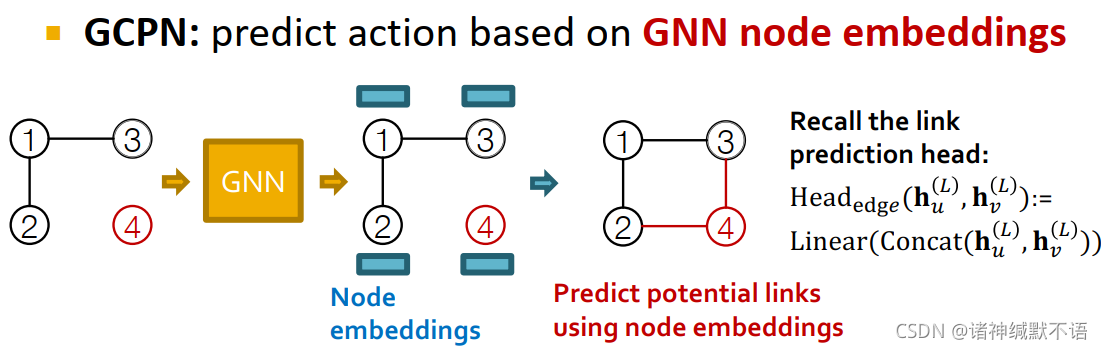
GCPN:基于GNN节点嵌入,用链接预测任务来预测图生成行为。
这种方式更具有表现力、更有鲁棒性,但更不scalable。
回忆链接预测任务的prediction head13,concatenation+linear这种方式就是: Head edge ( h u ( L ) , h v ( L ) ) = Linear ( Concat ( h u ( L ) , h v ( L ) ) ) \text{Head}_\text{{edge}}(\mathbf{h}_u^{(L)},\mathbf{h}_v^{(L)})=\text{Linear}\big(\text{Concat}(\mathbf{h}_u^{(L)},\mathbf{h}_v^{(L)})\big) Headedge(hu(L),hv(L))=Linear(Concat(hu(L),hv(L)))
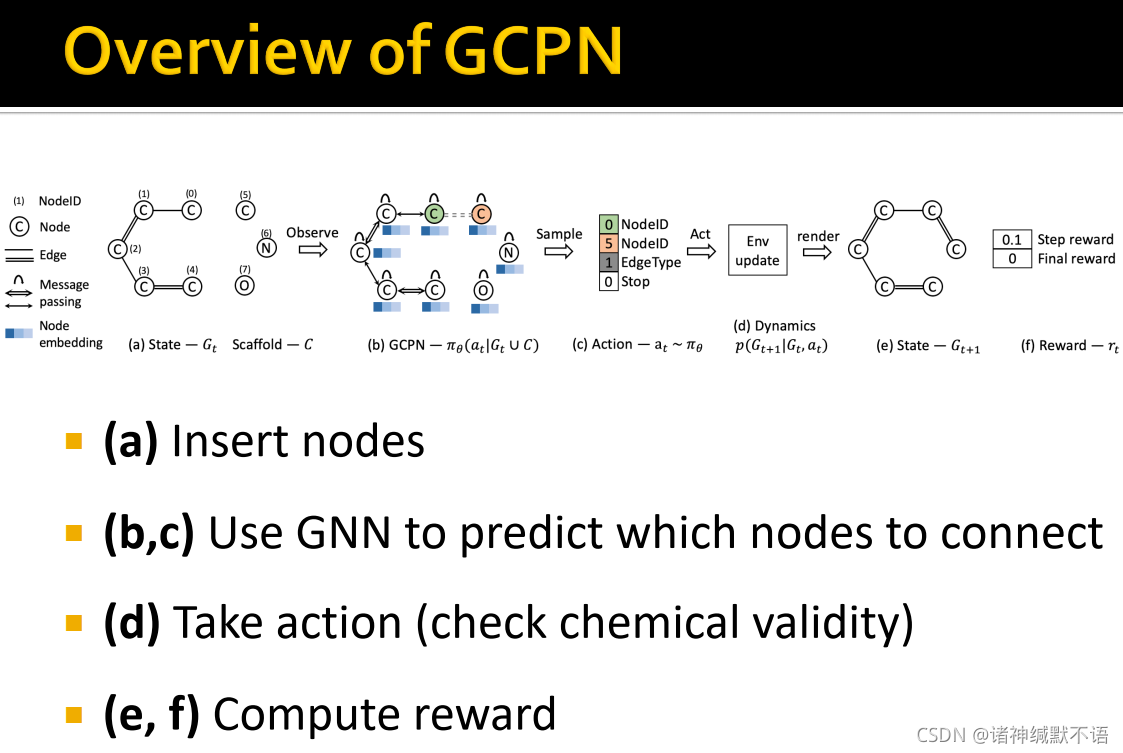
- GCPN概览
如图所示,首先插入节点5,然后用GNN预测节点5会与哪些节点相连,抽样边(action),检验其化学validity,计算reward。这个具体流程其实我也妹搞明白,强化学习这部分我就不太懂。以后有缘再仔细研究。
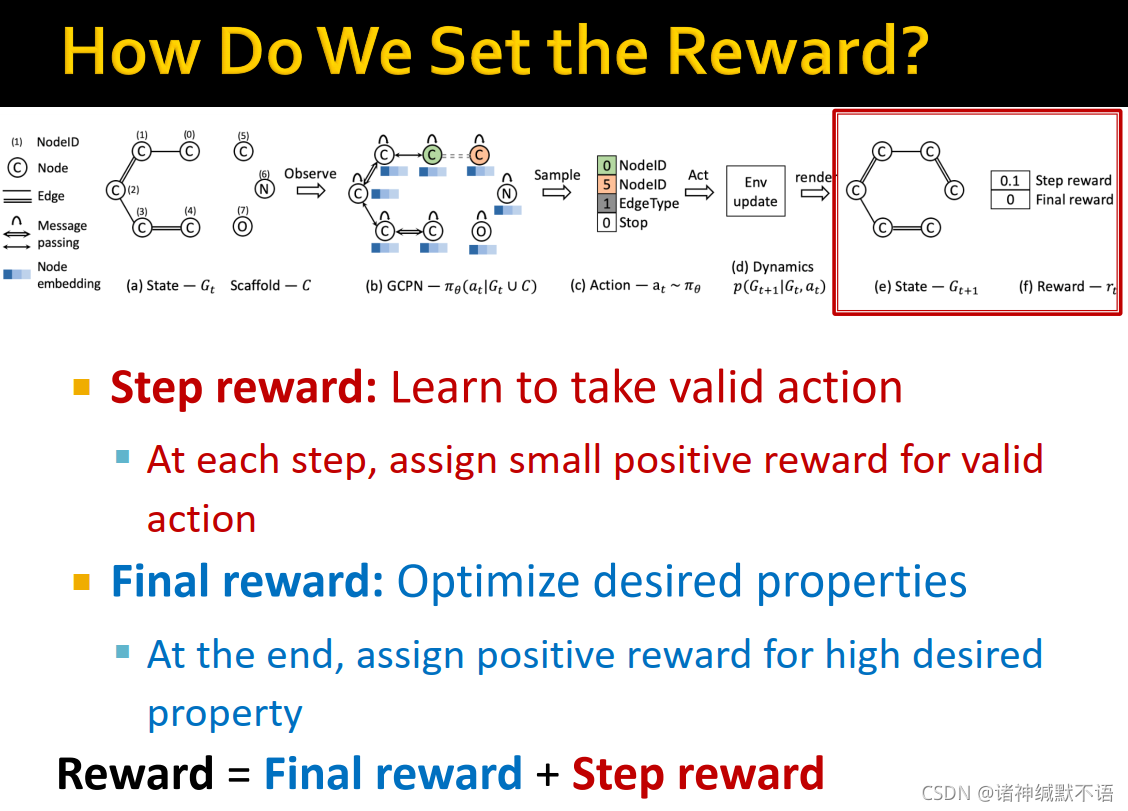
- 我们如何设置reward?
我们设置两种reward:
一种是step reward,学习执行valid action:每一步对valid action分配小的正反馈。
一种是final reward,优化预期属性:在最后对高预期属性分配正反馈。
reward=final reward + step reward
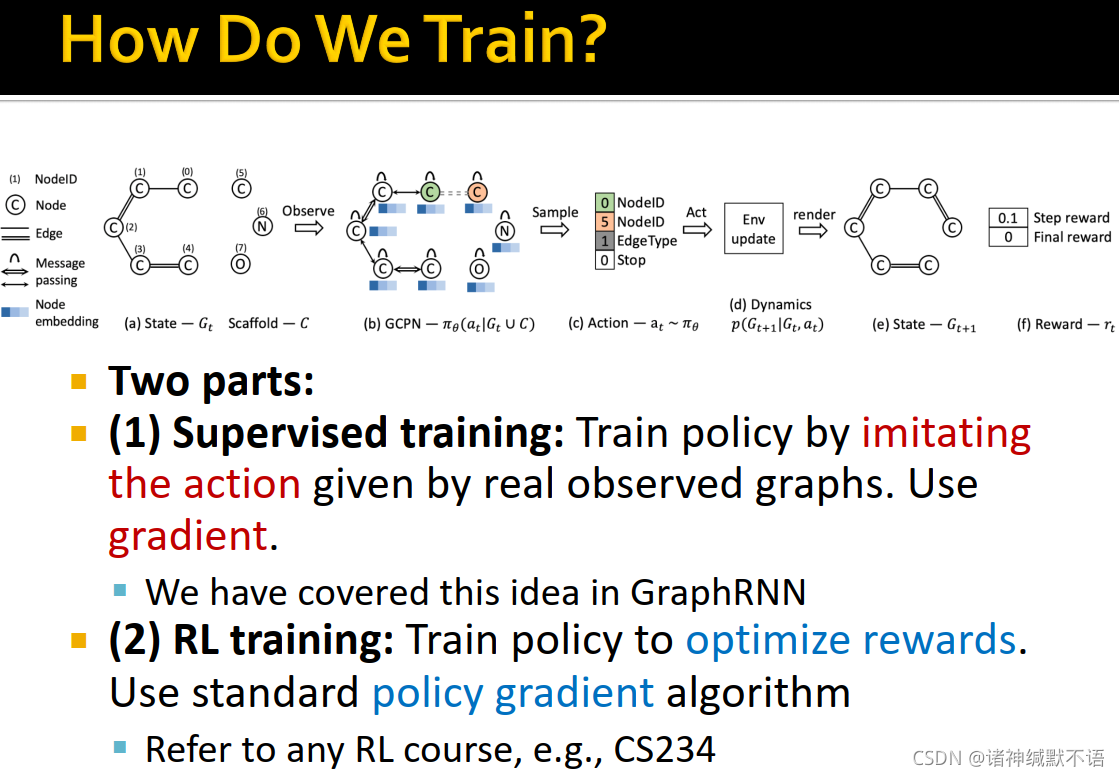
- 训练过程分两部分:
- 有监督训练:通过模仿给定被观测图的行为训练policy,用交叉熵梯度下降。(跟GraphRNN中的一样)
- 强化学习训练:训练policy以优化反馈,使用standard policy gradient algorithm。这一步我也不懂,它反正说可以参考CS234等强化学习课程来了解这部分。以后有缘再了解吧。
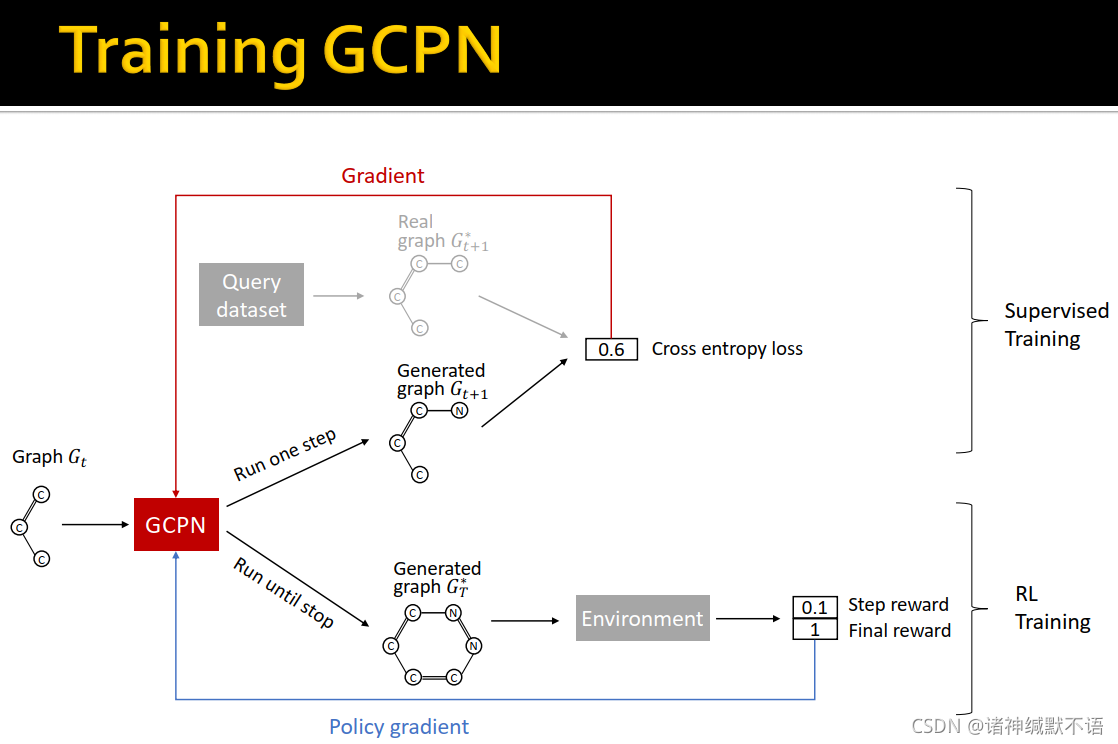
- GCPN实验结果
在logP和QED这些医药上要优化的指标上都表现很好:

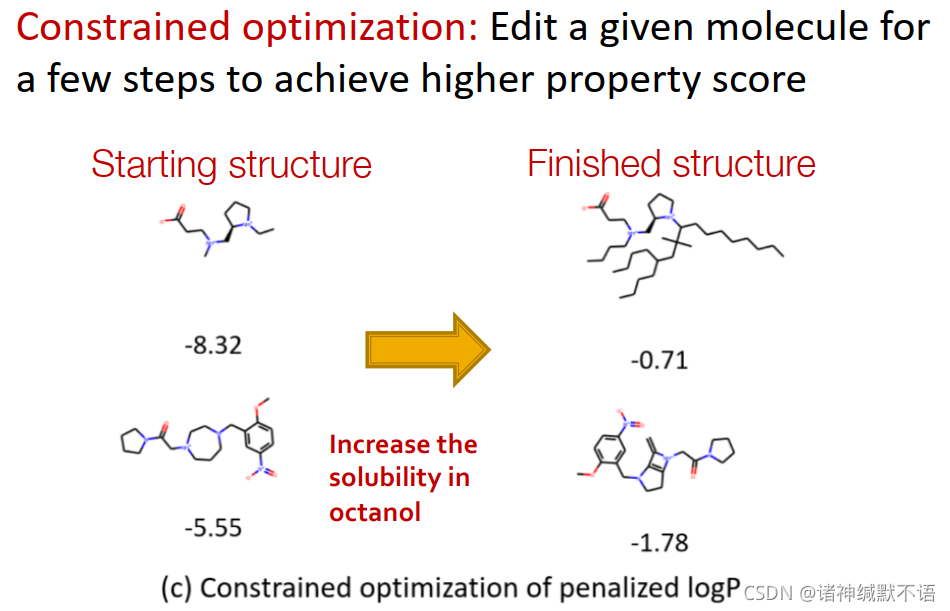
constrained optimization / complete任务:编辑给定分子,在几步之后就能达到高属性得分(如在以logP作为罚项的基础上,提升辛醇的可溶性):
5. 本章总结
- 复杂图可以用深度学习通过sequential generation成功生成。
- 图生成决策的每一步都基于hidden state。
hidden state可以是隐式的向量表示(因为RNN的中间过程都在hidden state里面,所以说是隐式的),由RNN解码;也可以是显式的中间生成图,由GCN解码。 - 可以实现的任务包括模仿给定的图数据集和往给定目标优化图。

GraphRNN: Generating Realistic Graphs with Deep Auto-regressive Models. J. You, R. Ying, X. Ren, W. L. Hamilton, J. Leskovec. International Conference on Machine Learning (ICML), 2018. ↩︎ ↩︎ ↩︎
Graph Convolutional Policy Network for Goal-Directed Molecular Graph Generation. J. You, B. Liu, R. Ying, V. Pande, J. Leskovec. Neural Information Processing Systems (NeurIPS), 2018 ↩︎ ↩︎
可参考我之前写过的笔记:cs224w(图机器学习)2021冬季课程学习笔记17 Traditional Generative Models for Graphs_诸神缄默不语的博客-优快云博客 ↩︎
我写过的cs224w笔记系列合集:cs224w(图机器学习)2021冬季课程学习笔记集合_诸神缄默不语的博客-优快云博客 ↩︎
可参考我之前写过的这篇笔记的第5个脚注:cs224w(图机器学习)2021冬季课程学习笔记3: Node Embeddings_诸神缄默不语的博客-优快云博客 ↩︎
noise distribution应该值得就是Gaussian noise(因为我谷歌搜索noise distribution出来的第一个链接就是Gaussian noise的英文维基百科页面) ↩︎
只简单看了一下:What is Teacher Forcing for Recurrent Neural Networks?
总之意思就是如课程中所说,用真实值而非上一cell的输出值作为下一cell的输入,效果会更好。至于具体为什么好的可以以后再研究吧。 ↩︎就这个我也查了一下……可以参考这篇文章:Understanding binary cross-entropy / log loss: a visual explanation | by Daniel Godoy | Towards Data Science
但是我写这玩意的时候有点困了,而且我懒得学这种基础知识了,所以我懒得看了,以后有缘再研究这些熵啊损失函数啊交叉熵啊二元交叉熵啊这种高级东西吧。 ↩︎其实我没看懂这个RNN中的time step是什么意思,总之把参考资料也列出来,以后有缘再研究:对循环神经网络(RNN)中time step的理解_Microstrong-优快云博客 ↩︎
但是我没搞懂这里为什么写是3个?我寻思这应该是它之前同层及前一层的节点数吧?为什么能是3?
至于图中提到的BFS frontier,我查看一下好像是个专有名词,是同一层已知但未访问节点集合的意思……然后我就:?
关于这个意思的参考资料(都没仔细看,以后有空可以研究研究):
① https://www.cs.dartmouth.edu/~scot/cs10/lectures/19/19.html
② Breadth First Search and Depth First Search | by Tyler Elliot Bettilyon | Teb’s Lab | Medium
③ 思考(9)BFS,DFS,A* and Dijkstra’s的区别与联系 - 知乎
④ Graph Search Algorithms
我看了原论文1 里的插图(没看内容),看说这个M确实可以是一个常数。就是我寻思啊,当然你可以手动限制M是一个常数,就卡死边RNN的cell数就可以了嘛。但是为什么会这样啊?它应该是这样吗?
我觉得对这一问题如果需要进行更深一步的了解,可能需要去深层阅读原论文及相关文献,所以我就……以后再说吧。 ↩︎这个orbit在原论文中是这样写的:

文中提及的参考文献就是这篇:Hocevar, T. and Demsar, J. A combinatorial approach to graphlet counting. Bioinformatics, 30(4):559–565, 2014.
一个orbit就是说在图上等价/自同构(graph automorphism)的所有节点所组成的一个集合这种东西。而这里的orbit count statistics应该就是同一节点数的orbit数的意思。当然我也不太确定,可以看看GraphRNN和上一段这个参考文献确认一下。 ↩︎其实我没搞懂这个问题的难点在哪,机器学习的所有有监督学习不都是默认目标的决定机制未知么,如果已知谁还用什么机器学习啊…… ↩︎
prediction head大概就是分类层前最后一层利用节点嵌入进行预测的这种感觉。
可参考我之前写的笔记:cs224w(图机器学习)2021冬季课程学习笔记10 Applications of Graph Neural Networks_诸神缄默不语的博客-优快云博客 ↩︎





 本文介绍了深度图生成模型的基础概念和关键技术,包括GraphRNN和GCPN两种模型。GraphRNN能够生成与给定图数据集相似的图,而GCPN则能够针对特定目标优化图结构。
本文介绍了深度图生成模型的基础概念和关键技术,包括GraphRNN和GCPN两种模型。GraphRNN能够生成与给定图数据集相似的图,而GCPN则能够针对特定目标优化图结构。

















 943
943

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










