硅基计划3.0 学习总结壹时间空间复杂度与泛型-优快云博客

1752388689448

文章目录

一、集合框架

它类似于C++中的STL容器，是对数据的组织形式，也是数据结构的一个重要思想
我们的学习路线是先理解底层原理，再去使用其工具去实现对应的算法

二、时间/空间复杂度

1. 时间复杂度

它是衡量算法运行速度的重要依据，对于时间复杂度我们不能说我们自己掐表计算，那样完全就是个人主观而忽视了客观
我们如何去计算呢？我们可以通过观察语句的执行次数去计算
这就要讲道我们的大O测算法了

2. 大O测算法

比如一个方法中有几很多种计算，就比如如下方法

public static int func(int n){
        int count = 0;
        for (int i = 0; i < n*n; i++) {
            count++;
        }

        for (int i = 0; i < n; i++) {
            count++;
        }

        for (int i = 0; i < 1000; i++) {
            count++;
        }

        return count;
    }

    public static void main(String[] args) {
        System.out.println(func(100));
    }

我们可以很清晰看到func()方法中有三种循环，一个是n*n，一个是n，另一个则是1000一个常数，而我定义count变量就是为了统计语句被执行了多少次vv
现在我们可以通过简单的加法得出，执行了 $n^{2} + n + 1000$ 次，难道这个就是时间复杂度了吗，并不是

关于大O测算法，我们有几个语法

如果变量式子中带有常数，我们要把常数项去掉

为什么？你想，随着变量N越来越大，它的增速是远大于常数项的，N趋于无穷的时候此时常数就没有意义了，它可以被忽视了

去除了常数项后，只保留高阶项

为什么？趋于无穷大的时候，高阶项增速远大于低阶项，当数字足够大的时候高阶项的数远大于低阶项，此时低阶项就没有意义了

去除低阶项之后，再去除高阶项的常数系数

这个就不用解释了，道理跟之前一样

提醒一点：如果式子中只有常数项，那就把常数项改成1，时间复杂度就是O(1)

因此我们之前得到的那个式子 $n^{2} + n + 1000$ 就可以简化成 $N^{2}$ ，即时间复杂度是O(N²)

还记得我们之前的冒泡排序吗，它的时间复杂度又是多少呢

public static void bubbleSortEnd (int [] array){
       for (int i = 0; i < array.length-1; i++) {
           boolean flag = false;
           for (int j = i+1; j <array.length-1-i ; j++) {
               if(array[i]>array[j]){
                   int temp = array[i];
                   array[i]= array[j];
                   array[j] = temp;
                   flag = true;
               }
           }
           if(!flag){
               return;
           }
       }
   }

我们知道冒泡排序本质上就是每排序一次，就少检查一个数字，外部循环循环了N次（对应内部循环的每一次）
内部循环第一次执行了N-1次，第二次执行了N-2次…最后到1次，排序完毕
因此总共执行了 $N - 1 + N - 2 + N - 3 + ...... + 2 + 1$ ，利用等差数列求和公式 $\frac{a_1+a_n}{2}$ 来求得最终结果 $\frac{n^2-n}{2}$ ，利用大O测算法规则化简成O(N²)

同样的思想我们用到二分查找上来看，本质上每检查一次，排查的范围就缩小了一半
也就是说第一次的范围是 $\frac{1}{2}^1$ ，第二次的范围是 $\frac{1}{2}^2$ …那第N次的范围就是 $\frac{1}{2}^N$ 了
因此我们的最终就是 $\frac{1}{2}^N$ 了，而我们要求的执行次数N可知为 $log_2N$ ，简写成 $\log N$ ，以后我们不写下标默认就是 $log_2$ 为底的对数

同样地，我们去讨论斐波那契数，对于递归算法计算起来比较麻烦，不过大致就是 $递归次数\times每一次递归后内部语句的执行次数$

public static int feb(int num){
        if(num<=2){
            return 1;
        }else{
            return feb(num-1)+feb(num-2);
        }
    }

好，那我们分析，比如求斐波那契数的第四个数，我们来画图

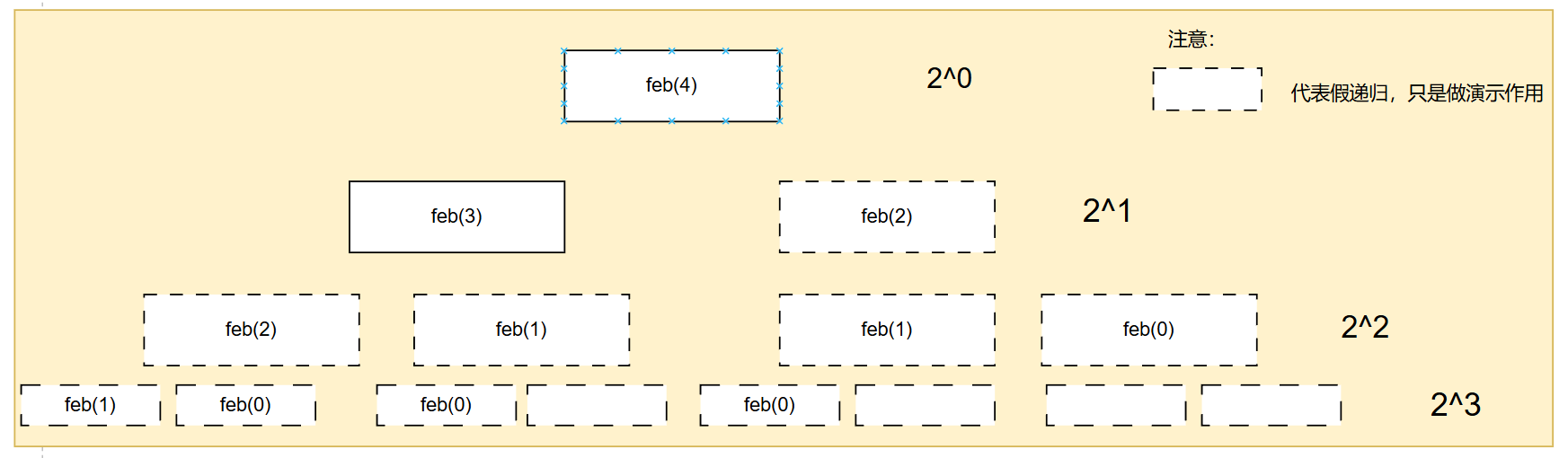
从图片中我们可以看到，递归一次就是 $2^0$ ，递归两次就是 $2^1$ …递归N次就是 $2^N$ ，因此我们使用等差数列求和公式最后求得 $2^N-1$ ，根据大O算法规则简化成O(2^N) `

看到这里，你可能会抬杠，说哎呀如果我数组一开始有序，那我是不是只要遍历数组就好了，那我执行次数就很少啊
你说得对，但是我们的时间复杂度都是以最复杂的情况去衡量的，它都是最坏的情况了，那如果现在时间复杂度比它小那就再好不过了

3. 空间复杂度

跟时间复杂度类似，算的就是变量的个数，遵循大O测算法
即临时占用的存储空间，就比如刚刚的递归算法，每一次递归都要临时开辟一块新空间，那递归N次，空间就开辟了N次
因此斐波那契数递归的空间复杂度就是O(N)

4. 常见的复杂度

$O(1)，O(\log N)，O(N)，O(N\log N)，O(N^2)$ ，它们本质上都是函数

三、包装类型

就是把每个基本的数据类型整理成包装类，比如char–>Character，int–>Integer，long–>Long等等

1. 装箱（包）

就是把基本数据类型包装转换成包装类型

int a = 10;
Integer i = a;

这个就是自动装箱，表面没有调用任何方法（但是底层调用了）
我们可以来看看反汇编码

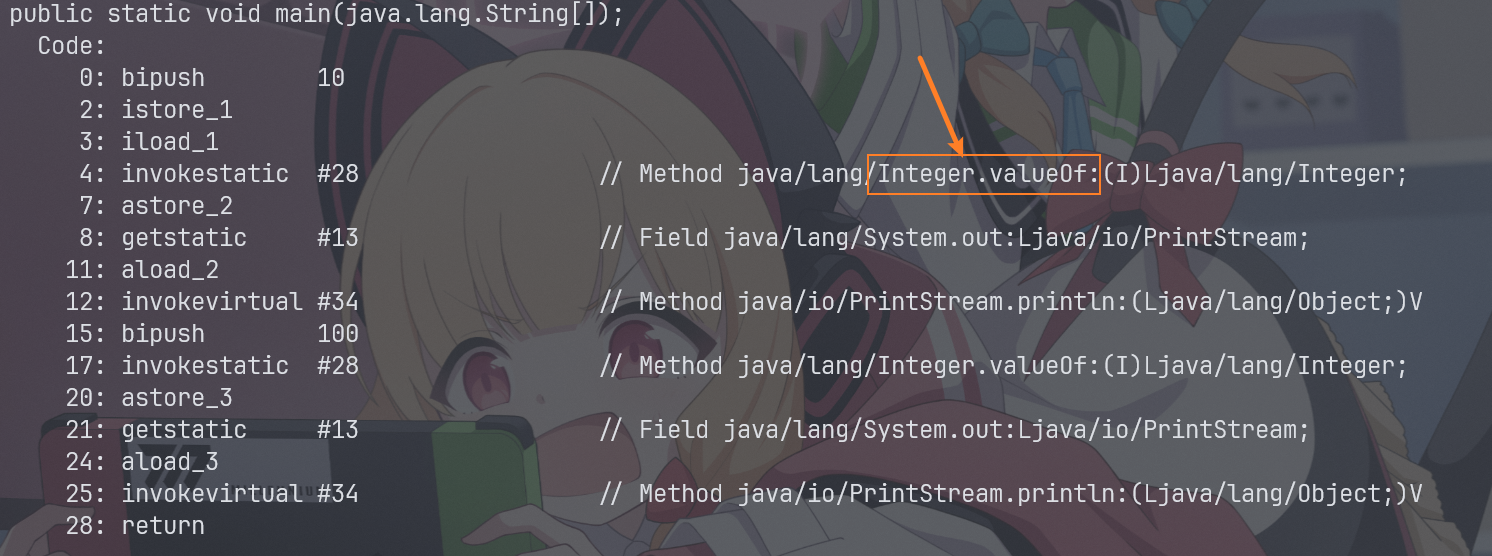
Integer j = Integer.valueOf(100);

这个就是手动装箱，调用了Integer类中的valueOf()方法

2. 拆箱（包）

既然能装上，那就能拆下来

//自动拆箱
Integer i = 100;
int a = i;
//手动拆箱
int b = i.intValue();
//甚至还可以指定其他类型拆箱
double b = i.doubleValue();//结果是100.0

3. 拆箱装箱经典问题

Integer a = 120;
Integer b = 120;
System.out.println(a == b);//true
Integer i = 130;
Integer j = 130;
System.out.println(i == j);//false

为什么打印的结果一个是True一个是False呢，我们可以点开valueOf方法的原码看看

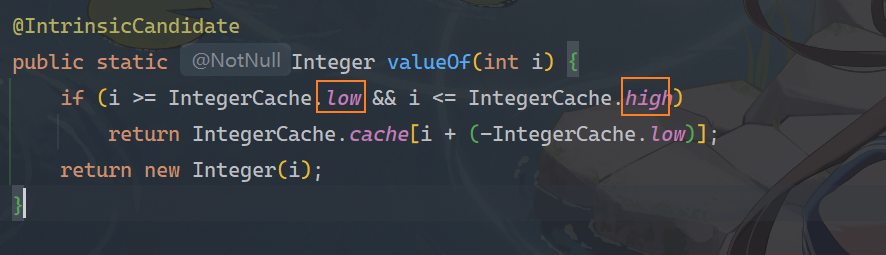
我们看到它是有一个范围的，如果超过了这个范围就new对象，当然新旧对象之间就不相等了
我们查看low和high值，其分别为-128和127，也就是说我们130超过了这个范围，自然就new对象了，自然判定就是false
但是120并没有超，我们看到它是把120存入了一个缓存数组中，这个数组的大小就是256即对应下标0~255
如果我们传入120，那对应的就是数组 $120 + (- - 128)$ ，下标就是228，因此当变量值b传入120时，缓存数组找到了相同的值，地址都一样，那在比较的时候自然就是true了

四、泛型

说白了就是一个类可以适应很多类型，类似于C++的模板类

1. 非泛型

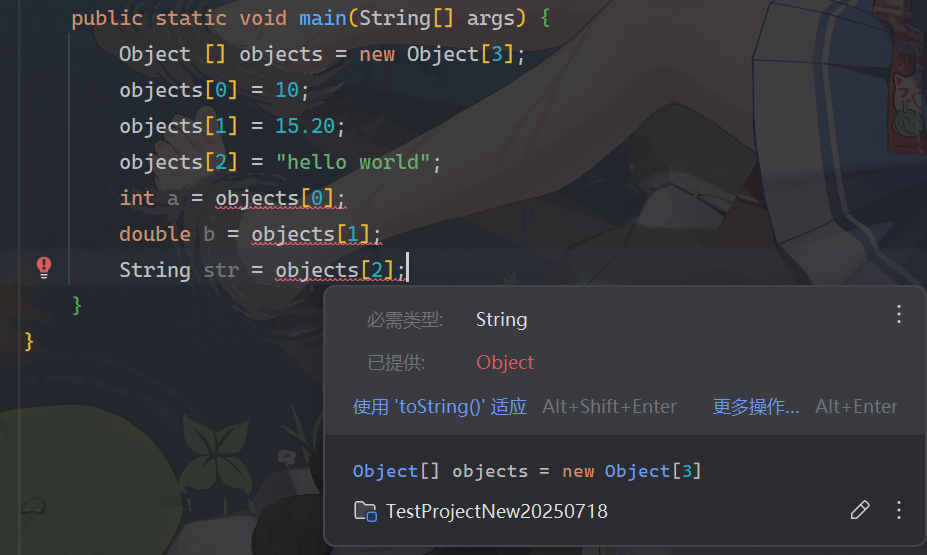
虽然Object类数组什么都能存，但是读取的时候还是要强转成对应类型，麻烦

2. 泛型类

public class Try <T>{
    public Object [] objects = new Object[4];

    public void funcB(int pos,int num){
        this.objects[pos] = num;
    }

    public T funcA(int num){
        return (T)this.objects[num];
    }

    public static void main(String[] args) {
        Try<Integer> a = new Try<>();
        a.funcB(1,14);
        System.out.println(a.funcA(1));
    }
}

可以看到我们给类名后面加上了<T>占位符，表示后续的数据类型，然后在类中定义了Object数组，给了对应的funcA和funcBt方法
可以看到在return的时候还是需要强转成指定的占位符<T>的类型，但是此时在main方法中并不会报错了，在new的时候<>中的包装类可以不写
但是这里要说明一点，泛型参数需要的是包装类，基本数据类型是不行的
泛型之间还可以有多个占位符，还可以继承，感兴趣的可以去试试
当你明确了数据类型后，也就明确了这个容器可以存什么数据类型，而因此其他数据类型就存储不了

3. 泛型运行编译

1. 擦除机制——泛型的意义

指的就是在运行的时候把泛型去掉，因为泛型指的是在编译的时候才存在的概念
此时泛型就会填换成边界类比如Object类
我们刚刚的代码在编译的时候就被替换成Object类
但是此时是运行的时候的Object类而并非编译的时候，因此类型就已经检查过了，就比较安全，这就是泛型的意义

2. 桥接方法

//一串代码类型擦除后的代码如下
public class Node {
  Object data;
  public void setData(Object data) {
    this.data = data;
    }
  } 
public class StringNode extends Node {
  public void setData(String data) {
    super.setData(data);
  }
}

你会发现子类和父类的同名方法不一样，不能构成重写呀
但是此时在子类StringNode中编译器会默认生成一个我们看不到的方法，以此来构建子父类的同名方法之间的关系
说白了就是这个代码重写了父类Node的同名方法，然后又去调用了子类StringNode的同名方法

public void setData(Object data) {
  setData((String) data);
}

3. 泛型边界

我们在使用泛型的时候可以明确其传入类型的边界

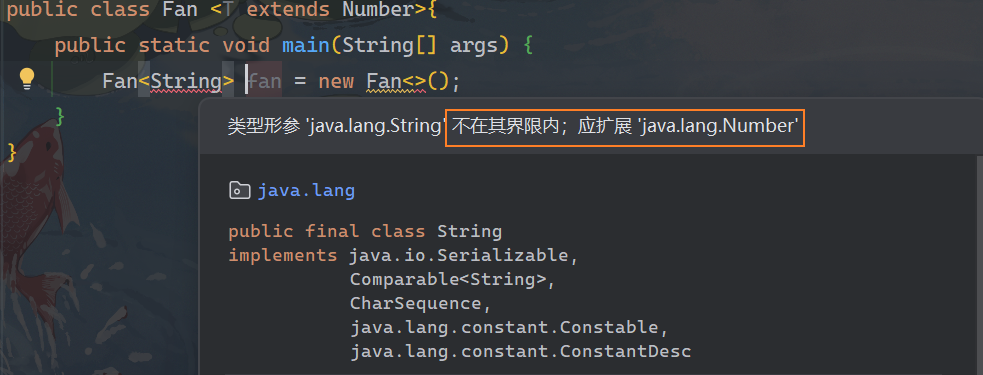
我们可以看到String类不可指定，因为我们指定了Number类及其子类作为指定类型
而在Number类及其子类中并无String类

当然我们没有写边界的时候默认就是Object类，之前的代码也有提现（边界擦出后是Objet类）
或者是你传入的类型要实现什么类型的接口，比如public class Fan <T extends Comparable<T>>
当然还可以有多个边界<T extends 类1,E extends 类2......>以及多重边界<T extends A类&B类>

4. 泛型方法

可以通过对象去访问，调用的时候直接通过对象去调用

public class Fan <T extends Number> {
    public <T> T find(T [] array){
        return array[1];
    }

    public static void main(String[] args) {
        Fan<Integer> fan = new Fan<>();
        Integer [] array = {1,4,8,9};
        System.out.println(fan.find(array));
    }
}