硅基计划 练习 汉诺塔和斐波那契数中青蛙跳台问题

 

---

汉诺塔问题

一、问题定义

经典的递归问题，问题描述为：有三根柱子，A、B、C，A柱子上有n个盘子，盘子从上到下按大小顺序排列，目标是将所有盘子从A柱子移动到C柱子，移动时遵循以下规则：

1. 每次只能移动一个盘子
2. 任何时刻大盘子不能再小盘子

二、问题思考

1.我们先假设有三个塔，分别交A,B,C，我们目标是把全部盘子移动到C塔上

我们在A塔上有几个盘子，假设只有一个，那我们是不是可以直接移动到C塔

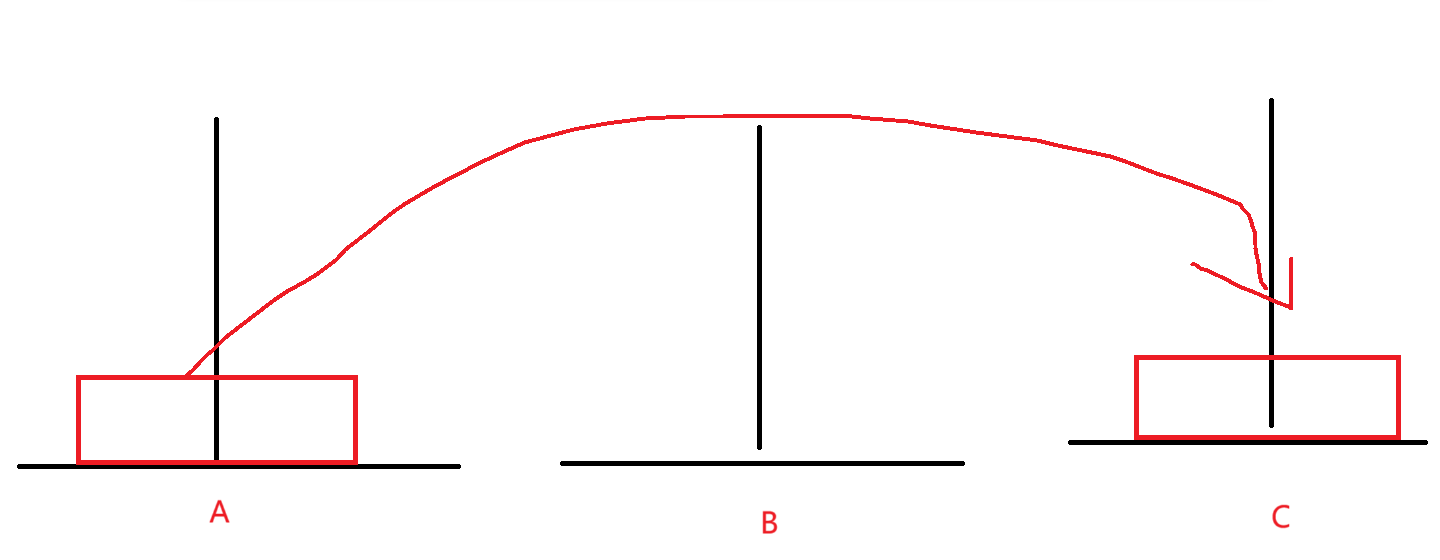
假设有两个，那我们先把小的盘子移到B上，再把大的移到C上，再把B上小的移到C上

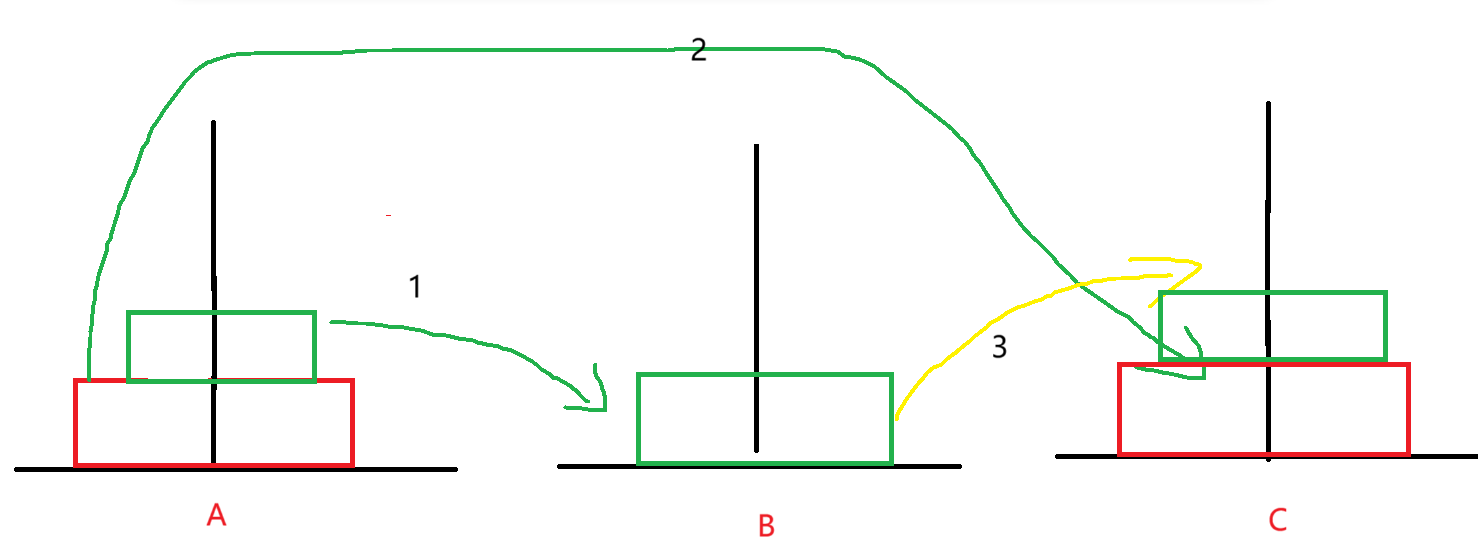
假设有三个，那我们同理把最小的移到C上（不能移到B，因为后续的话无法继续移到更小的盘子） ，再把第二小的移到B上，再把C上的移到B上，以此类推......

##但是你有没有想过，这样是不是太复杂了，假设我们有三个盘子，我们是不是可以把最后一个盘子和其他盘子的盘子各看成一个整体，那我们是不是相当于只有两个盘子了，那我们移动以后，我们再移动剩下两个盘子，以此类推，直到一个盘子，最后完成

诶，这就是我们今天讲的终点，这就符合了我们递归的思想，我们来实现代码，我给予完整代码展示，上面都有对应注释，应该基本上都能看懂

三、问题实现&代码展示

void move(char pos1, char pos2)//这个是用来展示移动盘子的函数
{
	printf("%c→%c ", pos1, pos2);
}

void game(int n,char pos1,char pos2,char pos3)//三个塔我们对应三个数组来接收
{
	if (n == 1)
	{
		move(pos1, pos3);//倘若只有一个盘我们直接移动就好
	}
	else
	{
		game(n - 1, pos1, pos3, pos2);//三个数组对应起点，中转站，目的地终点
		move(pos1, pos3);//此时我们再把最后一个盘子移动到C塔
		game(n - 1, pos2, pos1, pos3);//三个数组对应起点，中转站，目的地终点，此时再递归剩下的n-1的盘子
	}
}
int main()
{
	int input = 0;
	scanf("%d", &input);
	game(input, 'A', 'B', 'C');//传参，并且命名三个塔
}

##有一点我要强调，如果你太细究递归细节，反而你会一团乱麻，所以我们理解基本原理就好，至于太细节的东西，就让电脑去明白吧，我们负责写就好了。

---

斐波那契数中青蛙跳台问题 

一、问题定义

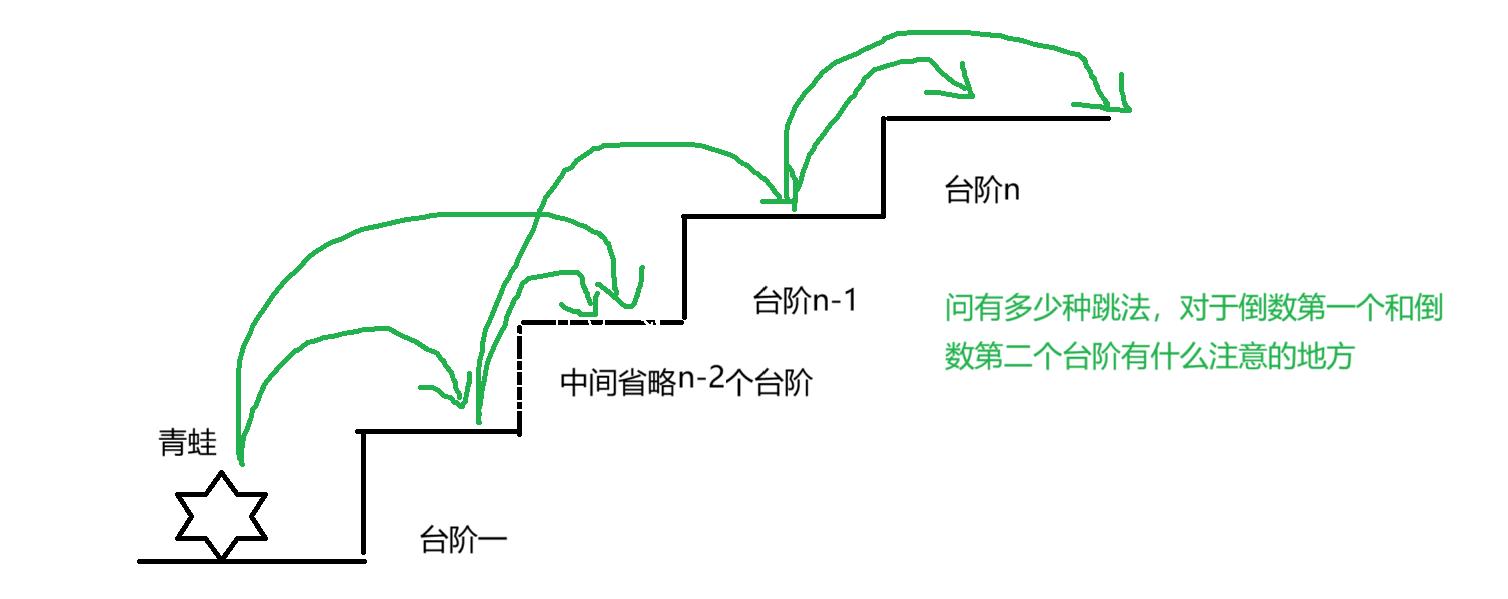
描述的是一只青蛙一次性可以跳一个或者两个台阶，问调到第n个台阶有多少种跳法

二、问题思考

1.我们首先来思考问题

假设青蛙从第一个台阶起跳调到第二个台阶，那么就有一种跳法

从第二个台阶起跳调到第三个台阶，有一种跳法

从第一个台阶跳上第三个台阶，就有两种跳法了，第一种是从第一个跳到第三个，第二种是从第一个跳到第二个再跳到第三个

我们以此类推.............

我们很容易发现

那这样我们是不是可以转化成斐波那契数，因为第n个台阶跳法等于前两个台阶跳法之和

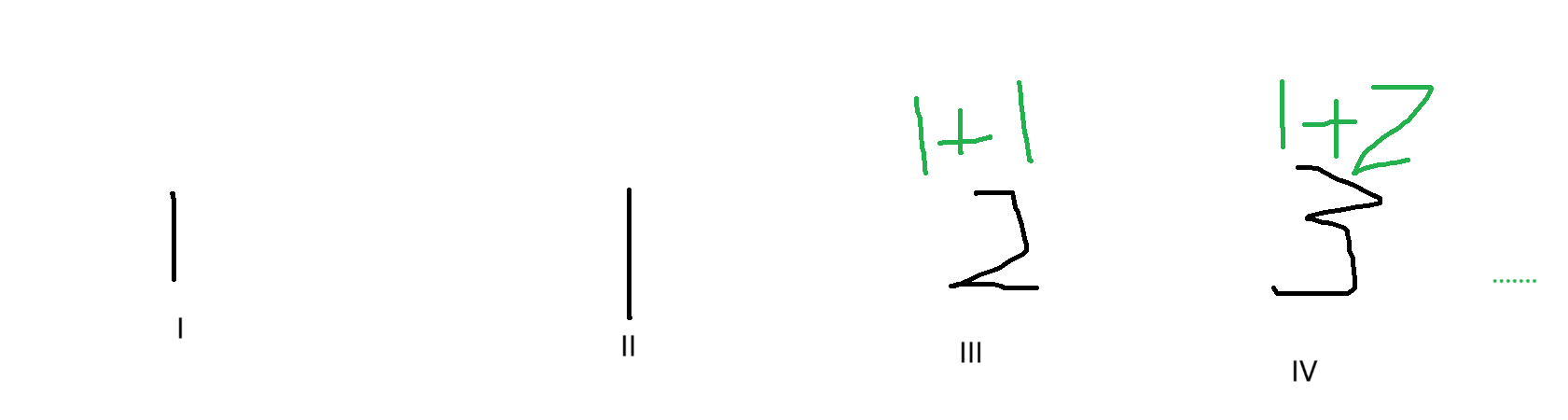
 三、问题实现&代码展示

int get_true(int x)
{
	if (x == 0)
		return 0;
	if (x == 1)
		return 1;
	if (x == 2)
		return 2;
	int a = 1;//前第二次跳法数
	int b = 2;//前第一次跳法数
	int c = 0;//当前跳法数
	for (int i = 3; i <= x; i++)//为什么循环终止条件式等于x呢？因为你输入第三个台阶，需要计算第三个台阶跳法数，
	{
		c = a + b;//前两次次数之和
		a = b;//更新值
		b = c;//同理更新值
	}
	return b;
}

int main()
{
	int input = 0;
	printf("请输入跳入的台阶数:>");
	scanf("%d", &input);
	int ret = get_true(input);//不需要偏移，不用像数组一样下标从0开始
	printf("%d", ret);
	return 0;
}

---

如果你还有其他更好的点子，欢迎和我交流

如果我有错误，欢迎指正

我们一起进步 

---

END