【机器学习笔记】无监督学习 聚类 K-means

1. 简介

前面讲到的回归就是一种典型的监督学习算法，需要我们标注数据集和期望结果集。但是日常生活中往往没有准确的期望值给我们，比如说我如何在上万文章中分类？同一文章所属的类别可否不同？这些问题使用回归就无法很好的给出解释并预测新结果，这时候就需引入无监督学习，即是没有明确的目标，通过给出的数据集发现其中潜在的规律🧐

---

而聚类就是典型的一个无监督学习算法，通俗点来讲就是将数据集分成一类一类，怎么分？分成几类就是我们下面要讨论的问题
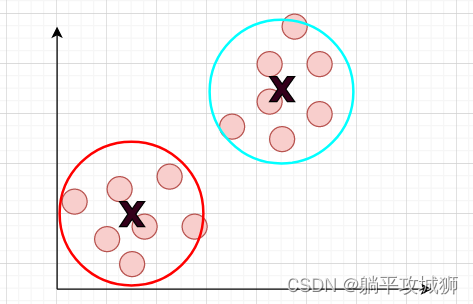
如下图例子，初始都是没有标签的数据，我们需要根据K-means算法（假设K=2）聚合成如下两类，当然不一定准确，毕竟没有标准的答案检测

2. K-means

说到聚类，那肯定逃不了K均值算法。该算法可以自动的将相似数据集分成一类，下面我们就来学习一下算法的思想

• 确定初质心 $K_1{K}_2{K}_3...$（比如说我分成2类，然后每一类的中心点就是质心）
• 不断重复，直到拟合
  – 遍历数据集，设置每一个数据到离其最近的质心下
  – 重新定位质心，即是用质心所包含的数据点求均值 $(x_j^{(1)}\_mean,x_j^{(2)}\_mean)$ 然后重新赋值

由于无监督的，所以结果有时候可能不会达到理想期望，所以实际应用中会多随机几个初始质心并，通过找到所有情况里最小的代价函数来确定用哪一个（一般50~1000次找一个最优解）

下面就来细讲一下上面两步是怎么实现的

2.1 寻找最近的质心

给定了一个初始的质心集合K（注意质心的个数不能多于样本点），其于任意一个样本点的距离一般用两点间距离公式计算，比如第 $i$ 个样本点与第 $j$ 个质心点的距离如下表示（假设二维）$$distanc{e}_{(X^{(i)}->K^{(j)})}=\sqrt[]{(X_0^{(i)}-K_0^{(j)}{)}^2+(X_1^{(i)}-K_1^{(j)}{)}^2}$$通过计算离每个样本点最近的质心并记录下来，为下一步分类做准备（当然该公式也可以作为一个代价函数，在上面提到的随机不同初始质心的情况下用于寻找最优解）

上述计算代码如下

def find_closest_centroids(X, centroids):
    """
    Computes the centroid memberships for every example
    
    Args:
        X (ndarray): (m, n) Input values      
        centroids (ndarray): k centroids
    
    Returns:
        idx (array_like): (m,) closest centroids
    
    """

    # Set K
    K = centroids.shape[0]

    # You need to return the following variables correctly
    idx = np.zeros(X.shape[0], dtype=int)

    for i in range(X.shape[0]):
        index = -1
        min_distance = float("inf") #初始化无穷大距离
        
        for j in range(K):
        	#向量相减 norm函数默认求各个位置的平方和再相加，即两点间距离公式
            cur_distance = np.linalg.norm(X[i] - centroids[j])  
            
            if(cur_distance < min_distance):
                min_distance = cur_distance
                index = j
                
        idx[i] = index  #np.argmin(distance)
    
    return idx

值得注意的是我们在计算的时候引入了numpy自带的函数norm，从而简化计算

norm函数讲解

基本语法

norm(x, ord=None, axis=None, keepdims=False)

各个参数的意思

x：输入值（可以是向量或矩阵）。
ord：范数类型，默认为None。常见的范数类型包括：
    None：默认为2范数。 
    0：零范数（非零元素的个数）。
    1：一范数（绝对值之和）。
    2：二范数（平方和开平方）。
    np.inf：无穷范数（最大绝对值）。
    -np.inf：负无穷范数（最小绝对值）。
    其他数值：对应的范数（绝对值的p次幂求和后开p次方）。
axis：指定沿哪个轴计算范数，默认为None（整个数组的范数）。可以指定一个轴或一对轴，例如axis=0或axis=(0, 1)。
keepdims：布尔值，是否保持结果的维度。默认为False。

2.2 计算质心平均值

上面分好每个质心对应的样本点后，下面就要重新计算质心位置来贴近这些样本点，而计算方法也很简单，就是将属于一个质心的所有样本点做均值，得到的结果即使该质心的新坐标。计算公式可以写成$$K^{(i)}=\frac{1}{n}\sum _{i\in c_k}{X}^{(i)}\text{其中ck是第i个质心下的所有样本点}$$将该步骤抽象为方法对应的代码如下所示

def compute_centroids(X, idx, K):
    """
    Returns the new centroids by computing the means of the 
    data points assigned to each centroid.
    
    Args:
        X (ndarray):   (m, n) Data points
        idx (ndarray): (m,) Array containing index of closest centroid for each 
                       example in X. Concretely, idx[i] contains the index of 
                       the centroid closest to example i
        K (int):       number of centroids
    
    Returns:
        centroids (ndarray): (K, n) New centroids computed
    """
    
    # Useful variables
    m, n = X.shape
    
    # You need to return the following variables correctly
    centroids = np.zeros((K, n))
    
    for i in range(K):
        mean_value = np.zeros(n)
        mean_count = 0
        
        for j in range(m):
        	#判断是否属于该质心	
            if(idx[j] == i):
                mean_value += X[j]
                mean_count += 1
        
        centroids[i] = mean_value/mean_count #计算均值
    
    return centroids

完成了这两部，对K_means的实现基本上就讲完了，最后再来讲一个问题初始点怎么选择？

3. 初始点选择

• 法一： 纯随机
• 法二：以随机的K个样本点作为K个质点的坐标

这两种方法其实都会导致局部收缩的现象，可能结果不是那么的贴合我们所想的，这时候就需要通过增加重随的次数来取他们之间的一个最优解。这里我们就以法二作为选取初始点的方法，

def kMeans_init_centroids(X, K):
    """
    This function initializes K centroids that are to be 
    used in K-Means on the dataset X
    
    Args:
        X (ndarray): Data points 
        K (int):     number of centroids/clusters
    
    Returns:
        centroids (ndarray): Initialized centroids
    """
    
    # Randomly reorder the indices of examples
    randidx = np.random.permutation(X.shape[0])
    
    # Take the first K examples as centroids
    centroids = X[randidx[:K]]
    
    return centroids

4.最终调用

调用我们的K-means输入相关参数得到分类拟合后的质心 老师的参考代码如下，也就是我们前面分析的步骤

def run_kMeans(X, initial_centroids, max_iters=10, plot_progress=False):
    """
    Runs the K-Means algorithm on data matrix X, where each row of X
    is a single example
    """
    
    # Initialize values
    m, n = X.shape
    K = initial_centroids.shape[0]
    centroids = initial_centroids
    previous_centroids = centroids    
    idx = np.zeros(m)
    
    # Run K-Means
    for i in range(max_iters):
        
        #Output progress
        print("K-Means iteration %d/%d" % (i, max_iters-1))
        
        # For each example in X, assign it to the closest centroid
        idx = find_closest_centroids(X, centroids)
        
        # Optionally plot progress
        if plot_progress:
            plot_progress_kMeans(X, centroids, previous_centroids, idx, K, i)
            previous_centroids = centroids
            
        # Given the memberships, compute new centroids
        centroids = compute_centroids(X, idx, K)
    plt.show() 
    return centroids, idx