
信噪比定义
信噪比SNR是衡量信号质量的一个重要指标,是指有用信号功率与噪声功率的比值。信噪比越高,说明信号质量越好,波形在示波器上显示的效果会更加清晰,测量结果更能真实反映被测信号的特性;信噪比越低,说明信号质量越差,信号细节会被掩盖,波形显示会有抖动或线条粗大等问题,造成的测量误差可能会导致误判。
提高信噪比
使用示波器进行电子测量测试时,可以采用以下方法使波形更加清晰、稳定,以此提高信噪比,以下以品致MDO7500A为例介绍操作:
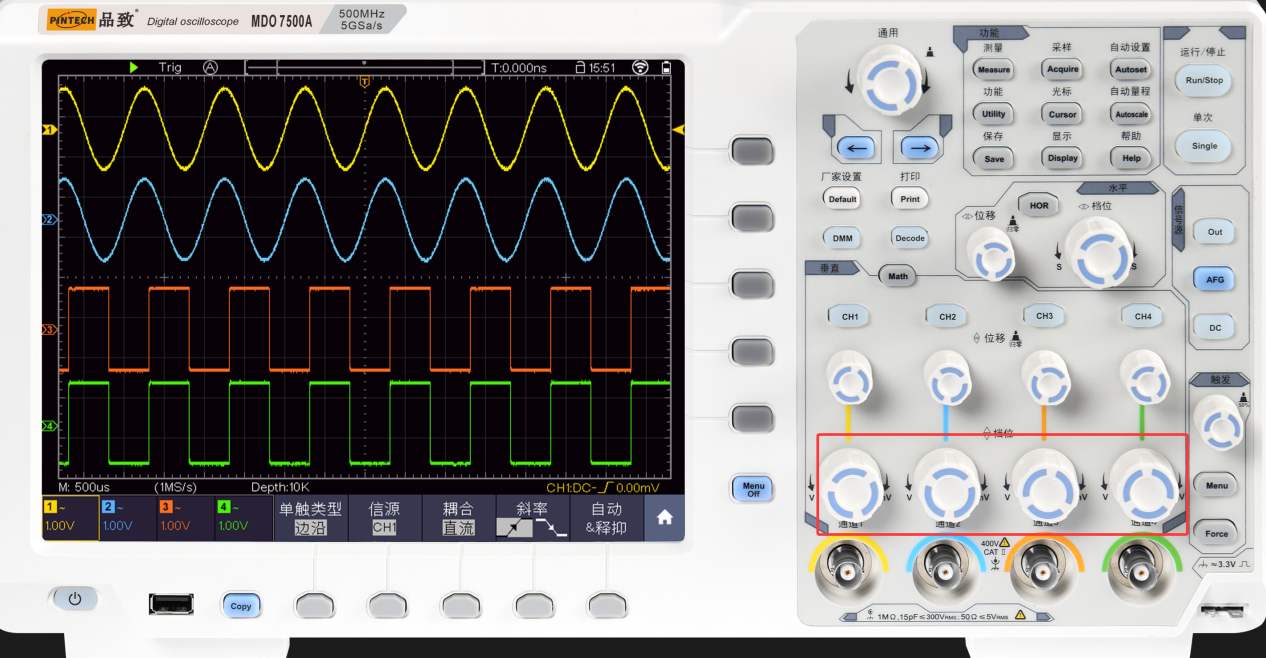
1、选择合适的垂直量程
选择合适的量程范围可以避免信号失真和降低误差。量程选择过大,波形过小,示波器的ADC精度未完全利用,误差将变大;量程选择过小,波形容易超出屏幕,导致无法获取幅值等信息。选择调整垂直量程让波形占据示波器整个屏幕的60%~80%垂直空间,使信号细节更加清晰,从而降低误差,提高测量准确性。具体操作是:转动垂直量程旋钮初步调整量程,若波形未居中显示,再通过垂直位移旋钮将波形移至屏幕中间区域,随后再次微调量程,直至波形相对居中且占据 60% 以上垂直空间,确保信号观测与测量的有效性。
2、带宽限制
示波器前端放大器与 ADC 的宽带特性极易引入高频噪声,而被测信号通常有明确的频率上限,此时可以选择使用示波器的带宽限制功能,通过一个低通滤波器衰减高频分量,保留低于截止频率的有用信号。该型号带宽限制(BW Limit)功能是单选20MHz,在输入通道的对应功能区,按下通道对应按钮即可找到。
3、使用平均采样模式
噪声往往是无规律的随机信号,假如被测信号是周期信号,可以选择使用示波器的平均采样功能,让信号波形更加稳定和清晰,从而提高信噪比。示波器通过对多次捕获的波形进行点对点平均,周期信号因为其相关性将被增强,噪声会因为其随机性被抵消而衰减。选择采样(Acquire)按钮--平均采样(Average)功能,从小到大选择合适的平均计算次数,直至波形变得清晰。
上述方法围绕 “突出有用信号、抑制噪声干扰” 的逻辑展开,实际操作中可依据被测信号的频率特性、周期性等具体情况组合使用,从而有效提升信噪比。




















 4793
4793

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








