二进制-我的理解_685转换成二进制-优快云博客

本文介绍了数字进制的概念，特别是二进制系统。二进制作为一种满2进位的计数方式，由1和0两个数字构成，广泛应用于计算机领域。其简单运算规则、与电路状态的对应关系以及在数据表示和存储中的优势使得二进制成为现代计算机的基础。此外，还阐述了二进制与十进制间的转换方法。

二进制，单看名字，就可以联想到我们从小就学习的十进制，十进制是满10进位，用数字0-9记数的计数方式，那么二进制就是满2进位的计数方式了，满2进位，只有1和0两个数字进行记数。总的来说，二进制和十进制都属于数字进制的一部分。

数字进制

数字进制是一种记数方式，利用这种记数的方法，我们可以使用有限的数字符号来表示所有的数值。

面对不同的使用场景，我们会根据便利性来使用不同的进制。比如我们常用的10进制、计算机领域使用的2进制。而2进制和10进制中的2和10都是称为对应进制里面的基数。

基数，顾名思义有一种基础、基石的意思。若一个进制的基数是2，就是2进制；若一个进制的基数是10，就是10进制；若一个进制的基数是N，那么就是N进制。

再来看看进位计数方式：

（1）10进制：满10进1位，如有一个数685，

写成算式就是：6x100+8x10+5x1=685。

其中，我们从0位开始，10的0位就是10的0次方，为1，使用0-9的数字，我们可以乘出5，但是无法计算出剩余的680，这时需要我们进一位到10的1次方，为10，我们可以得出80，以此类推，我们使用了10的2次方，100，得出了600。我们把所得都加起来，5+80+600，就可以得出我们设定的数字685了，写成算术式：

685 = 6x $10^{2}$ + 8x $10^1^{^{^{^{}}}}$ + 5x $10^{0}$

（2）2进制：满2进1位，就像上面的数字685，

写成算式就是：1x512+0x256+1x128+0x64+1x32+0x16+1x8+1x4+0x2+1x1=685

遇上同理，从0位开始，2的0次方为1，使用1和0，只能得出1，剩余的684得继续通过进位来获得满足的数字【这种方法后面会说到】，写成算数式：

685 = 1x $2^{9}$ + 0x $2^{8}$ + 1x $2^{7}$ + 0x $2^{6}$ + 1x $2^{5}$ + 0x $2^{4}$ + 1x $2^{3}$ + 1x $2^{2}$ + 0x $2^{1}$ +1x $2^{0}$

由上结果，我们可以知道n进制的进位计数方式，比如有b个数字，如果a3、a2、a1、a0是其中四个数字，我们可以写成这种形式：

a3a2a1a0 = a3x $b^{3}$ + a2x $b^{2}$ + a1x $b^{1}$ + a0x $b^{0}$ (a3a2a1a0不是相乘，只是一个序列)

目前我们常见以及常用的进制有：10进制、2进制（计算机领域）、8进制（计算机领域）、16进制（计算机领域）、6进制（骰子）、12进制（一打12个）

二进制

如前面所说，2进制只用1和0两个数字进行记数，在计算机领域，由于计算机大部分是由集成电路组成，而电路的状态总的来说只有两种状态：开和关，正好可以对应1和0，所以我们可以根据这种特性来对电路进行有目的性的驱动，从而实现某个功能，这也是现代的计算机和依赖计算机的设备都使用二进制的原因。

使用二进制还有其他的优点：

1、二进制的四则运算规则十分简单，满1进位，有利于简化计算机内部结构，提高运算速度。

（1）加： 0 + 0 = 0 ，1 + 0 = 1 ，0 + 1 = 1 ，1 + 1 = 10

（2）减： 0 - 0 = 0 ，1 - 0 = 1 ，1 - 1 = 0 ，10 - 1 = 1

（3）乘： 0 x 0 = 0 ，0 x 1 = 0 ，1 x 0 = 0 ，1 x 1 = 1

（4）除： 0 / 1 = 0 ，1 / 1 = 1

2、使用二进制表示数据，抗干扰能力强，可靠性高，因为每位数据只有高和低两个状态，当数据受到一定程度的干扰，我们仍能可靠地分辨出数位是高还是低；

3、逻辑代数是逻辑运算的理论依据，二进制只有0和1两个数码，正好与逻辑代数中的和“false”和“true”相吻合。

4、二进制与十进制之间的转换简单，下面讲下10十进制的数是如何转换为二进制的，如上面的685：

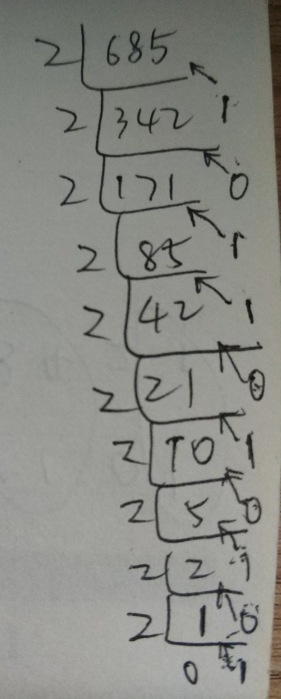
如上图所示，我们对685进行不断的对2取余，我的箭头所指表示前一个被除数的余数，所以最后的1也要对2取余，直到为0，然后从最下面开始按顺序往上排列，得出来的就是685转换为2进制后对应的值：

685(10) = 1010101101(2) 【括号内表示的为进制】

那么2进制的数又是如何转换为10进制呢？咱们来看2进制的位数，如上 1010101101 ，总共有10位，我们从右往左，以0位开始，对应2进制的每一个位数（刚才所得的各个余数）进行乘积，再相加，写出来就是：

1010101101(2) = 1x $2^{9}$ + 0x $2^{8}$ + 1x $2^{7}$ + 0x $2^{6}$ + 1x $2^{5}$ + 0x $2^{4}$ + 1x $2^{3}$ + 1x $2^{2}$ + 0x $2^{1}$ +1x $2^{0}$ = 685(10)

也就是前面那个公式啦~

在计算机领域，结合2进制和电路的逻辑，2进制的0或者1，就对应一个位，位（bit）是数据存储的最小单位。8bit就代表一个字节（Byte），比如10101010，这里就是代表一个字节的数据。咱们平常所说的计算机CPU位数，就是指CPU一次能处理的最大位数。例如64位计算机的CPU一次最多能处理64位数据。这个位就是相对于2进制的0和1而言。