线性神经网络
介绍
线性神经网络和感知机的区别不大,只是把激活函数由y=sign(x)变成了purelin函数y=x。
为什么要改激活函数呢?
感知机是通过误分类点来不断修改权值,这样会导致最终的超平面虽然的确完成了分类的任务,但是它未必分的那么‘平均’。
我们希望那些已经正确分类的点也会对权值产生影响。
感知机那块我们的目的是找出合适的权值w,使得最终sign(wx)的值与实现给定的y值一样,就算训练完了。
但是现在不是y=sign(x)了,而是y=x,那怎么办呢?
δ\deltaδ学习规则
wx的值虽然可能无法和y一模一样,但是我们可以让它最小。
E=12(y预−y真)2=12(f(wX)−y)2
E=\frac12(y_预-y_真)^2=\frac12(f(wX)-y)^2
E=21(y预−y真)2=21(f(wX)−y)2
就是让代价函数E最小。
w的迭代函数就是
w:=w−η∂E∂w
w:=w-\eta \frac{\partial E}{\partial w}
w:=w−η∂w∂E
我们来求下导可以得到
E′=XT(f(wX)−y)f′(wX)
E'=X^T(f(wX)-y)f'(wX)
E′=XT(f(wX)−y)f′(wX)
将(f(wX)−y)f′(wX)(f(wX)-y)f'(wX)(f(wX)−y)f′(wX)就成为δ\deltaδ(delta)。
对于y=x而言,显然δ\deltaδ为f(wX)-y。
w:=w−ηXT(f(wX)−y)
w:=w-\eta X^T(f(wX)-y)
w:=w−ηXT(f(wX)−y)
没错和感知机那块是一样的,但 f(wX)-y 可不是只有2或-2两种结果了。
线性神经网络解决异或问题
直线肯定是分不开的,我们用曲线,策略和多项式回归一样,多加几个非线性项。
异或有两个特征a和b,我们就把a2a^2a2,b2b^2b2,ababab这三列加上看成单独的特征即可。
# encoding:utf-8
import numpy as np
import matplotlib.pyplot as plt
# 输入数据(加入偏置和非线性项)
X = np.array([[1,0,0,0,0,0],
[1,0,1,0,0,1],
[1,1,0,1,0,0],
[1,1,1,1,1,1]])
Y = np.array([-1,1,1,-1])
# 初始化权值
W = (np.random.random(6)-0.5)*2
# 学习率、迭代次数、输出临时变量
lr = 0.1
n = 0
O = 0
# 权值的更新函数
def update():
global X,Y,W,lr,n
n+=1
O = np.dot(X,W)
W_C = lr*(X.T.dot(Y-O))/int(X.shape[0])
W = W + W_C
for i in range (1000):
update()
# 正样本
x1=[0,1]
y1=[1,0]
# 负样本
x2=[0,1]
y2=[0,1]
# 二次方程w0+w1*x1+w2*x2+w3*x1*x1+w4*x1*x2+w5*x2*x2=0已知w和x1求x2
def calculate(x,root):
a = W[5]
b = W[2] + x*W[4]
c = W[0] + x*W[1] + x*x*W[3]
if root==1:
return (-b+np.sqrt(b*b-4*a*c))/(2*a)
if root==2:
return (-b-np.sqrt(b*b-4*a*c))/(2*a)
xdata = np.linspace(-1,2)
# 画图
plt.scatter(x1,y1,c='b')
plt.scatter(x2,y2,c='g')
plt.plot(xdata,calculate(xdata,1),'r')
plt.plot(xdata,calculate(xdata,2),'r')
plt.show()
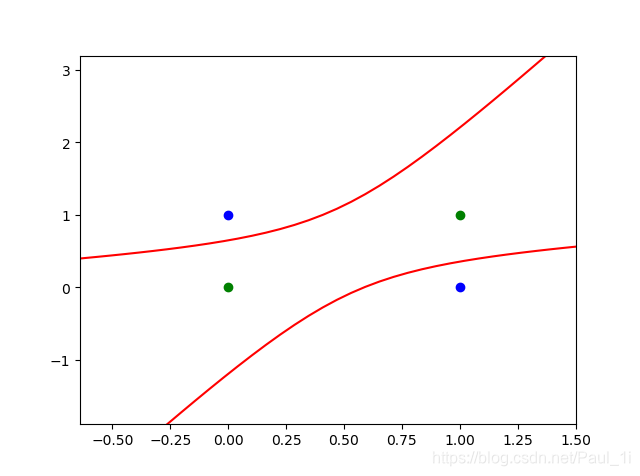








 本文深入探讨了线性神经网络的概念,对比感知机,解释了为何改变激活函数为purelin函数y=x,以及如何通过最小化代价函数进行权值迭代。并通过δ学习规则详细展示了线性神经网络的异或问题解决方案。
本文深入探讨了线性神经网络的概念,对比感知机,解释了为何改变激活函数为purelin函数y=x,以及如何通过最小化代价函数进行权值迭代。并通过δ学习规则详细展示了线性神经网络的异或问题解决方案。
















 2156
2156

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








