主席树（可持久化线段树）学习笔记

（集训的第一个内容）

-------------------

想必各位巨佬早已学习过线段树

主席树是它的一个升级版 可以频繁地支持 连续询问区间第K大这样的操作 

( 就比如 https://www.luogu.org/problemnew/show/P3834 )

我们先把这个问题简单化 考虑先解决询问[1,r]中第k大的数

（为了方便 我们先给一个序列a 1 2 3 5 5 7 7 8）

整理一下a 变为1*1,2*1,3*1,5*2,7*2,8*1  ->1,2,3,5,7,8

再建立数组t t[1]=1,t[2]=2,t[3]=3,t[4]=5,t[5]=7,t[6]=8;

于是就可以通过t建这样一棵树

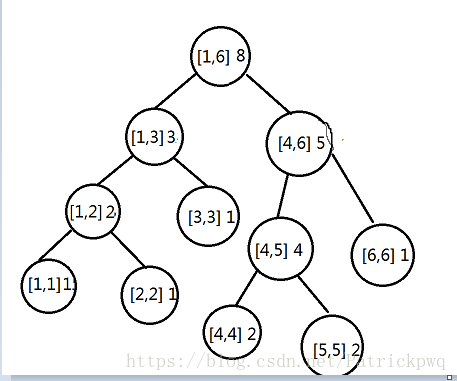
其中，每个节点的区间（l,r）是已经离散化过的数组(即t)的下标 权值代表这个区间出现过的次数

这样就很方便找了 比如要找第5大的数

-----进入根节点，发现5>3，于是走向右儿子，此时相当于要在右儿子找第二大的

-----发现2<=4，走向左儿子

-----发现1<=2，走向左儿子

此时到了叶子节点了，发现当前区间为[4,4]，即对应的是5，所以第五大的就是5

----------------------

以上就是如何查[1,r]中第k大的过程，那么求[l,r]中的第k大呢？

考虑对于每个前缀，我们都建一颗线段树,即1~i,1~i+1,....,1~n，

我们发现 要寻找l~r的排名k 只需要用r这颗线段树减去l-1这颗线段树 每个节点余下的差值象征着l~r之间插入的数 于是这个排名就很好找了 具体理解可以自己配合着代码yy图

但是这样空间复杂度是极其高 要建很多线段树的 轻松就MLE了

考虑优化 

我们发现从1~i到1~i+1有太多重复的地方 1~i+1与1~i的不同相当于只是插了一个数而已 

在建1~i+1这棵树时 如果遇到与1~i重复的地方 就直接把新节点指向1~i的对应点 大概是这样一个意思

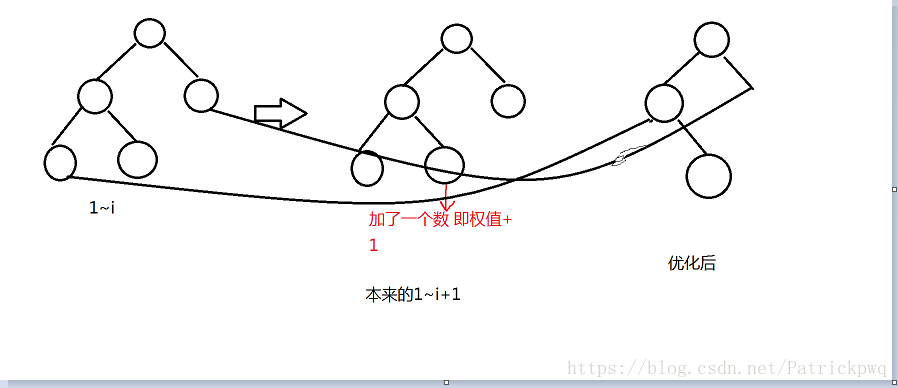
具体实现 请看代码

#include<bits/stdc++.h>
using namespace std;
int L[200005<<5],R[200005<<5],sum[200005<<5];
int a[1000005],b[1000005],t[1000005];
int n,m,q,cnt;
int build(int l,int r)
{
	int rt=++cnt;	//编号持续更新 
	int mid=(l+r)/2;
	if(l<r)
	{
		L[rt]=build(l,mid);	//更新左儿子的编号 
		R[rt]=build(mid+1,r);	//右儿子的编号 
	}	
	return rt;	
}
int update(int cor,int l,int r,int k)	//cor代表对应点(i-1树) l,r是区间 k是排名 
{
	int rt=++cnt;	//编号继续更新 
	L[rt]=L[cor];R[rt]=R[cor];sum[rt]=sum[cor]+1;	//先继承i-1这颗树对应点的信息 但是不同的是sum要+1 
	int mid=(l+r)/2;
	if(l<r)
	{
		if(k<=mid)	L[rt]=update(L[cor],l,mid,k);	//若排名在左边 更新左边  
		else R[rt]=update(R[cor],mid+1,r,k);
	}
	return rt;
}
int query(int last,int now,int l,int r,int k)
{
	if(l==r)	return l;
	int mid=(l+r)>>1;
	int x=sum[L[now]]-sum[L[last]];	//找左儿子的差值 判断这个 
	if(x>=k)	return query(L[last],L[now],l,mid,k);
	else return query(R[last],R[now],mid+1,r,k-x);
}
int main()
{
	cin>>n>>q;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		b[i]=a[i];
	}
	sort(b+1,b+n+1);
	m=unique(b+1,b+n+1)-(b+1);
	t[0]=build(1,m);	//先建一颗空树(根节点是0) 后头要用 
	for(int i=1;i<=n;i++)
	{
		int k=lower_bound(b+1,b+m+1,a[i])-b;
		t[i]=update(t[i-1],1,m,k);
	}
	for(int i=1;i<=q;i++)
	{
		int x,y,k;
		scanf("%d%d%d",&x,&y,&k);
		printf("%d\n",b[query(t[x-1],t[y],1,m,k)]);
	} 
	return 0;
}

主席树基本讲解到此----------