最短路---Dijkstra&Floyd

还是老样子，先上图，说明思想和过程再上代码详细的分步解释

算法图解

今天就不手撸画图了，看到了一个很详尽并且很规整的图，直接拿来用。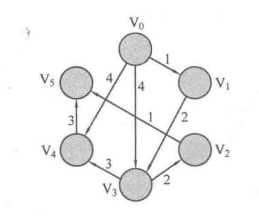
在这个有向图中有6个顶点V0-V5。关于图的内容就不多说了背景故事也懒得编了就来说说这个图用Dijkstra的遍历过程吧。

首先大家要明白Dijkstra的目的是为了解决单源最短路的问题也就是一个起点到各个点的最短路。

在上图中，我们默认起点是V0点，我们希望每次从V0(起点)到达任意一个点的距离尽可能的短，即从起点到达其他点的距离都是最短距离。

Dijkstra是怎么做的呢？

1. 将图中所有的边都抹去
2. 在图中Vi(0≤i≤5)上记录从起点V0到达该城市Vi所需的最短距离

如图进行1步骤对图进行初始化，自己到自己的距离为0

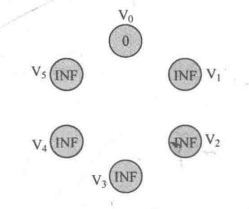
下面再说每次执行的策略：

1. 还未访问过的点Vk选择距离V0最近的访问
2. 到达Vk后，开放链接所有Vk能到达的边，以Vk为中介点，看能否使起点到达其他的距离变短，如果能就更新起点到其他未达点的距离

下面的图会具体展示上述过程:
![在这里插入图片描述](https://img-blog.csdnimg.cn/20200307182823623.png

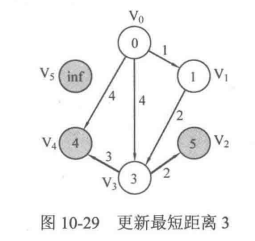
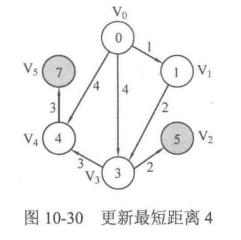
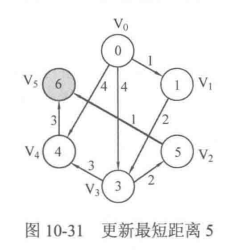
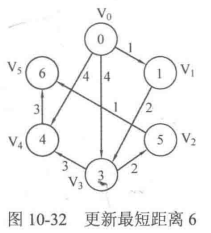
相信大家通过上述的过程图已经很清晰的理解了这个算法到底是干什么的了

那就贴代码再来看看好了

算法核心代码

Dijkstra

#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;

const int INF = 0xffffff;
const int MAXV = 1000;

int m,s,n,G[MAXV][MAXV];//n为顶点数，G为图,m为边数,s为起点
int d[MAXV];//起点到各个点的最短路径长度
bool vis[MAXV] = {false};//初始化访问数组

void Dijkstra(int s){
	fill(d,d+MAXV,INF);//初始化d数组为INF
	d[s] = 0;
	for(int i=0;i<n;i++){
		int u = -1,MIN = INF;
		for(int j = 0;j<n;j++){
			if(vis[j] == false&&d[j]<MIN){
				u = j;
				MIN = d[j];
			}
		}
		//如果没找到说明顶点和起点s不连通
		if(u==-1){
			return ;
		}
		vis[u] = true;
		for (int v = 0;v<n;v++){
			/*如果点可达并且改点没有被访问过,
			并且uv点距离+起点到u点距离<起点到v点距离,
			更新长度*/
			if(vis[v] == false && G[u][v]!=INF && d[u] + G[u][v] < d[v]){
				d[v] = d[u] + G[u][v];
			}
		}
	}
}


int main(){ 
	int x,y,len;
	scanf("%d %d %d",&n,&m,&s);
	fill(G[0],G[0]+MAXV*MAXV,INF);
	for(int i = 0;i<m;i++){
		scanf("%d %d %d",&x,&y,&len);
		G[x][y] = len;
	}
	Dijkstra(s);
	for(int i = 0;i<n;i++){
		printf("%d ",d[i]);
	}
	return 0;
}

Floyd

#include <iostream>
#include<cstdio>
#include<algorithm>

using namespace std;

const int INF = 0xffffff;//不可达的距离
const int MAXV = 200;//最大顶点数

int n,m;//n为顶点数,m为边数

int dis[MAXV][MAXV];//dis[i][j]表示顶点i到j的距离

void Floyd(){
	for(int k = 0;k<n;k++){
		for(int i = 0;i<n;i++){
			for(int j = 0;j<n;j++){
				if(dis[i][k]!=INF&&dis[k][j]!=INF&&dis[i][k]+dis[k][j]<dis[i][j]){
					dis[i][j] = dis[i][k]+dis[k][j];
				}
			}
		}
	}
}

int main(){

	int x,y,len;
	fill(dis[0],dis[0]+MAXV*MAXV,INF);
	scanf("%d %d",&n,&m);
	for (int i = 0; i < n; i++){
		dis[i][i] = 0;
	}
	for(int i = 0;i<m;i++){
		scanf("%d %d %d",&x,&y,&len);
		dis[x][y] = len;
	}
	Floyd();
	for(int i = 0;i<n;i++){
		for(int j = 0;j<n;j++){
			printf("%d ",dis[i][j]);
		}
		printf("\n");
	}
	return 0;
}

过程思想借助了《算法笔记》一书