埃拉托斯特尼筛法

简介：埃拉托斯特尼筛法（Sieve of Eratosthenes）是一种高效计算素数的算法，它能够找出小于等于某个整数 nnn 的所有素数。该算法的基本思想是通过不断筛选合数（非素数）来获取素数，从而避免了对每个数逐一检查是否为素数的过程。

例：

#include <iostream>
using namespace std;

// 计算 1 到 a 之间的素数个数
int Yanhongyan(int a)
{
    bool b[a + 1]; // 布尔数组，用来标记是否为素数
    for (int i = 0; i <= a; i++)
    {
        b[i] = true; // 假设所有数是素数
    }
    b[0] = b[1] = false; // 0 和 1 不是素数

    // 埃拉托斯特尼筛法
    for (int i = 2; i * i <= a; i++)
    {
        if (b[i])
        {
            for (int j = i * i; j <= a; j += i)
            {
                b[j] = false; // 标记 i 的倍数为非素数
            }
        }
    }

    // 统计素数的个数
    int sum = 0;
    for (int i = 2; i <= a; i++)
    {
        if (b[i])
        {
            sum++; // 如果是素数，计数加一
        }
    }

    return sum; // 返回素数个数
}

int main()
{
    int t;
    cin >> t; // 输入测试用例的个数

    // 对每个输入的值输出其对应的素数个数
    while (t--)
    {
        int n;
        cin >> n;                      // 输入每个测试用例的值
        cout << Yanhongyan(n) << endl; // 输出对应的素数个数
    }

    return 0;
}

 

输入为：4
              5
              10
              20
              100

运行结果：

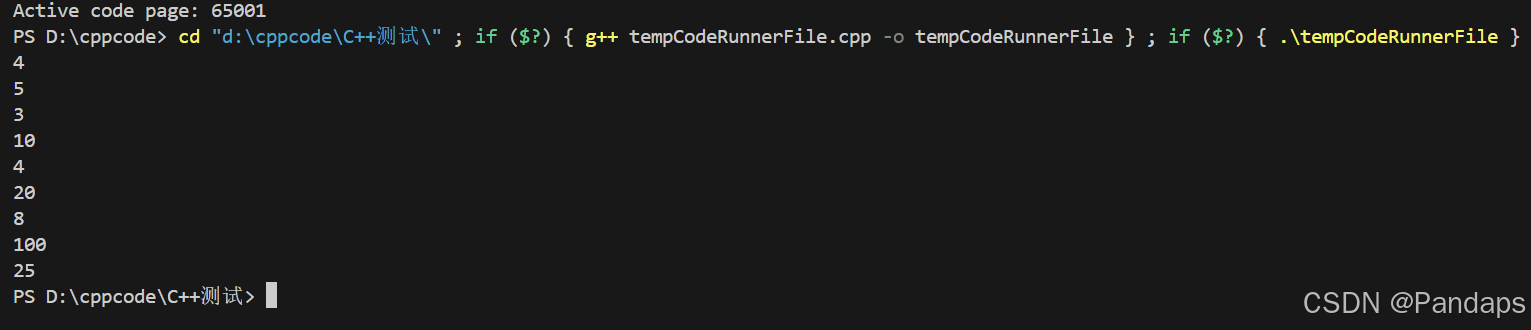
算法步骤：

1. 初始化：创建一个布尔数组 isPrime，其中 isPrime[i] 表示数字 i 是否为素数。将数组中所有元素初始化为 true，并将 isPrime[0] 和 isPrime[1] 设置为 false（因为 0 和 1 不是素数）。
2. 筛选过程：
   • 从 2 开始，检查每个数字。如果该数字是素数，则将它的所有倍数标记为非素数（false）。
   • 从 2 开始标记所有倍数为 false，继续到平方根范围的数字。因为对于任何一个大于 sqrt(n) 的素数，它的倍数都会在之前被处理过。
3. 输出结果：
   • 最终，isPrime[i] 为 true 的位置表示 i 是素数。