6.1
import networkx as nx
import pylab as plt
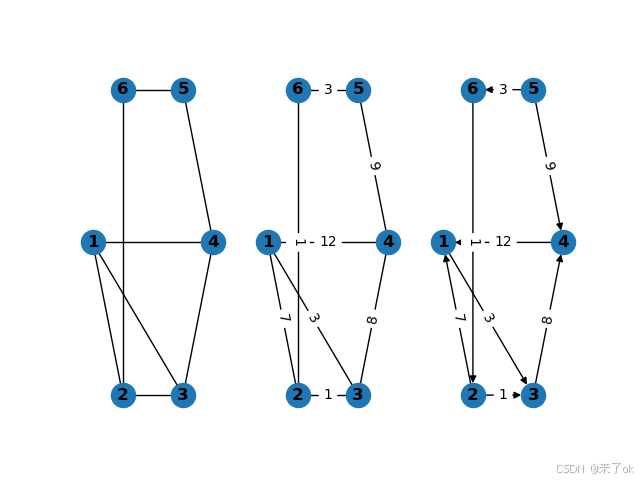
L1=[(1,2),(1,3),(1,4),(2,3),(2,6),(3,4),(4,5),(5,6)]
G1=nx.Graph(); G1.add_nodes_from(range(1,7))
G1.add_edges_from(L1); pos1=nx.shell_layout(G1)
plt.subplot(131)
nx.draw(G1,pos1,with_labels=True,font_weight='bold')
L2=[(1,2,7),(1,3,3),(1,4,12),(2,3,1),(2,6,1),(3,4,8),(4,5,9),(5,6,3)]
G2=nx.Graph(); G2.add_nodes_from(range(1,7))
G2.add_weighted_edges_from(L2); pos2=nx.shell_layout(G2)
plt.subplot(132)
nx.draw(G2,pos2,with_labels=True,font_weight='bold')
w2=nx.get_edge_attributes(G2,'weight')
nx.draw_networkx_edge_labels(G2,pos2,edge_labels=w2)
L3=[(1,3,3),(2,1,7),(2,3,1),(3,4,8),(4,1,12),(5,4,9),(5,6,3),(6,2,1)]
G3=nx.DiGraph(); G3.add_nodes_from(range(1,7))
G3.add_weighted_edges_from(L3); pos3=nx.shell_layout(G3)
plt.subplot(133)
nx.draw(G3,pos3,with_labels=True,font_weight='bold')
w3=nx.get_edge_attributes(G3,'weight')
nx.draw_networkx_edge_labels(G3,pos3,edge_labels=w3)
plt.show()
6.2
edges = [
("Pe", "T", 13),
("Pe", "N", 68),
("Pe", "M", 78),
("Pe", "L", 51),
("Pe", "Pa", 51),
("T", "N", 68),
("T", "M", 70),
("T", "L", 60),
("T", "Pa", 61),
("N", "M", 21),
("N", "L", 35),
("N", "Pa",36),
("M", "L", 56),
("M", "Pa", 57),
("L", "Pa", 21),
]
class UnionFind:
def __init__(self, n):
self.parent = list(range(n))
self.rank = [0] * n
def find(self, u):
if self.parent[u] != u:
self.parent[u] = self.find(self.parent[u])
return self.parent[u]
def union(self, u, v):
root_u = self.find(u)
root_v = self.find(v)
if root_u != root_v:
if self.rank[root_u] > self.rank[root_v]:
self.parent[root_v] = root_u
elif self.rank[root_u] < self.rank[root_v]:
self.parent[root_u] = root_v
else:
self.parent[root_v] = root_u
self.rank[root_u] += 1
def kruskal(edges):
edges.sort(key=lambda edge: edge[2])
uf = UnionFind(len(set(city for edge in edges for city in edge[:2])))
mst = []
for u, v, weight in edges:
if uf.find(u) != uf.find(v):
uf.union(u, v)
mst.append((u, v, weight))
return mst
city_map = {
"Pe": 0, "T": 1, "N": 2, "M": 3, "L": 4, "Pa": 5
}
edges_with_indices = [(city_map[u], city_map[v], weight) for u, v, weight in edges]
mst_edges = [(list(city_map.keys())[u], list(city_map.keys())[v], weight) for u, v, weight in kruskal(edges_with_indices)]
print("最小生成树的边:")
for u, v, weight in mst_edges:
print(f"{u} - {v}: {weight}")

6.3
import heapq
def prim(graph, start):
num_nodes = len(graph)
visited = [False] * num_nodes
min_heap = [(0, start, -1)]
mst_cost = 0
mst_edges = []
while min_heap:
weight, u, parent = heapq.heappop(min_heap)
if visited[u]:
continue
visited[u] = True
mst_cost += weight
if parent != -1:
mst_edges.append((parent, u, weight))
for v in range(num_nodes):
if not visited[v] and graph[u][v] != 0:
heapq.heappush(min_heap, (graph[u][v], v, u))
return mst_cost, mst_edges
graph = [
[0,20,0,0,15,0],
[20,0,20,60,25,0],
[0,20,0,30,18,0],
[0,60,30,0,35,10],
[0,0,0,10,15,0]
]
mst_cost, mst_edges = prim(graph, 0)
print("Prim's MST Cost:", mst_cost)
print("Prim's MST Edges:", mst_edges)
 6.4
6.4
initial_costs = [2.5, 2.6, 2.8, 3.1]
salvage_values = [2.0, 1.6, 1.3, 1.1]
maintenance_costs = [0.3, 0.8, 1.5, 2.0]
dp = [[float('inf')] * 2 for _ in range(4)]
dp[0][1] = initial_costs[0] + maintenance_costs[0]
for i in range(1, 4):
dp[i][1] = min(dp[i-1][1] + maintenance_costs[i],
initial_costs[i] + maintenance_costs[i])
if i > 0:
dp[i][0] = dp[i-1][1] + salvage_values[i-1]
min_cost = min(dp[3][1],
min(dp[i][0] for i in range(3)))
print(f"最优更新策略下的4年内最小总费用为:{min_cost}万元")
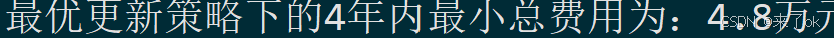 6.5
6.5
import numpy as np
distances = np.array([
[0, 2, 7, np.inf, np.inf, np.inf],
[2, 0, 4, 6, 8, np.inf],
[7, 4, 0, 1, 3, np.inf],
[np.inf, 6, 1, 0, 1, 6],
[np.inf, 8, 3, 1, 0, 3],
[np.inf, np.inf, np.inf, 6, 3, 0]
], dtype=float)
students = np.array([50, 40, 60, 20, 70, 90])
hospital_distances_sum = np.zeros(6)
for i in range(6):
connected_distances = distances[i, :i+1].copy()
connected_distances = connected_distances[connected_distances != np.inf]
hospital_distances_sum[i] = np.sum(connected_distances)
hospital_location = np.argmin(hospital_distances_sum)
print(f"医院应该建在村庄 {chr(65 + hospital_location)} 处,使得最远村庄的人到医院看病所走的路最短。")
school_total_distances = np.zeros(6)
for i in range(6):
weighted_distances = 0
for j in range(6):
if distances[j, i] != np.inf:
weighted_distances += students[j] * distances[j, i]
school_total_distances[i] = weighted_distances
school_location = np.argmin(school_total_distances)
print(f"小学应该建在村庄 {chr(65 + school_location)} 处,使得所有学生上学走的总路程最短。")

6.6
import numpy as np
matches = np.array([
[0, 1, 0, 1, 1, 1], # 1队
[0, 0, 0, 1, 1, 1], # 2队
[1, 1, 0, 1, 0, 0], # 3队
[0, 0, 0, 0, 1, 1], # 4队
[0, 0, 1, 0, 0, 1], # 5队
[0, 0, 1, 0, 0, 0] # 6队
], dtype=int)
n = matches.shape[0]
closure = matches.copy()
for k in range(n):
for i in range(n):
for j in range(n):
closure[i, j] = closure[i, j] or (closure[i, k] and closure[k, j])
strength = closure.sum(axis=1)
ranking = np.argsort(-strength)
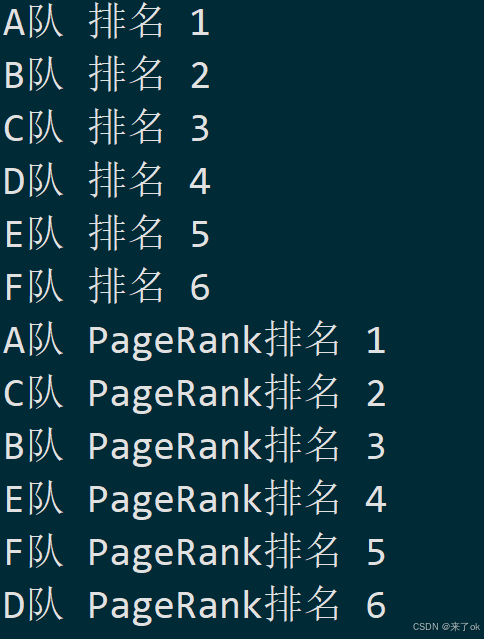
for i, rank in enumerate(ranking):
print(f"{chr(65 + rank)}队 排名 {i + 1}")
import numpy as np
from scipy.sparse import csr_matrix
edges = [
(0, 1), (0, 3), (0, 4), (0, 5), # 1队胜
(1, 3), (1, 4), (1, 5), # 2队胜
(2, 0), (2, 1), (2, 3), # 3队胜
(3, 4), (3, 5), # 4队胜
(4, 2), (4, 5), # 5队胜
(5, 2) # 6队胜
]
num_teams = 6
row_ind = []
col_ind = []
data = []
for u, v in edges:
row_ind.append(u)
col_ind.append(v)
data.append(1)
adj_matrix = csr_matrix((data, (row_ind, col_ind)), shape=(num_teams, num_teams))
adj_matrix_T = adj_matrix.T
d = 0.85
out_degree = np.array(adj_matrix_T.sum(axis=1)).flatten()
out_degree[out_degree == 0] = 1
M = adj_matrix_T.multiply(1.0 / out_degree).tocsr()
M = M + (1 - d) / num_teams * csr_matrix(np.ones((num_teams, num_teams)))
R = np.ones(num_teams) / num_teams
num_iterations = 100
for _ in range(num_iterations):
R = R.dot(M.toarray())
pagerank_ranking = np.argsort(-R)
for i, rank in enumerate(pagerank_ranking):
print(f"{chr(65 + rank)}队 PageRank排名 {i + 1}")





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








