算法之‘备忘录‘思想

    好的代码往往需要程序员不断的优化，代码的优化目的就是 ：降低时间复杂度和空间复杂度。

    在动态规划中，由于会运用到数学归纳法的思想（通过子问题的答案推出大问题的答案)，我们常常使用递归的方式来解决此类问题。但在递归过程中常常会重复求出子问题的答案，这是很浪费时间的，所以我们可以考虑能否用数组来暂时储存这些计算得到的数据方便后续的调用以此来减少运行时长。

为了增加对比效果，这里直接上代码：

代码例题为 ：兔子数组（1，1，2，3，5......）

1. 未带备忘录的代码实现

#include<stdio.h>

int Fib(int);

int main()
{
	int number, i;
	printf("请输入数组的长度:");
	scanf("%d", &number);
	for(i=1; i<=number; i++){
		printf("%d ", Fib(i));
        if(i%20==0){
			printf("\n");
		}
	}
	return 0;
}

int Fib(int num)
{
	if(num==1||num==2){
		return 1;
	}else{
		return Fib(num - 2) + Fib(num - 1);
	}
}

输出数组长度为30的运行时间为：6.332S

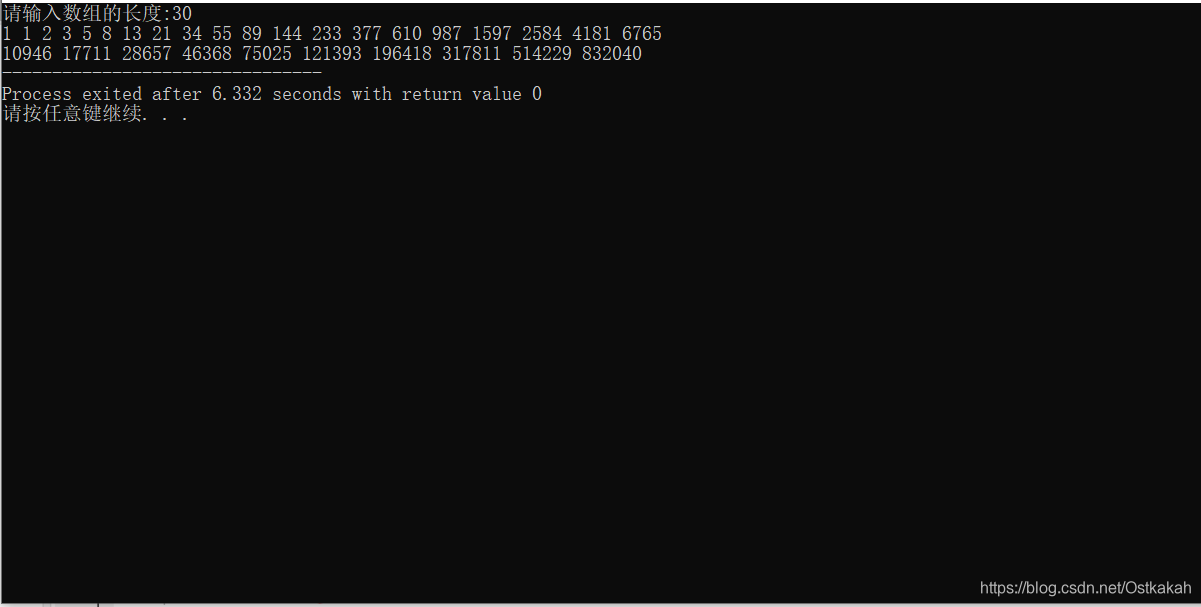
2.带备忘录的代码实现

#include<stdio.h>

int Fib(int, int *);

int main()
{
	int number, i;
	printf("请输入数组的长度:");
	scanf("%d", &number);
	int data[number + 1];//data为备忘录数组;
	for(i = 1;i<=number;i++){//data初始化;
		data[i] = 0;
	}
	for(i = 1;i<=number;i++){
		printf("%d ", Fib(i, data));
		if(i%20==0){
			printf("\n");
		}
	}
	return 0;
}

int Fib(int num, int *data)
{
	if(num==1||num==2){
		data[num] = 1;
	}else{
		if(data[num - 2]==0){//判断之前是否有运算过;
			Fib(num - 2, data);
		}
		if(data[num - 1]==0){
			Fib(num - 1, data);
		}
		data[num] = data[num - 2] + data[num - 1];
	}
	return data[num];
}

输出数组长度为30的运行时间为： 5.909S

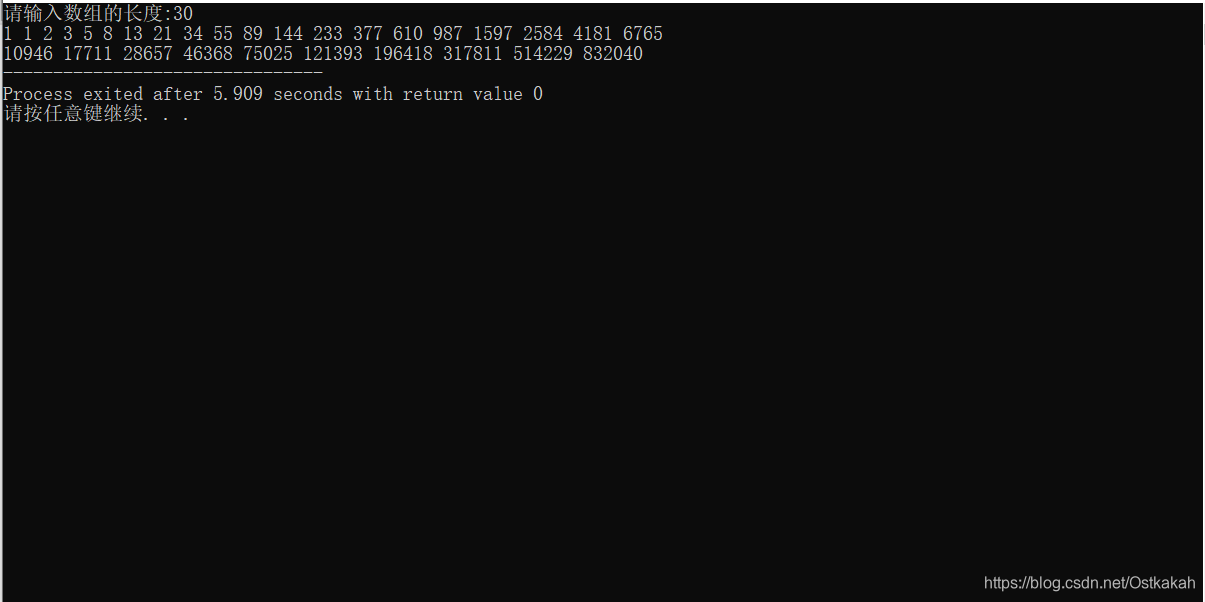
    从两者的运行时间可以看出带有‘备忘录’的代码运行速度更快。这里的运行效果可能还不够明显，如果读者时间充裕的话，可以尝试输出50个，到时候的运行时间差就会很大。

---

总结

1.构建‘备忘录’的思想常常用在动态规划上，加快整体运行速度。

2.‘备忘录’的实质是以空间换时间。

3.在数据量较大的才推荐使用‘备忘录’, 因为数据量较小时‘备忘录’对运行速度的影响不是很明显，反而会浪费空间。