【数据结构】并查集（leetcode-547.朋友圈）

最新推荐文章于 2025-01-14 11:48:00 发布

原创最新推荐文章于 2025-01-14 11:48:00 发布 · 998 阅读

3 ·

CC 4.0 BY-SA版权

数据结构专栏收录该内容

8 篇文章

订阅专栏

博客围绕求解学生朋友圈总数展开。给定表示学生朋友关系的二维矩阵，通过将问题简化到一维数组求解。创建数组并初始化，遍历二维数组调整一维数组，利用并查集的特性，最终以数组中元素为负的个数确定朋友圈数量，还提及合并时的注意事项。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目描述

班上有 N 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。

给定一个 N * N 的矩阵 M，表示班级中学生之间的朋友关系。如果M[i][j] = 1，表示已知第 i 个和 j 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/friend-circles

案例分析

假设存在以下10名同学，朋友圈q1={0,6,7,8}，朋友圈q2={1,4,9}，朋友圈q3={2,3,5}，用下面的森林来表示他们之间的关系
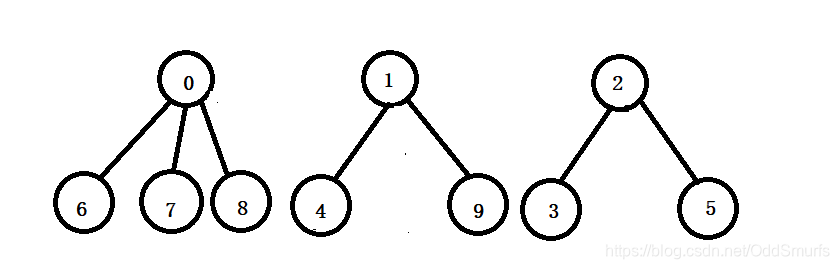
在这里插入图片描述
当然以上的根节点不做要求，只要是在一个朋友圈中的任意一个都可以作为根，这里为了方便实现，将号码小的作为根
而如何来实现在给定的二维数组里面找出朋友圈的数量？

为了简化这个问题，我们不妨在一维数据里面进行求解：
第一步、创建大小为学生数的数组，并初始化为-1
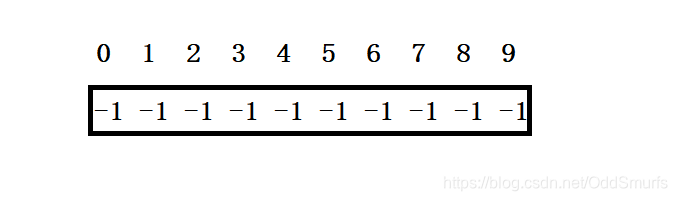
在这里插入图片描述
由于朋友圈的关系是一个无向图，也就意味着我跟你是朋友，同样你跟我也是朋友，然后遍历上面的二维数组，只要对应的数字为1表示彼此就是朋友，然后再下面的一位数组里面进行调整：0和6是朋友，将一位数组中下标为6的数字加等到为0的下标上，然后置该元素为下标0
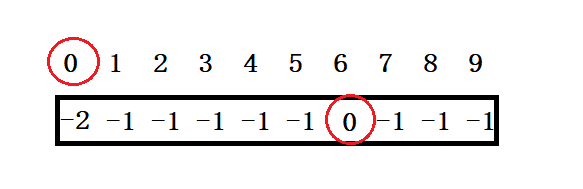
在这里插入图片描述
在遍历二维数组的过程中跟定会有半数的元素需要重复考虑，在代码实现的时候只需要进行条件判断是否已经在一个朋友圈中了就可以避免，经过调整，最后的数组如下

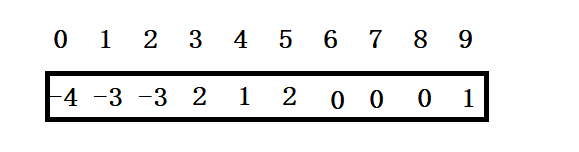
可以发现，调整过后一位数组中元素为负的个数即是朋友圈的数量
而这个一维数组就是所谓的并查集

将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-ﬁnd set)

它一般能解决：

查找元素属于哪个集合沿着数组表示树形关系以上一直找到根(即：树中中元素为负数的位置)
查看两个元素是否属于同一个集合沿着数组表示的树形关系往上一直找到树的根，如果根相同表明在同一个集合，否则不在
将两个集合归并成一个集合将两个集合中的元素合并将一个集合名称改成另一个集合的名称
集合的个数遍历数组，数组中元素为负数的个数即为集合的个数。

代码实现

并查集

在合并的时候需要注意，合并两个朋友圈内的人建立联系，不过两个人不是根节点，要分别找到根节点，再进行合并

class UnionFindSet {
    int[] arr;
    int size;

    public UnionFindSet(int size) {
        this.arr = new int[size];
        for (int i = 0; i<size; i++){
            arr[i] = -1;
        }
        this.size = size;
    }
    //寻找父节点，没有就返回自己
    public int find(int x){
        while (arr[x] >= 0){
            x = arr[x];
        }
        return x;
    }
    public boolean isInSameSet(int a, int b){
        return find(a) == find(b);
    }
    //合并的时候先找根节点
    public void union(int a, int b){
        int rootA = find(a);
        int rootB = find(b);
        arr[rootA] += arr[rootB];
        arr[rootB] = rootA;
    }
    public int getSize(){
        int count = 0;
        for (int i : arr){
            if (i < 0){
                count++;
            }
        }
        return count;
    }
}

如果上面的3和8成为了朋友
则森林变成如下状态
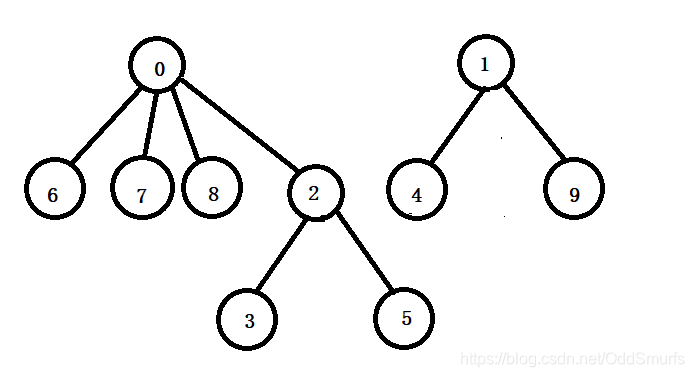
在这里插入图片描述
一维数组变成如下状态

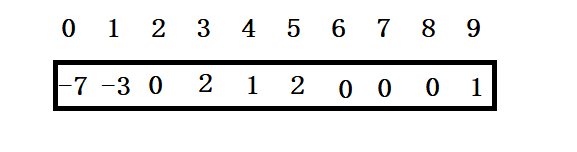
问题解决

在合并的时候进行判断，如果两个同学已经在同一个朋友圈中，则不再进行合并

public class Solution {
    public static int findCircleNum(int[][] M) {
        int n = M.length;
        UnionFindSet ufs = new UnionFindSet(n);
        for (int i = 0; i<n; i++){
            for (int j = 0; j<n; j++){
                if (M[i][j] == 1 && !ufs.isInSameSet(i, j)){
                    ufs.union(i, j);
                }
            }
        }
        return ufs.getSize();
    }
}