hdu 4686 Arc of Dream 矩阵快速幂-优快云博客

本文介绍了一种利用矩阵快速幂方法求解特定形式的线性递推序列问题的技术。通过构造适当的转移矩阵并应用快速幂运算，可以在对数时间内高效计算出递推序列的第n项。

a₀ = A0
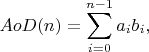
a_i = a_i-1*AX+AY
b₀ = B0

b_i = b_i-1*BX+BY

//****************************

以上是条件：推得：

Sn = Sn-1 + an*bn;

an*bn = Ax*Bx * an-1 * bn-1 + Bx*Ay *bn-1 + Ax*By*ai-1 + Ay*By

分析得：

an*bn 可以由 an-1*bn-1 , bn-1 , an-1 通过先行关系求的。

bn ,an 可有 bn-1 an-1 通过线性关系求的。

所以 Sn 可以有线性关系求的。手动构造出转移矩阵。快速幂求解。

#include <vector>
#include <list>
#include <map>
#include <set>
#include <deque>
#include <stack>
#include <cstring>
#include <bitset>
#include <algorithm>
#include <functional>
#include <numeric>
#include <utility>
#include <sstream>
#include <iostream>
#include <iomanip>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <ctime>
#include <assert.h>
#include <queue>
#define REP(i,n) for(int i=0;i<n;i++)
#define TR(i,x) for(typeof(x.begin()) i=x.begin();i!=x.end();i++)
#define ALLL(x) x.begin(),x.end()
#define SORT(x) sort(ALLL(x))
#define CLEAR(x) memset(x,0,sizeof(x))
#define FILLL(x,c) memset(x,c,sizeof(x))
using namespace std;
const double eps = 1e-9;
#define LL long long 
#define pb push_back
const int  maxn = 5;
const int size = 5;
const LL MOD = 1000000007;
LL A0,AX,AY;
LL B0,BX,BY;
LL n;
struct Mat{
    long long mat[maxn][maxn];
    void init(){
         memset(mat,0,sizeof(mat));
         mat[0][0] = 1;
         mat[1][0] = 1;
         mat[1][1] = AX*BX%MOD;
         mat[2][1] = AX*BY%MOD; mat[2][2] = AX;
         mat[3][1] = AY*BX%MOD;                 mat[3][3] = BX;
         mat[4][1] = AY*BY%MOD; mat[4][2] = AY; mat[4][3] = BY; mat[4][4] = 1;
    }
    void show(){
        for(int i=0;i<=4;i++){
            for(int j=0;j<=4;j++){
                 cout << mat[i][j]<< " ";
            }
            cout <<endl;
        }
    }
    LL get_ans(){
        return A0*B0%MOD*mat[1][0] %MOD + A0*mat[2][0]%MOD+ B0*mat[3][0]%MOD + mat[4][0];
    }
}E,g;
void init_E(){
   memset(E.mat,0,sizeof(E.mat));
   for(int i=0;i<size ;i++){
      E.mat[i][i] =1 ;
   }
}
Mat operator*(const Mat &a,const Mat &b){
    Mat c;
    for(int i=0;i<size;i++)
        for(int j=0;j<size;j++){
            c.mat[i][j] = 0;
            for(int k=0;k<size;k++){
                if(a.mat[i][k] && b.mat[k][j])
                    c.mat[i][j]=(c.mat[i][j]+a.mat[i][k]*b.mat[k][j]%MOD)%MOD;
            }
            
        }
    return c;
}

Mat operator^(Mat a,LL x){
    Mat c=E;
    for(;x;x>>=1){
        if(x&1)
            c=c*a;
        a=a*a;
    }
    return c;
}
Mat pow2(Mat a,LL x){
    Mat c = E;
    while(x){
        if(x&1){
            c = c*a;
        }
        a= a*a;
        x= x>>1;
    }
    return c;
}
void solve(){
    g.init();
    g = pow2(g,n);
    LL ans = g.get_ans();
    ans %= MOD;
    cout << ans<<endl;
}
int main(){
    init_E();
    while(~scanf("%I64d",&n)){
        scanf("%I64d%I64d%I64d",&A0,&AX,&AY);
        scanf("%I64d%I64d%I64d",&B0,&BX,&BY);
        solve();
    }
    return 0;
}