BF，KMP，BM算法以及完整代码

BF，KMP，BM算法详解

1.实验题目

给定一个文本，在该文本中查找并定位任意给定字符串。

2.实验目的

1.深刻理解并掌握蛮力法思想。

2.提高蛮力法设计算法的技能。

3.理解这样一个观点：用蛮力法设计的算法，一般来说，经过适度的努力后，都可以对算法的第一个版本进行一定程度的改良，改进其时间性能。

3.实验要求

实现BF、KMP算法，实现BM算法

4.算法思想与核心代码

（1）BF算法

BF算法其实思路相对简单，总的来说，就是模式串与主串“一对一”匹配，如果匹配失败，子串回溯到头部，并且从模式串的下一个元素开始与子串头匹配。时间复杂度较高，为O（m*n），m为模式串长度，n为主串长度，以下都是。

BF代码

//BF
int BF(const char s[],const char t[])
{
   
   
    int index=0;
    int i=0,j=0;
    while(s[i]!='\0'&&t[j]!='\0')
    {
   
   
        if(s[i]==t[j])
        {
   
      i++;
            j++;}
        else
        {
   
   index++,i=index,j=0;}
    }
    if(t[j]=='\0')
        return index+1;//不是下标
    else
        return index;
}

（2）KMP算法

KMP算法是相对于BF算法的改进，改进点主要是在主串的遍历上，主串只需遍历一遍，算法的精髓在于求最长相等的前后缀。

首先，需要理解几个概念：

通过举例说明：

字符串 abcdab
前缀的集合：{a,ab,abc,abcd,abcda}
后缀的集合：{b,ab,dab,cdab,bcdab}
最长相等的前后缀：ab

abcabfabcab中最长相等前后缀：abcab

KMP算法就是将已经匹配的串中，找到相等的前缀和后缀，然后将前缀移动到后缀的位置上，如下图：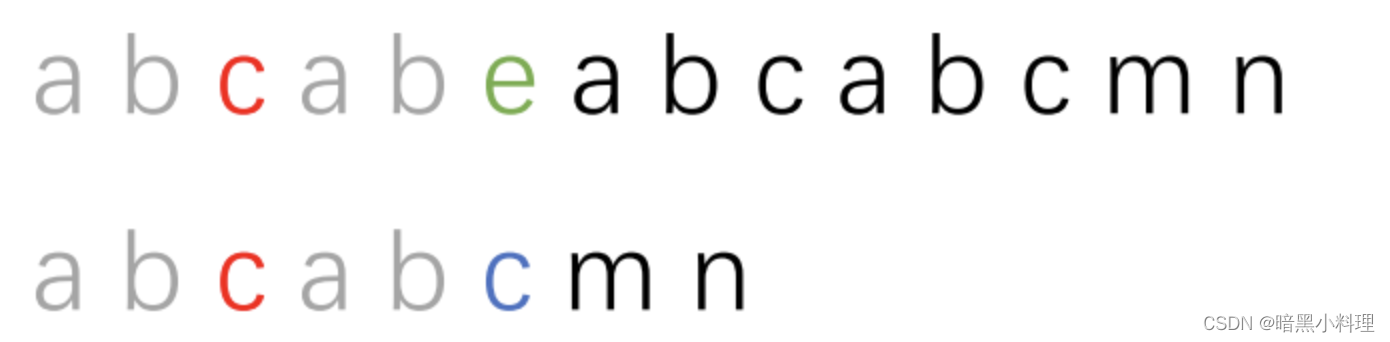

匹配，发现e和c不相等，比较“abcab”中的前后缀，发现有最长相等的前后缀“ab“，直接移动到如下图所示位置：

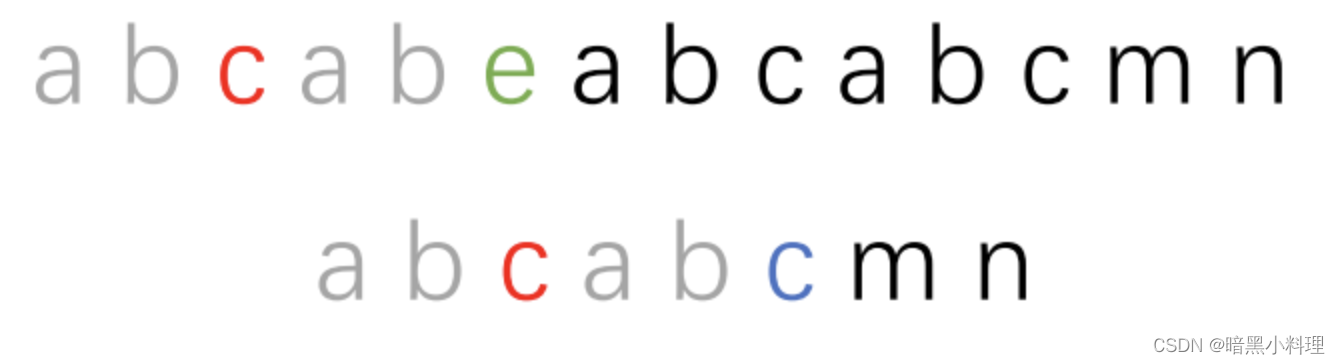
那么我们怎么求最长相等前后缀呢？

用一个next数组来求，next[i]表示前i个元素中最长相等前后缀的长度，若值为-1，则表示不可能出现最长相等前后缀。

例：我们用“ababc"这个字符串来求这个next数组：

当i=0时，因为前0个里面甚至连元素都没有，所以next[0]=-1;

当i=1时，前一个元素无最长相等前后缀，所以next[1]=0;

当i=2时，前两个元素为ab，无最长相等前后缀，next[2]=0;

当i=3时，前三个元素为aba，发现有最长相等前后缀，为“a”，且为一个，则next[3]=1;

当i=4时，前四个元素为abab，发现有最长相等前后嘴，为“ab”，且为两个，则next[4]=2;
注意，最后一个元素不计入next数组的计算范围内。

此时，next数组求解完毕。

求解next数组的代码

//next
void GetNext(int next[],const char t[])//t为模式串
{
   
   
    int i,j,len;
    next[0]=-1;
    for(j=1;t[j]!='\0';j++)
    {
   
   
        for(len=j-