参考:
https://baike.baidu.com/item/%E5%8D%A1%E7%89%B9%E5%85%B0%E6%95%B0/6125746
公式: C ( m , n ) = n ! m ! ∗ m ! C(m,n) = \frac{n!}{m!*m!} C(m,n)=m!∗m!n! 、 A ( m , n ) = n ! m ! A(m,n) = \frac{n!}{m!} A(m,n)=m!n!
卡特兰数
1.定义及推导
卡特兰数Cn满足以下递推关系 [1] :
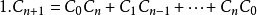
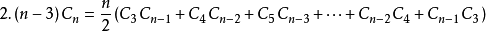
设h(n)为catalan数的第n+1项,令h(0)=1,h(1)=1,catalan数满足递推式
h
(
n
)
=
h
(
0
)
∗
h
(
n
−
1
)
+
h
(
1
)
∗
h
(
n
−
2
)
+
.
.
.
+
h
(
n
−
1
)
∗
h
(
0
)
(
n
>
=
2
)
h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)*h(0) (n>=2)
h(n)=h(0)∗h(n−1)+h(1)∗h(n−2)+...+h(n−1)∗h(0)(n>=2)
例如:
h
(
2
)
=
h
(
0
)
∗
h
(
1
)
+
h
(
1
)
∗
h
(
0
)
=
1
∗
1
+
1
∗
1
=
2
h(2)=h(0)*h(1)+h(1)*h(0)=1*1+1*1=2
h(2)=h(0)∗h(1)+h(1)∗h(0)=1∗1+1∗1=2
h
(
3
)
=
h
(
0
)
∗
h
(
2
)
+
h
(
1
)
∗
h
(
1
)
+
h
(
2
)
∗
h
(
0
)
=
1
∗
2
+
1
∗
1
+
2
∗
1
=
5
h(3)=h(0)*h(2)+h(1)*h(1)+h(2)*h(0)=1*2+1*1+2*1=5
h(3)=h(0)∗h(2)+h(1)∗h(1)+h(2)∗h(0)=1∗2+1∗1+2∗1=5
另类递推式:
h
(
n
)
=
h
(
n
−
1
)
∗
(
4
∗
n
−
2
)
/
(
n
+
1
)
;
h(n)=h(n-1)*(4*n-2)/(n+1);
h(n)=h(n−1)∗(4∗n−2)/(n+1);
递推关系的解为:
h
(
n
)
=
C
(
n
,
2
n
)
/
(
n
+
1
)
(
n
=
0
,
1
,
2
,
.
.
.
)
h(n)=C(n,2n)/(n+1) (n=0,1,2,...)
h(n)=C(n,2n)/(n+1)(n=0,1,2,...)
递推关系的另类解为:
h
(
n
)
=
c
(
n
,
2
n
)
−
c
(
n
−
1
,
2
n
)
(
n
=
0
,
1
,
2
,
.
.
.
)
h(n)=c(n,2n)-c(n-1,2n)(n=0,1,2,...)
h(n)=c(n,2n)−c(n−1,2n)(n=0,1,2,...)
证明
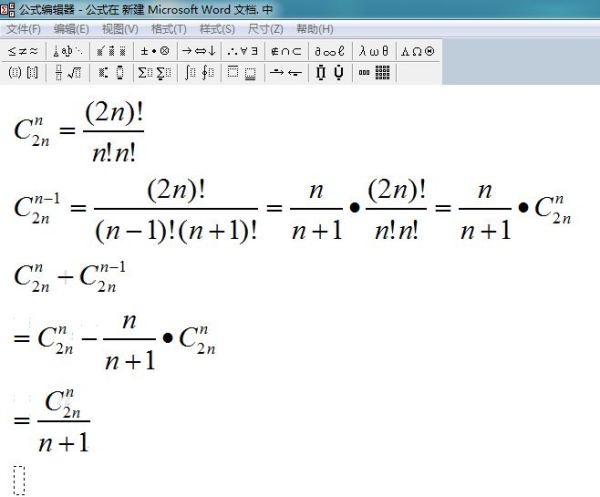
折纸法推导:折纸法推导

2.应用
一个栈(无穷大)的进栈序列为1,2,3,…,n,有多少个不同的出栈序列?
常规分析
首先,我们设f(n)=序列个数为n的出栈序列种数。(我们假定,最后出栈的元素为k,显然,k取不同值时的情况是相互独立的,也就是求出每种k最后出栈的情况数后可用加法原则,由于k最后出栈,因此,在k入栈之前,比k小的值均出栈,此处情况有f(k-1)种,而之后比k大的值入栈,且都在k之前出栈,因此有f(n-k)种方式,由于比k小和比k大的值入栈出栈情况是相互独立的,此处可用乘法原则,f(n-k)*f(k-1)种,求和便是Catalan递归式。
首次出空之前第一个出栈的序数k将1n的序列分成两个序列,其中一个是1k-1,序列个数为k-1,另外一个是k+1~n,序列个数是n-k。
此时,我们若把k视为确定一个序数,那么根据乘法原理,f(n)的问题就等价于——序列个数为k-1的出栈序列种数乘以序列个数为n - k的出栈序列种数,即选择k这个序数的f(n)=f(k-1)×f(n-k)。而k可以选1到n,所以再根据加法原理,将k取不同值的序列种数相加,得到的总序列种数为:f(n)=f(0)f(n-1)+f(1)f(n-2)+……+f(n-1)f(0)。
看到此处,再看看卡特兰数的递推式,答案不言而喻,即为f(n)=h(n)= C(2n,n)/(n+1)= c(2n,n)-c(2n,n-1)(n=0,1,2,……)。
非常规分析
对于每一个数来说,必须进栈一次、出栈一次。我们把进栈设为状态‘1’,出栈设为状态‘0’。n个数的所有状态对应n个1和n个0组成的2n位二进制数。由于等待入栈的操作数按照1‥n的顺序排列、入栈的操作数b大于等于出栈的操作数a(a≤b),因此输出序列的总数目=由左而右扫描由n个1和n个0组成的2n位二进制数,1的累计数不小于0的累计数的方案种数。
在2n位二进制数中填入n个1的方案数为c(2n,n),不填1的其余n位自动填0。从中减去不符合要求(由左而右扫描,0的累计数大于1的累计数)的方案数即为所求。
不符合要求的数的特征是由左而右扫描时,必然在某一奇数位2m+1位上首先出现m+1个0的累计数和m个1的累计数,此后的2(n-m)-1位上有n-m个 1和n-m-1个0。如若把后面这2(n-m)-1位上的0和1互换,使之成为n-m个0和n-m-1个1,结果得1个由n+1个0和n-1个1组成的2n位数,即一个不合要求的数对应于一个由n+1个0和n-1个1组成的排列。
反过来,任何一个由n+1个0和n-1个1组成的2n位二进制数,由于0的个数多2个,2n为偶数,故必在某一个奇数位上出现0的累计数超过1的累计数。同样在后面部分0和1互换,使之成为由n个0和n个1组成的2n位数,即n+1个0和n-1个1组成的2n位数必对应一个不符合要求的数。
因而不合要求的2n位数与n+1个0,n-1个1组成的排列一一对应。
显然,不符合要求的方案数为c(2n,n+1)。由此得出输出序列的总数目=c(2n,n)-c(2n,n-1)=c(2n,n)/(n+1)=h(n)。
类似问题 买票找零
有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票,另外n人只有10元钞票,剧院无其它钞票,问有多少种方法使得只要有10元的人买票,售票处就有5元的钞票找零?(将持5元者到达视作将5元入栈,持10元者到达视作使栈中某5元出栈)
凸多边形三角划分
在一个凸多边形中,通过若干条互不相交的对角线,把这个多边形划分成了若干个三角形。任务是键盘上输入凸多边形的边数n,求不同划分的方案数f(n)。比如当n=6时,f(6)=14。
分析
如果纯粹从f(4)=2,f(5)=5,f(6)=14,……,f(n)=n慢慢去归纳,恐怕很难找到问题的递推式,我们必须从一般情况出发去找规律。
因为凸多边形的任意一条边必定属于某一个三角形,所以我们以某一条边为基准,以这条边的两个顶点为起点P1和终点Pn(P即Point),将该凸多边形的顶点依序标记为P1、P2、……、Pn,再在该凸多边形中找任意一个不属于这两个点的顶点Pk(2<=k<=n-1),来构成一个三角形,用这个三角形把一个凸多边形划分成两个凸多边形,其中一个凸多边形,是由P1,P2,……,Pk构成的凸k边形(顶点数即是边数),另一个凸多边形,是由Pk,Pk+1,……,Pn构成的凸n-k+1边形。
此时,我们若把Pk视为确定一点,那么根据乘法原理,f(n)的问题就等价于——凸k多边形的划分方案数乘以凸n-k+1多边形的划分方案数,即选择Pk这个顶点的f(n)=f(k)×f(n-k+1)。而k可以选2到n-1,所以再根据加法原理,将k取不同值的划分方案相加,得到的总方案数为:f(n)=f(2)f(n-2+1)+f(3)f(n-3+1)+……+f(n-1)f(2)。看到此处,再看看卡特兰数的递推式,答案不言而喻,即为f(n)=h(n-2) (n=2,3,4,……)。
最后,令f(2)=1,f(3)=1。
此处f(2)=1和f(3)=1的具体缘由须参考详尽的“卡特兰数”,也许可从凸四边形f(4)=f(2)f(3)+ f(3)f(2)=2×f(2)f(3)倒推,四边形的划分方案不用规律推导都可以知道是2,那么2×f(2)f(3)=2,则f(2)f(3)=1,又f(2)和f(3)若存在的话一定是整数,则f(2)=1,f(3)=1。(因为我没研究过卡特兰数的由来,此处仅作刘抟羽的臆测)。





















 5210
5210

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








