LeetCode刷题-数组463：岛屿的周长

题目

给定一个 row x col 的二维网格地图 grid ，其中：grid[i][j] = 1 表示陆地， grid[i][j] = 0 表示水域。

网格中的格子 水平和垂直 方向相连（对角线方向不相连）。整个网格被水完全包围，但其中恰好有一个岛屿（或者说，一个或多个表示陆地的格子相连组成的岛屿）。

岛屿中没有“湖”（“湖” 指水域在岛屿内部且不和岛屿周围的水相连）。格子是边长为 1 的正方形。网格为长方形，且宽度和高度均不超过 100 。计算这个岛屿的周长。

示例1：

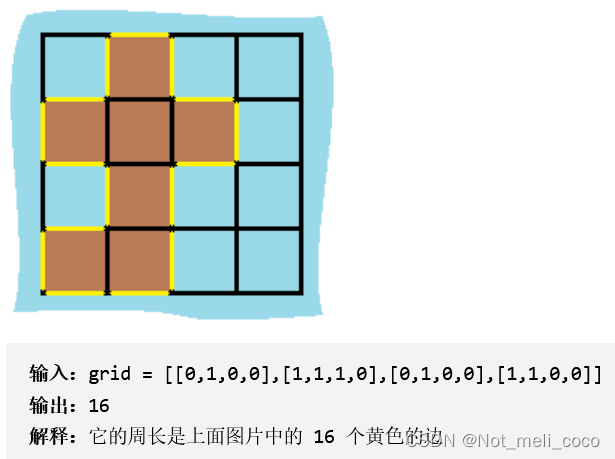
示例2：

输入：grid = [[1]]
输出：4

示例3：

输入：grid = [[1,0]]
输出：4

提示：

row == grid.length
col == grid[i].length
1 <= row, col <= 100
grid[i][j] 为 0 或 1

解题思路

看到这个问题，首先想到的是遍历每一个格子，当遇到陆地时（grid[i][j]==1），判断其四周是否与水域相邻，有几个方向与水域相邻，周长就加几。这种方法需要注意在网格最外圈（边界）比较特殊，比如第一个格子grid[0][0]，与其相邻的只有右和下，这些特殊的格子需要分情况判断，这么一想有些麻烦。那要是换个思路呢~

法一：（执行用时：100ms，内存消耗：13.1MB）

        还是对网格进行遍历，每遇到一个格子是陆地就让周长加4，然后判断只要在它前面或者上面有陆地相邻，那就减2。因为当方格A与方格B相邻时，方格A、B有一条边重合了，那么在计算周长时，它们需要各减少一条边。

        这种方法同样适用于陆地有湖和有多个陆地等情况。

class Solution(object):
    def islandPerimeter(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        c = 0
        if not grid or len(grid) == 0:
            return 0
        for i in range(0,len(grid)):
            for j in range(0,len(grid[i])):
                if grid[i][j] == 1:
                    c += 4
                if i>0 and grid[i-1][j]==1:
                    c -= 2
                if j>0 and grid[i][j-1]==1:
                    c -= 2
        return c

法二：容斥原理（执行用时：108ms，内存消耗：13MB）

其实跟前面的方法是类似的

如果被计数的事物有 AA、BB、CC 三类，那么，AA 类和 BB 类和 CC 类元素个数总和 == AA 类元素个数 ++ BB 类元素个数++ CC 类元素个数 —— 既是 AA 类又是 BB 类的元素个数 —— 既是 AA 类又是 CC 类的元素个数 —— 既是 BB 类又是 CC 类的元素个数 ++ 既是 AA 类又是 BB 类而且是 CC 类的元素个数。(A∪B∪C=A+B+C−A∩B−B∩C−C∩A+A∩B∩C)(A∪B∪C=A+B+C−A∩B−B∩C−C∩A+A∩B∩C)

根据题目，如果考虑只有两个格子相交（A和B），根据容斥原理，它们各自的周长是4，既属于A又属于B的边数有2条，因此8-2 = 6

 

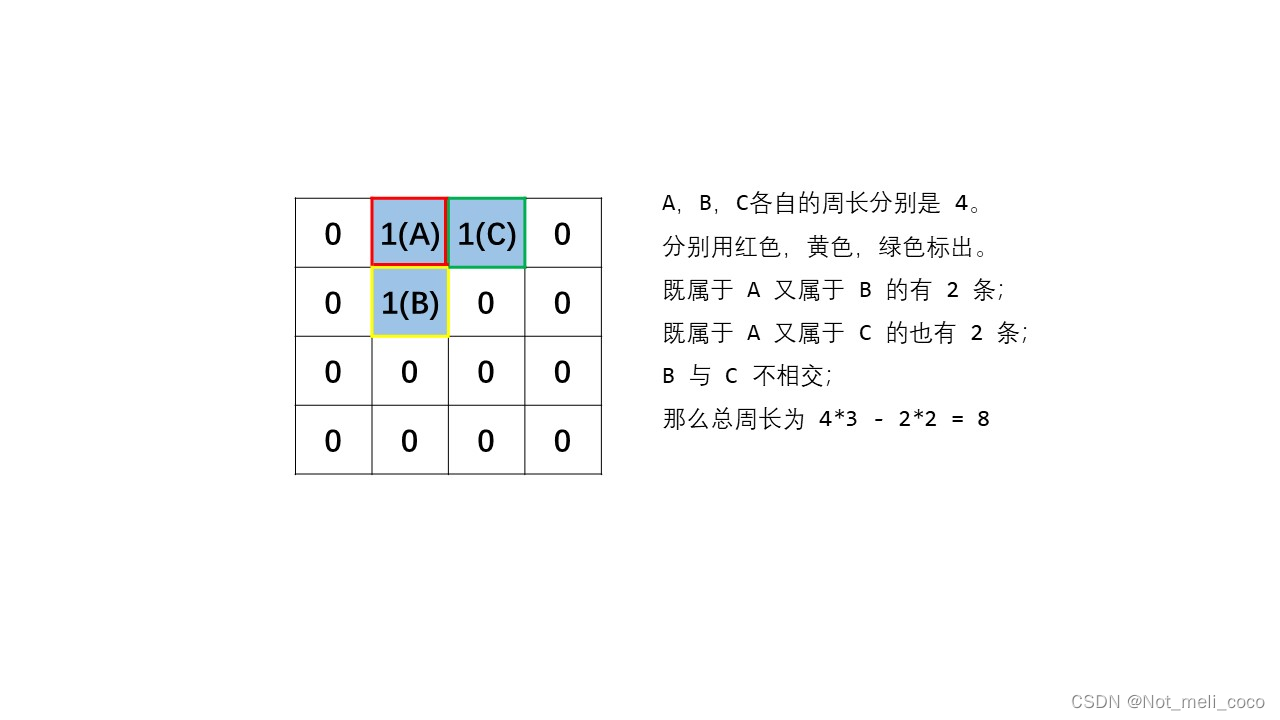
再来看三个格子相交的情况，假设叫做陆地 AA，陆地 BB，陆地 CC，根据容斥原理，它们各自的周长分别是 44，既属于 AA 又属于 BB 的有 22 条，既属于 AA 又属于 CC 的也有 22 条，BB 与 CC 不相交，那么总周长为 4∗3−2∗2=84∗3−2∗2=8

 以此可以推广到更多的格子相交，因此，我们在遍历到每个点的时候，只需要对其下方或者右边判断是否有格子即可。

以上解释摘自

作者：HarmonJiangMLE
链接：https://leetcode.cn/problems/island-perimeter/solution/hdu5538xiang-tong-si-lu-rong-chi-yuan-li-jie-ti-by/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

 

class Solution(object):
    def islandPerimeter(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        if not grid:
            return 0
        c = 0
        for i in range(0,len(grid)):
            for j in range(0,len(grid[i])):
                if grid[i][j] == 1:
                    if i<len(grid)-1 and grid[i+1][j]==1:
                        down = 2
                    else:
                        down = 0
                    if j<len(grid[i])-1 and grid[i][j+1]==1:
                        right = 2
                    else:
                        right = 0
                    c += 4-down-right
        return c

时间复杂度：O(mn)，其中m，n分别是grid的行与列数

空间复杂度：O(1)