Codeforces 1838 F Stuck Conveyor 解析

题目地址

https://codeforces.com/problemset/problem/1838/F

题目抽象

本题是一道交互题
在一个 $n\ast n$ 的传送带矩阵中，你可以控制所有传输带的传送方向（上下左右 ^ v < >）
不过有一个传输带坏掉了，只能固定某个方向，无法调整
需要你在 $25$ 次询问(交互)内，找到坏掉的传送带

每次交互，可以你做如下询问：
将一个箱子放在指定的某一个传送带上，并设置各个传送带的方向

每次询问，系统会给出如下答案：
将各个传送带设置为你给的方案（坏掉的那个无法设置），然后告诉你箱子最终会落在哪个位置（在 n*n 矩阵之外），如果出现循环，则返回 -1 -1

数据范围：
$1\le n\le 100$

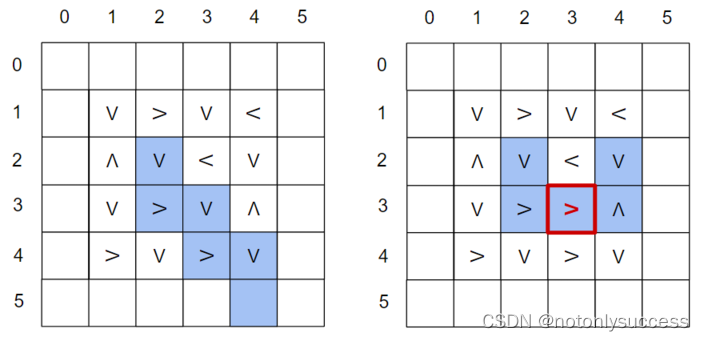
解释：按照下边左图的配置，如果选 (2 2) 作为起点，那么箱子最终落点应该是 (5 4)，但因为 (3 3) 位置的传送带是坏的，只能朝向右边，所以最终会陷入死循环，输出 (-1 -1)

题目类型

构造，二分

解题思路

用尽可能少的询问找到坏掉的传送带
要在 10000 个格子里用 25 次询问找到目标各自，很容易想到二分

思路一

我们将传送带分成两部分，在第一部分中进行探测，如果出现逾期之外的情况，说明坏的传送带在这一部分，另一部分就不需要再询问了，反之亦然。
这样子我们可以通过 $\log n^2$ 次探测就找到，而$n$最大是$100$，所以可以在 $\lceil \log 100^2\rceil =14$次探测就能找到答案

要检测一个区域内是否有坏的传送带，我们需要构造一个传送序列，将箱子放在起点，然后可以经过所有传送带，如果最后的落点不符合预期，则说明坏的传送带在这一块
但如果符合预期呢？我们无法判断坏的传送带是否在此，因为坏的传送带指向可能和我们构造的传送带相同
所以我们需要将重点作为起点，方向再询问一次，如果还符合预期，说明坏的传送带不在这个区域
所以每次探测最快的情况需要2次询问才能确定一个区域
很不幸，用这种方式最坏的情况需要 2 * 14 = 28 次询问才行，超过了 25 次，相差了3次

分析上边的方案，发现有一些无效的询问，如果一个区域正向没问题，反向有问题，那么后续在这个区域内的二分，就没必要探测正向的内容，只需要探测反向就行了
所以每次探测只有 1/4 的概率一次询问就探测出坏传送带（选择坏的传送带所在区域，选择可以探测出坏传送带的方向），经过计算大概会有 97% 左右的概率能将总体询问次数降低到 25 次以内。
我们可以随机区域的左右，随机方向的正方。因为这个概率已经很高了，就算有 50 组极限case，我们期望随机 5 次也能过

思路二

我们将二维的传送带拉成一维（构造一个从一个点出发能遍历完所有传送带的路径），然后从左到右，从右到左分别进行传输，如果某个方向上发现结果不符合预期，说明这个方向的传输可以探测出坏传送带
然后我们以这个为模板，对起点进行二分，最终就能通过 14 次询问找到坏传送带的位置
然后还原回二维，将该位置的上下左右方向的传送带分别设置为^ v < >，以这个传送带作为起点，再进行一次探测，落点的方向就是坏传送带的朝向
这种做法最差情况会在 2 + 14 次询问后确定位置，然后花 1 次询问确定朝向，符合 25 次找到目标的的条件

代码

思路二：

#include <bits/stdc++.h>
using namespace std;

int n;
char mp[101][101];
void gen(bool anti) {
  for (int i = 1; i <= n; i ++) {
    for (int j = 1; j <= n; j ++) {
      if (anti) {
        if (i & 1) {
          mp[i][j] = '<';
          if (i != 1 && j == 1) {
            mp[i][j] = '^';
          }
        } else {
          mp[i][j] = '>';
          if (j == n) {
            mp[i][j] = '^';
          }
        }
      } else {
        if (i & 1) {
          mp[i][j] = '>';
          if (i != n && j == n) {
            mp[i][j] = 'v';
          }
        } else {
          mp[i][j] = '<';
          if (i != n && j == 1) {
            mp[i][j] = 'v';
          }
        }
      }
    }
  }
}
void query(int x, int y) {
  cout << "? " << x << ' ' << y << endl;
  for (int i = 1; i <= n; i ++) {
    for (int j = 1; j <= n; j ++) {
      cout << mp[i][j];
    }
    cout << endl;
  }
  cout << endl;
  cout.flush();
}

bool match(int pos, int ansx, int ansy) {
  int posx = (pos - 1) / n + 1;
  int posy = (posx & 1) ? (pos - 1) % n + 1 : n - (pos - 1) % n;
  query(posx, posy);
  int x, y;
  cin >> x >> y;
  return (x == ansx && y == ansy);
}

void solve() {
  cin >> n;
  // 探测出现问题的方向
  int x, y, ansx = n, ansy = (n & 1) ? n + 1 : 0;
  bool anti = false;
  gen(anti);
  query(1, 1);
  cin >> x >> y;
  if (x == ansx && y == ansy) {
    anti = true;
    gen(anti);
    query(n, (n & 1) ? n : 1);
    ansx = 1, ansy = 0;
    cin >> x >> y;
  }

  // 二分找出现问题的传送带
  int lo = 1;
  int hi = n * n;
  int pos;
  while (lo <= hi) {
    int mid = (lo + hi) >> 1;
    if (match(mid, ansx, ansy)) {
      if (anti) {
        lo = mid + 1;
      } else {
        hi = mid - 1;
      }
    } else {
      pos = mid;
      if (anti) {
        hi = mid - 1;
      } else {
        lo = mid + 1;
      }
    }
  }
  
  // 最后询问确定方向
  int posx = (pos - 1) / n + 1;
  int posy = (posx & 1) ? (pos - 1) % n + 1 : n - (pos - 1) % n;
  for (int i = 1; i <= n; i ++) {
    if (i < posy) mp[posx][i] = '<';
    else mp[posx][i] = '>';
    if (i < posx) mp[i][posy] = '^';
    else mp[i][posy] = 'v';
  }
  query(posx, posy);
  cin >> x >> y;
  char dir;
  if (x == 0) dir = '^';
  else if (x == n + 1) dir = 'v';
  else if (y == 0) dir = '<';
  else dir = '>';
  cout << "! " << posx << ' ' << posy << ' ' << dir << endl;
  cout.flush();
}
int main() {
  solve();
}