| Written by | title | date |
|---|---|---|
| zhengchu1994 | 《A Comprehensive Survey of Graph Embedding:Problems, Techniques and Applications》 | 2018年6月9日09:08:16 |
文章目录
Intro
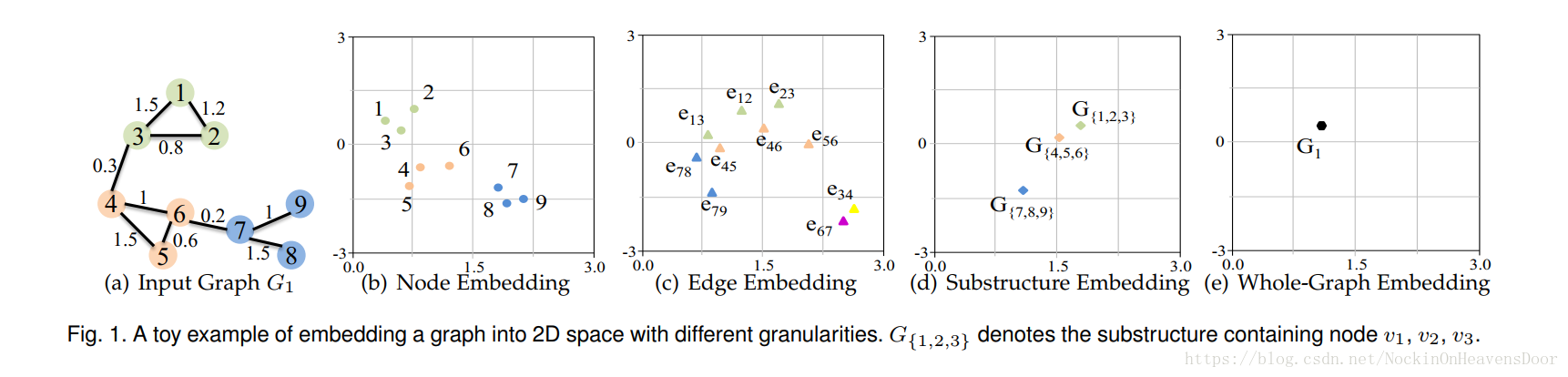
Problem Formalization
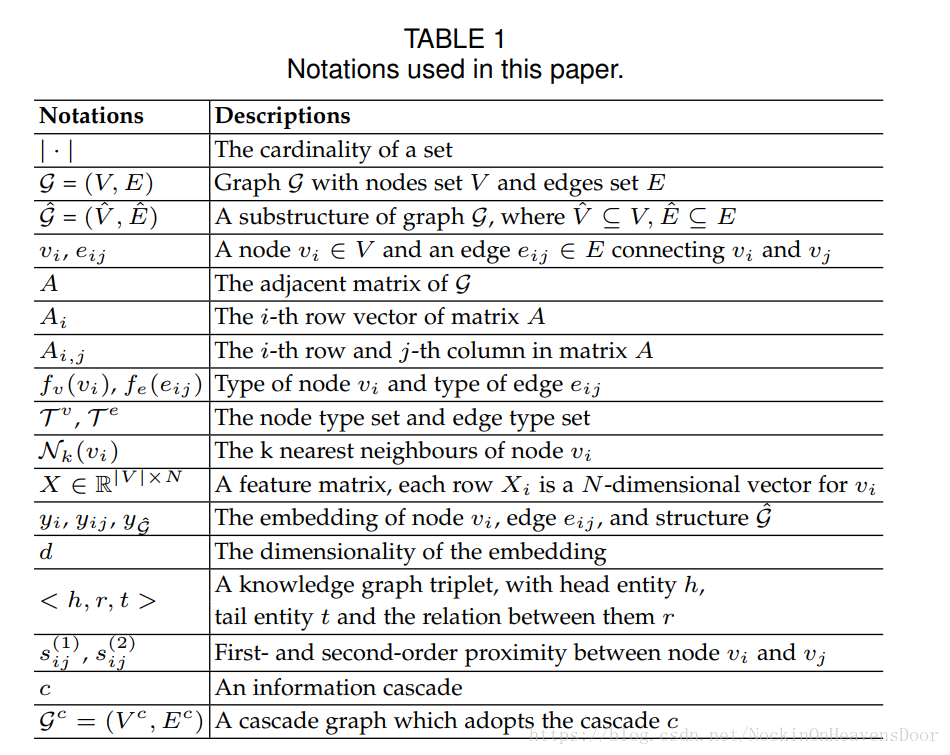
图:
图是 G = ( V , E ) \mathcal G=(V,E) G=(V,E) ,每个 G \mathcal G G 都关联着一个节点类型映射函数 f v : V → T v f_v:V \rightarrow \mathcal T^v fv:V→Tv和边类型映射函数 f v : E → T e f_v:E \rightarrow \mathcal T^e fv:E→Te。其中 T v \mathcal T^v Tv 是节点类型集合, T e \mathcal T^e Te 是边类型集合。
同质图(homogeneous graph):
∣ T v ∣ | \mathcal T^v| ∣Tv∣ =$|\mathcal T^e| =1 $
异构图(heterogeneous graph):
∣ T v ∣ ≥ 1 | \mathcal T^v| \ge 1 ∣Tv∣≥1 and / or $ |\mathcal T^e| \ge 1 $
知识图谱(knowledge graph) :
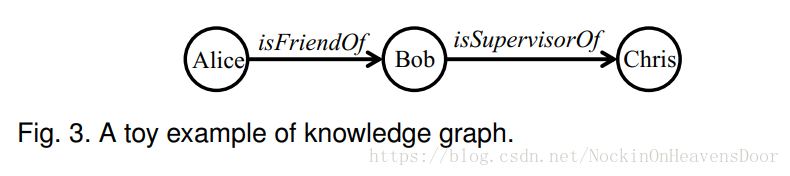
<
h
,
r
,
t
>
<h, r, t>
<h,r,t>,实体和关系都有不同的类型,可以看做异构图的一种例子。
一阶邻近性(first-order proximity):
二阶邻近性(second-order proximity):
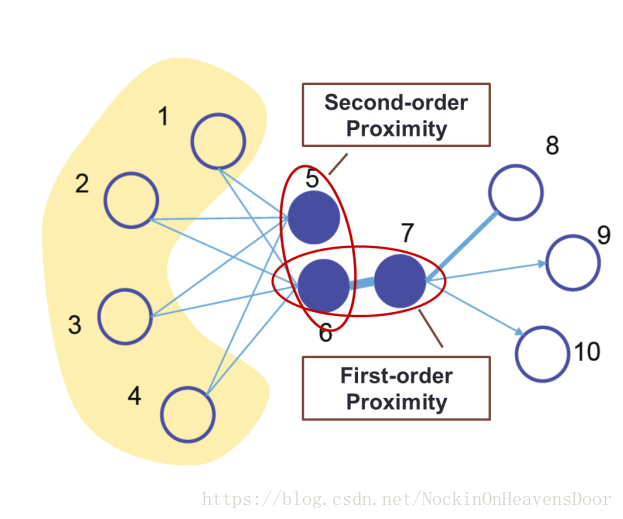
高阶邻近性(high-order proximity):
- 二阶邻近性的推广。
- other metrics:Katz Index,Rooted PageRank,Adamic Adar,etc.
图的嵌入(graph embedding):

Problem Setting Of Graph Embedding
从图嵌入的输入(graph embedding input)和输出(graph embedding output)介绍图嵌入(Graph Embedding),因为大部分图嵌入研究的是每个节点生成一个embedding,所以下面说明图嵌入的输入假设输出为节点的embedding。
graph embedding input
homogeneous graph
进一步分为带权\无权图或者有向\无向图:
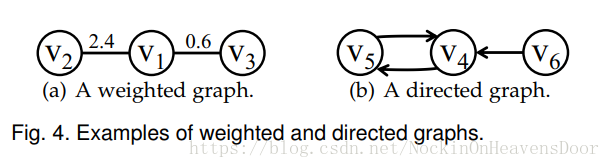
challenge:同质图只有结构信息,所以挑战是用embedding尽可能保留连接模式(connectivity pattern)。
heterogeneous graph
异构图主要存在于下面三个方面:
基于社区的问答网站:
不同类型的节点:问题、答案、用户等,根据利用的边不同区分的表:

多媒体网络:
涵盖多种媒体信息的网络,如图像、文本等多种类别信息。
知识图谱:
例子:从freebase构建的与电影相关的知识图谱,实体类型如**“director”、“actor”、“file”等,关系类型如“produce”,“direct”,“act_in”**等。
其他:
wikipedia、移动数据图等。
challenge:不同类型的对象都嵌入在同一空间,如何在不同类型的对象上得到全局一致性(global consistency),如果不同类型的对象存在偏置,怎么处理?
带有额外信息(auxiliary information)的图
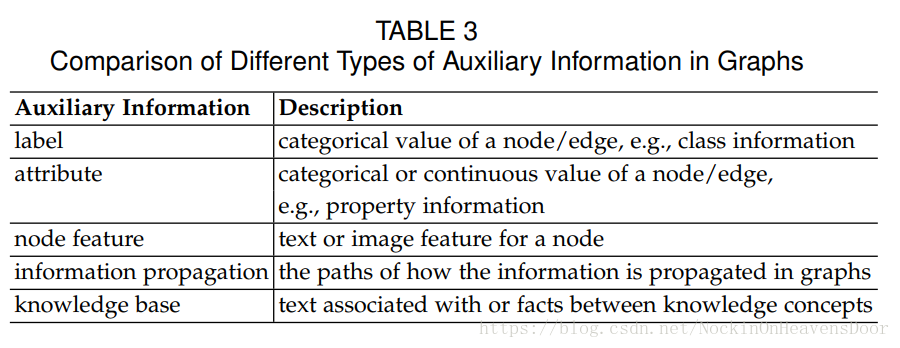
challenge:怎么把丰富的非结构信息与需要保留的拓扑信息一同保留进embedding中。
从关系型数据建立的图
输入是特征矩阵(feature matrix) X ∈ R ∣ V ∣ × N X \in \Bbb R^{| V| \times N} X∈R∣V∣×N ,表示有 V V V 个顶点,特征维度是 N N N;构建用来做图嵌入的相似度矩阵 S S S ,其中 S i j S_{ij} Sij 衡量的是相似性 ( X i , X j ) (X_i,X_j) (Xi,Xj) ,一种是直接用邻接矩阵 A A A 作为 S S S ,一种用节点共现做边的构建,如图像的像素作为节点他们的空间关系来构建边,还有其他的方式,如目标类型、文本信息等构建 S S S。
challenge: 怎么对非关系型数据计算关系。
graph embedding output
图嵌入的输出是有任务驱动的(task driven),因为节点的embedding得到之后常用来做聚类、分类任务,但是并不局限于节点级别,可以对节点对、子图、整个图用来做embedding然后用来做应用需要的任务,所以图嵌入输出的第一个问题便是:为embedding找一个合适的输出类型。
节点嵌入:
近邻节点的输出embedding相似,但是怎么衡量节点间的**“closeness”**,除了一阶、二阶近邻、还有高阶邻近,此外,也有定义同一社区内的节点输出的embedding相似。
challenge: 节点嵌入的最大挑战是如何对不同类型的输入图定义节点间的相似性并在训练过程中保留这种相似性到embedding中。
边嵌入:
目的是得到边的embedding。如知识图谱的embedding都是学习实体和关系的embedding,基于 h h h 和 t t t 学习得到 r r r的embedding,那么就可以在后面预测缺失的实体\关系,做知识图谱的补全。还有如 n o d e 2 v e c node2vec node2vec 在节点的embedding上得到边的embedding,让节点对具有可比性,从而用来预测边的存在。
challenge:挑战是怎么定义边的相似性问题、如果边具有非对称性(asymmetric property)如何建立模型保留(即有向边的性质)?
合成嵌入:
即节点与边的共同embedding,子图的embedding,路径的embedding。
- 对子图做embedding,从而得到图的分类。
- [94]对查询实体到问答实体的路径和子图做embedding
[94] A. Bordes, S. Chopra, and J. Weston, “Question answering with
subgraph embeddings,” in EMNLP, 2014, pp. 615–620.
- 社区做embedding,一个社区嵌入为一个向量。
注:节点嵌入与社区嵌入的互相加入能提高各自的embedding。
challenge: 怎么得到目标子结构(即所需要的embedding做的正是所需要的子结构的embedding而不是不需要的子结构的embedding),因为子结构的嵌入并没有给出其目的是为什么,以及在**同一空间怎么对不同类型的图做embedding。**对embedding的目标类型具有的异构特性怎么做embedding。
全图嵌入:
蛋白质、分子的全图做embedding,有助于图分类、图相似比对等。
challenge: 怎么得到全局意义上的图性质,以及对有效性(得到图的全局性质一般耗时)和表达性做平衡(trade-off)(embedding的有效信息多大)。
#Graph Embedding Techniques
- graph embedding算法的不同之处在于:保留什么样的
graph property,而这由不同的定义来决定。
总览:
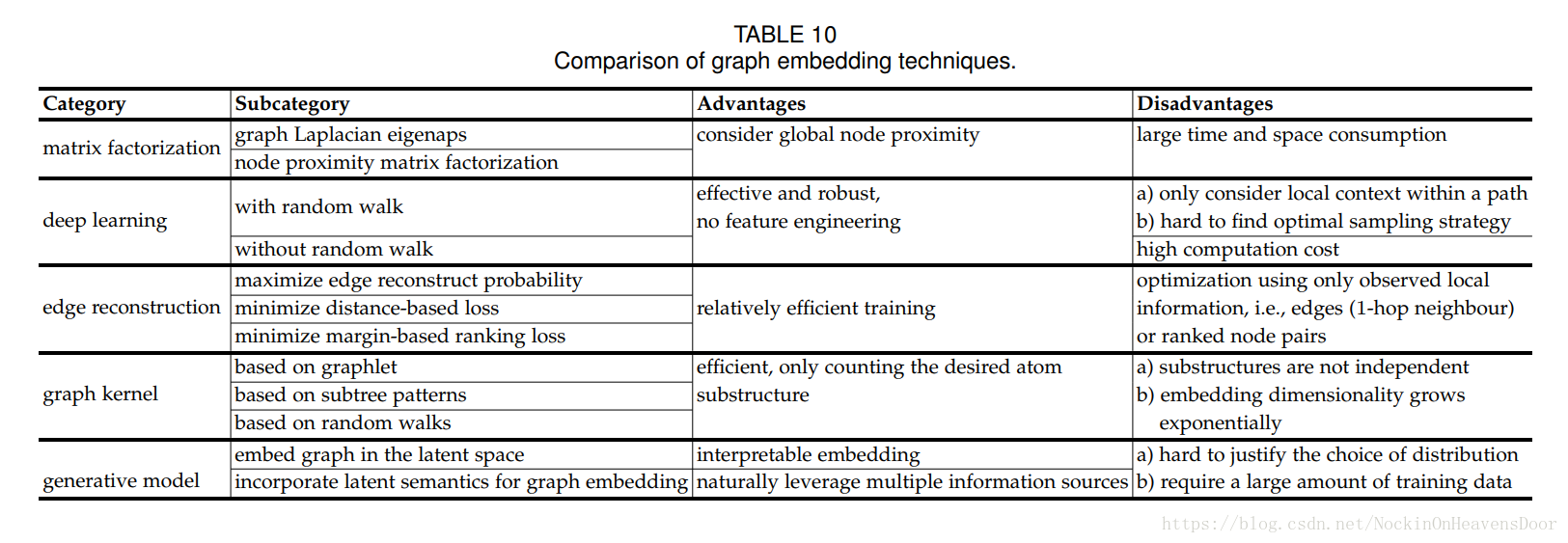
矩阵分解
问题类型:等于保留数据结构的降维,即假设输入数据存在于低维流形。
graph laplacian eigenmaps
Insight: 把graph property定义为成对节点间的相似性,惩罚嵌入之后距离很远但是相似度高的节点。
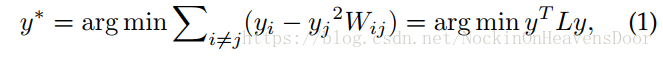
其中:
y
y
y 代表embedding;W代表相似度矩阵,
L
=
D
−
W
L= D - W
L=D−W 是graph Laplacian;D是对称矩阵
D
i
i
=
∑
i
≠
j
W
i
j
D_{ii}=\sum_{i \ne j}W_{ij}
Dii=∑i̸=jWij,看出来
D
i
i
D_{ii}
Dii 越大,节点
i
i
i 和别的节点的相似度越高,说明节点
i
i
i 越重要。(比如连接很多周围节点的中心节点)。
通常还限制
y
T
D
y
=
1
y^TDy=1
yTDy=1 来作为(1)的正则化:

由公式(2)可知
y
y
y 最优的解是
W
y
=
λ
D
y
Wy =\lambda Dy
Wy=λDy 对应最大特征值的特征向量。
还给出了由transductive到inductive的解决方法之一:即给出节点的特征
X
X
X,就能训练新节点的embedding:
y
=
X
T
a
y = X^Ta
y=XTa ,由此(1)变成求
a
a
a 的目标函数:
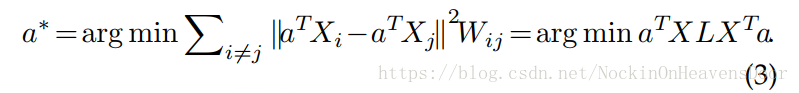
同样加上
a
T
X
L
X
T
a
=
1
a^TXLX^Ta = 1
aTXLXTa=1 的限制:
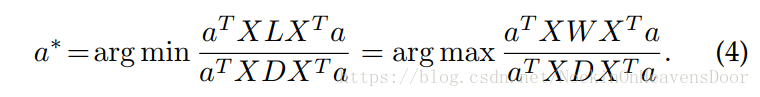
得 a a a 的解是最大特征值对应的特征向量 X W X T a = λ X D X T a XWX^Ta=\lambda XDX^Ta XWXTa=λXDXTa
由此衍生的方法:
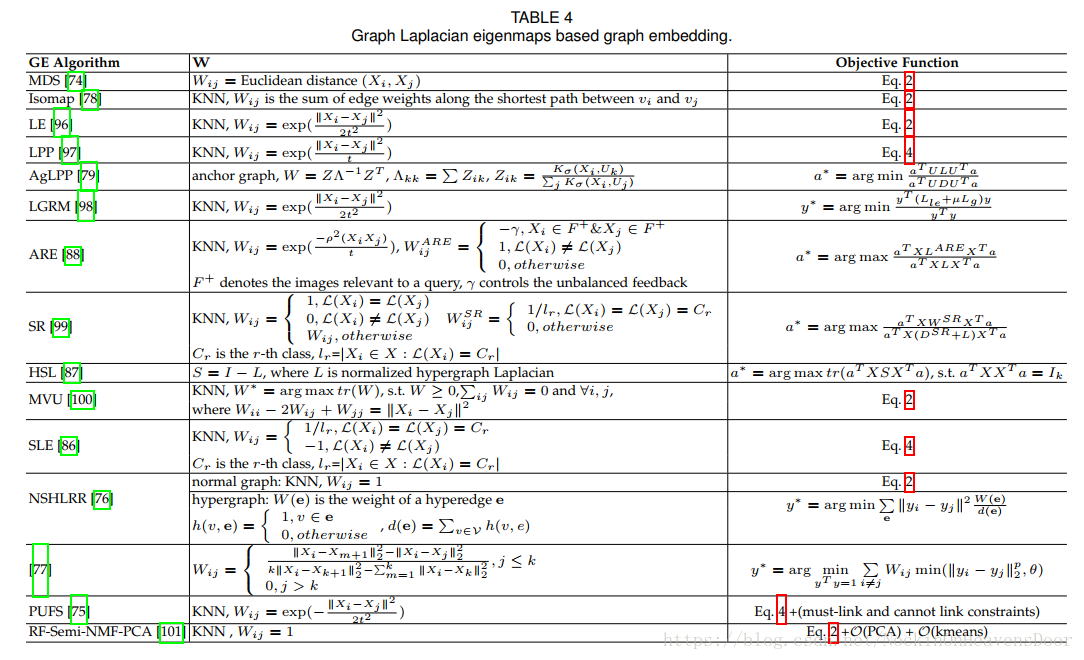
node proximity matrix factorization
**Insight:**直接用矩阵分解近似得到节点相似性,目标就是减少近似所产生的loss。
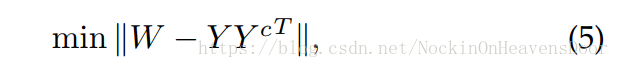
显然
W
W
W 是节点相似性矩阵,
Y
Y
Y 是节点的embedding,
Y
c
Y^c
Yc 是上下文节点(context nodes)的embedding。一种方法是对
W
W
W做SVD得到:
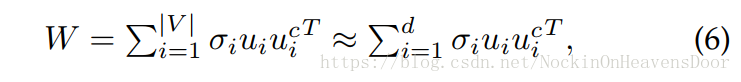
可以看出来,取出最大的
d
d
d 个特征分解近似
W
W
W,那么
Y
Y
Y 的embedding就是:
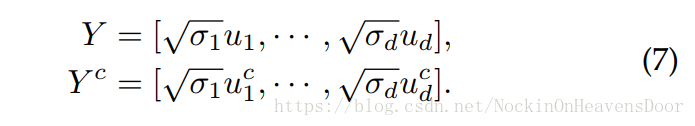
衍生:

深度学习
DL :有 随机游走
**Insight:**二阶邻近性的保留:最大化给定节点的embedding,出现该节点邻居(上下文节点)
的概率。
这里的图被表示为一系列随机游走路径的采样。用SkipGram模型(最大化词与词之间的共现概率,所以有相同neiborhoods的节点共享相似的embedding,其中用的截断随机游走(truncated SW),即均匀的在最后游走的节点上采样连接点,直到大小等于窗口大小
W
W
W):
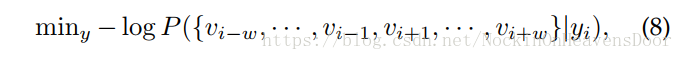
skipgram取消采样顺序的限制:
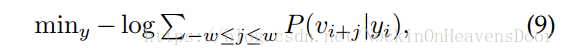
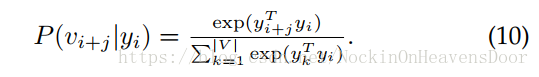
公式(10)的计算技巧有两种:
-
分层softmax(Hierarchical softmax):
-
负采样(Negtive sampling):
衍生:
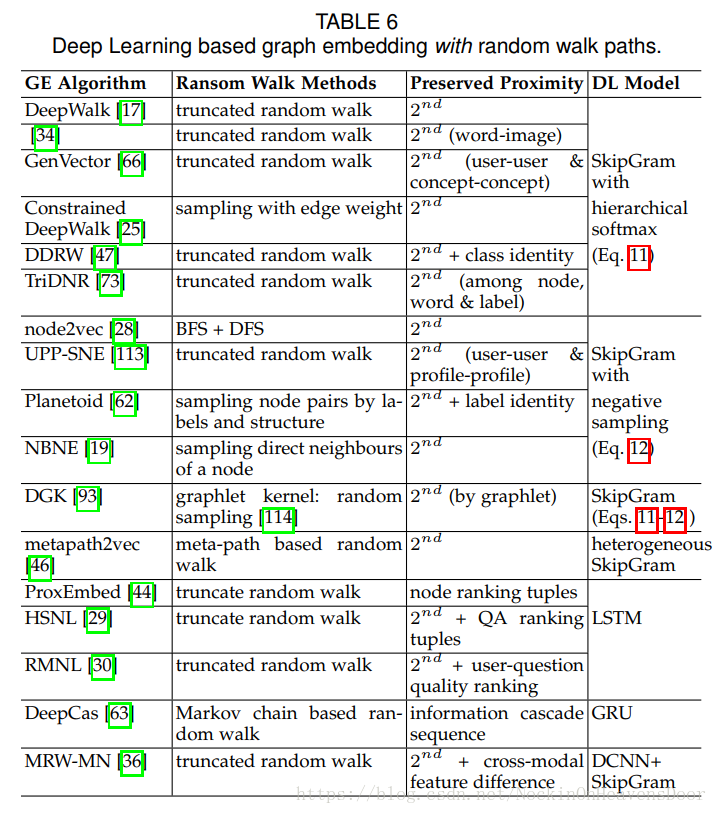
DL :无 随机游走
**Insight:**逐层的学习结构可以编码图到一个低维空间。(编码器)
- 自编码器:最小化重构损失,类似于节点相似性矩阵分解,因为输入的是邻接矩阵,自然coding层的embedding应该被解码为共享邻居节点的节点有相似的embedding。
- 深度神经网络:用CNNs来对图做卷积的方法。(未展开)
- 其他:用在异构网络、知识图谱等的各种神经网络的合成。
衍生:

重构图上的边(edge reconstruction)
**Overall Insight:**基于节点的embedding判断边是否和输入时有差不多的相似性,也就是直接对目标函数做优化。
总览:
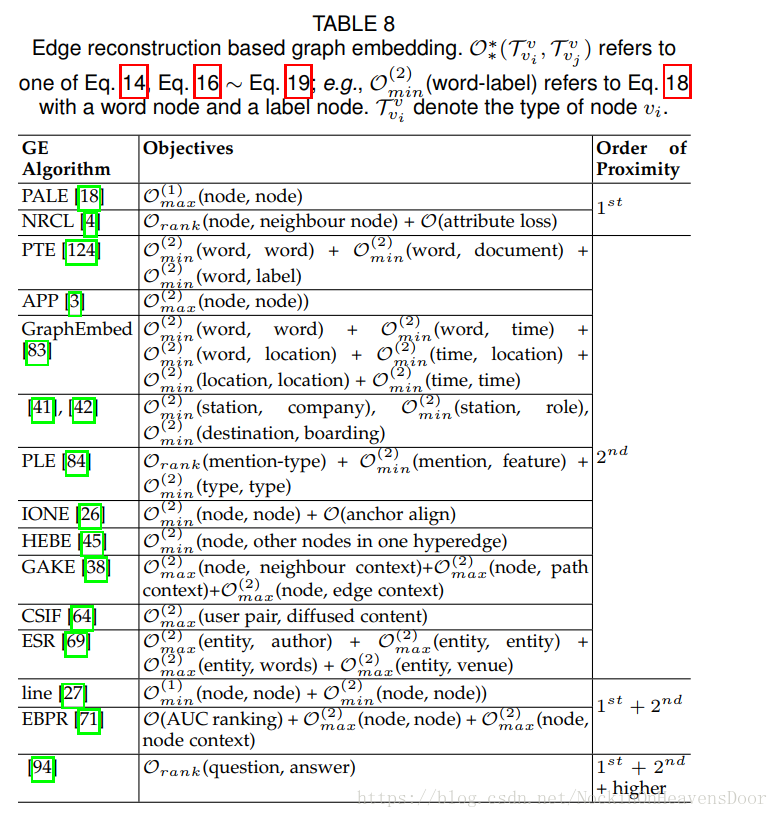
最大化边重构概率
Insight:怎样的节点embedding算是好的?可以最大化事件A发生的概率算好的。事件A:目标函数计算出现的边是图中已观测到的存在的边。
成对节点之间有边是一阶邻近性,其概率定义为:
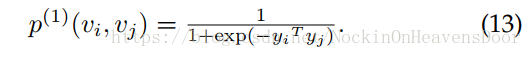
优化其log函数: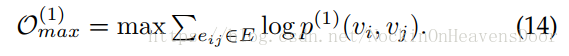
同样的,两点间二阶邻近性的概率:
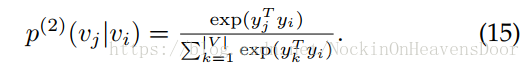
等价于从节点
v
i
v_i
vi 到
v
j
v_j
vj 的随机游走,优化的目标函数是:
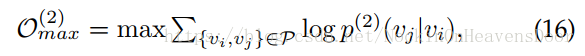
其中
P
\mathcal P
P 是随机游走的{起点,终点}路径集合。
基于距离的最小化损失
Insight:节点的embedding计算得到节点之间的邻近性,也可以从观测到的边来计算得到节点之间的邻近性,令这两种度量相等,减少彼此之间的误差。
用embedding计算一阶邻近可以用(13)计算得到;用观测到的边来计算
p
^
(
1
)
=
A
i
j
/
∑
e
i
j
∈
E
A
i
j
\hat p^{(1)}=A_{ij}/ \sum_{e_{ij}\in E} A_{ij}
p^(1)=Aij/∑eij∈EAij,其中
A
i
j
A_{ij}
Aij 是边
e
i
j
e_{ij}
eij 的权重,然后用KL散度度量
p
(
1
)
p^{(1)}
p(1) 和
p
^
(
1
)
\hat p^{(1)}
p^(1) 的距离,忽略一些常数得目标函数:
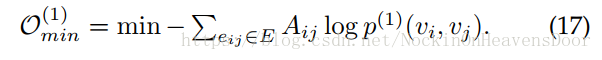
同样,二阶邻近用(15)计算得到;$\hat p^{(2)}(v_j \vert v_i)=A_{ij} / d_i $ ,其中
d
i
=
∑
e
i
k
∈
E
A
i
k
d_i =\sum_{e_{ik}\in E}A_{ik}
di=∑eik∈EAik 代表节点
v
i
v_i
vi的出度或者度。
用KL散度度量 $ p^{(2)}(v_j \vert v_i)$ 和
p
^
(
2
)
(
v
j
∣
v
i
)
\hat p^{(2)}(v_j \vert v_i)
p^(2)(vj∣vi)得到目标函数:
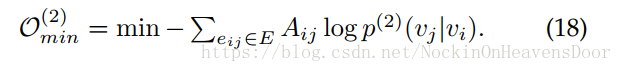
基于边缘距离的排名(Margin-based Ranking)最小化损失
Insight:例子:问答网站中,给定的一个问题有很多回答,则这些回答和该问题就是相关的。则该问题的embedding应该与这些相关回答的embedding接近,而与不相关的回答隔得远。
记
s
(
v
i
,
v
j
)
s(v_i,v_j)
s(vi,vj) 是节点
v
i
v_i
vi 和
v
j
v_j
vj 的相似度得分,
V
i
+
V_i^+
Vi+ 是与节点
v
i
v_i
vi 的相关节点集合,同样
V
i
−
V_i^-
Vi− 是不相关节点集合。则损失函数定义是:
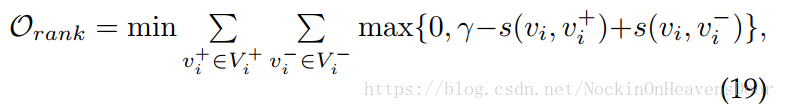
其中
γ
\gamma
γ 是一个边缘(margin)大小,最小化这个函数的效果就是让
s
(
v
i
,
v
i
+
)
s(v_i,v_i^+)
s(vi,vi+) 和 $ s(v_i,v_i^-)$ 之间产生一个大的margin。
注:知识图谱的embedding:大多属于此类型。一个KG记为
G
\mathcal G
G,有很多三元组
<
h
,
r
,
t
>
<h,r,t>
<h,r,t>组成,对
G
\mathcal G
G 做embedding,即尽可能保留正样本
<
h
,
r
,
t
>
< h ,r, t >
<h,r,t>的排名而不是假样本
<
h
′
,
r
,
t
′
>
< h^{'} ,r, t^{'} >
<h′,r,t′>的排名。定义一个**
f
r
(
h
,
t
)
f_r(h, t)
fr(h,t) :即
h
h
h 和
t
t
t 的embedding在关系
r
r
r 下的距离得分函数**;比如transE的距离得分函数定义为:
∣
∣
h
+
r
−
t
∣
∣
l
1
|| h + r - t ||_{l1}
∣∣h+r−t∣∣l1 。
(19)在KG下是:
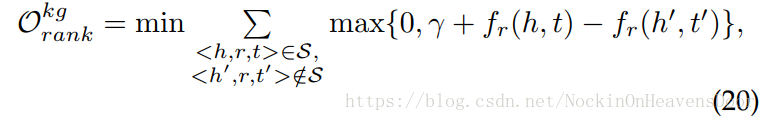
衍生:

图核(graph kernel)
- 目的是得到全图的全局信息,通常是处理异构图和带额外信息的图。
- 对结构
结论:全图生成一个embedding,所以用图的全局性质做embedding。输入常是同质图和带额外信息的图。
##生成模型
Embed Graph Into The Latent Semantic Space
**Insight:**图的节点都看做隐随机变量,边由节点分布生成,从而得到整个图,如LDA。假设的embedding space是latent space。
Incorporate Latent Semantics for Graph Embedding
Insight:接近的节点和有相似语义的节点应该embedding相似。而节点的语义可以通过生成模型处理节点的描述来获取。如KB的多关系类型的语义结合:结合三元组和实体、关系的语义描述生成embedding,常常涉及两个空间,语义空间和三元组的隐空间。利用隐空间整合节点或者边的额外信息在另一个空间生成新的(enhanced)embedding。
结论:生成模型考虑了节点语义,所以输入常常是异构图或者带额外信息的图。
##综合模型、其他
多种不同模型生成的混合模型。
总结

矩阵分解时间空间上消耗大,但在特定任务上由于DL;DL的优势在于捕捉复杂的图结构信息,DL加随机游走的缺点是注重节点的局部邻居而忽视了全局意义上的信息,找不到最优的采样策略,因为embedding和路径采样不在一个框架上进行优化;DL 无随机游走的计算代价高;边重构比上面两种更加高效,但是都是注意局部信息缺少对全局意义上的关注;图核的缺地是子结构之间不是独立的,子结构之间存在冗余(redundant information),embedding的维度随着子结构的增加而指数增长;生成模型在同一框架下对不同信息源的信息做embedding,假设的分布难以验证,需要的数据量大,不适合训练小图和少量的几个图。
应用
节点应用
节点分类
- 用带标签的节点embedding训练分类器(SVM,Logistic regression,k-nearest neighbour等),然后判断无标签的节点embedding属于什么类别。
- 同时进行节点embedding和节点分类的训练,生成分类明确的节点embedding。
节点聚类
- k-means用在节点embedding上。
- 同时聚类和学习节点embedding,生成聚类明确的节点embedding。
节点推荐\检索\排序
- KG中的实体排名,即给出三元组中的关系和一个实体,预测另一个缺失的实体等。
边应用
连接预测
- 真实图的信息往往不完整,比如用户之间相识却没有边存在,则预测边的存在即是连接预测。
三元组分类
- 判断 < h , r , t > <h,r,t> <h,r,t> 是否正确,比如 h h h 和$ t$ 之间的 r r r 是否存在。
图应用
图分类
- 整个图带一个标签,比如化学复合物、组织分子、蛋白质结构等。
可视化
其他应用
KG相关:
在文本中抽取实例,文本信息与KB的实体做连接等。
多媒体网络:
降维做脸部识别,图像、文本的embedding。
信息传递:
社交网络对齐、图像相关的embedding
未来的方向
##计算性方面
DL用GPU加速,但是图不具有格结构(grid structure)所以需要新的方法提高效率。
问题方面
动态图做embedding:图结构随着时间在改变、节点\边被时间因素影响。
技术方面
边重构需要具有结构意识(structure awareness),但是目前的边重构方法主要对1-hop的边做重构,这提供了边的局部信息,但是忽略了边的全局信息(如路径,树,子图模式等),所以有些工作如探索KB的paths信息。但是都是用的DL的方法(缺点:效率),怎么设计非DL的方法是个问题。所以图的子结构embedding,结合子结构采样是目前需要的。
应用
不同源的数据在同一空间做embedding,使之可比较。
#总结
如上的工作创新。





 本文全面概述了图嵌入的概念、问题形式化及其在不同场景下的应用。详细介绍了图嵌入的技术方法,包括矩阵分解、深度学习、边重构等,并探讨了未来的发展趋势。
本文全面概述了图嵌入的概念、问题形式化及其在不同场景下的应用。详细介绍了图嵌入的技术方法,包括矩阵分解、深度学习、边重构等,并探讨了未来的发展趋势。
















 7723
7723

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








