今天无意中看见了该算法十字交叉法计算矩阵,瞬间一脸懵逼,这和我学的竟是一个东西?!所以又去翻了翻书看概念然后理解该方法……啊,其实是一样的啊!废话不多说,谈谈新的理解吧
关于十字交叉算法戳戳这位博主 链接: link.
一、概念:
该算法针对解决图中任意两结点间的最短路径问题,考虑的是一条最短路径的中间结点,本质思想是动态规划,可以存在负权重的边,但不能出现负权重的环(由于是写理解,仅列出本人认为该算法需要注意到的点,关于具体概念自己动手翻书啦)
二、实现:
根据我们以往经验,如果要让任意两点之间路程可能变短,只能引入第三个点k,有时候甚至需要引入多个点才能实现这一目标,下面我们将这个问题一般化:
当任意两点间不允许有其他点存在时的最短路径就为初始路径,如下图:

现在我们为了缩短距离,允许任意两点间最多再经过 1 号顶点 ,此时对任意两点 i , j 间的最短距离distance(n+1) [i][j] 有 : distance(n+1)[i][j] = min{ distance(n) [i][j] , distance[i][1] + distance[1 ][ j ] } .
路程全部更新一次后结果如下:

我们可以看到白色标记部分的路径长度通过中间结点 1 已经得到了缩短,如果此时条件变为任意两点间允许最多引入 1 ,2 两点,即在现有基础上 对中间结点 2 重复一遍上述操作,那么distance矩阵数据将会在现有基础上再次更新,
结果如下:

同理,此时条件在原来的基础上再依次加入结点3,结点4……一直到结点 n
(引入结点的先后顺序不影响最终结果,只是为了代码方便实现,n 为结点总个数)
说了大致思路,是时候给出核心代码啦!
(核心代码居然只有五行……)
for(k = 1;k <= n;k++)
for(i = 1;i <= n;i++)
for(j = 1;j <= n;j++)
if(distance[i][j] > distance[i][k] + distance[k][j] )
distance[i][j] = distance[i][k] + distance[k][j]
三、算法正确性分析:
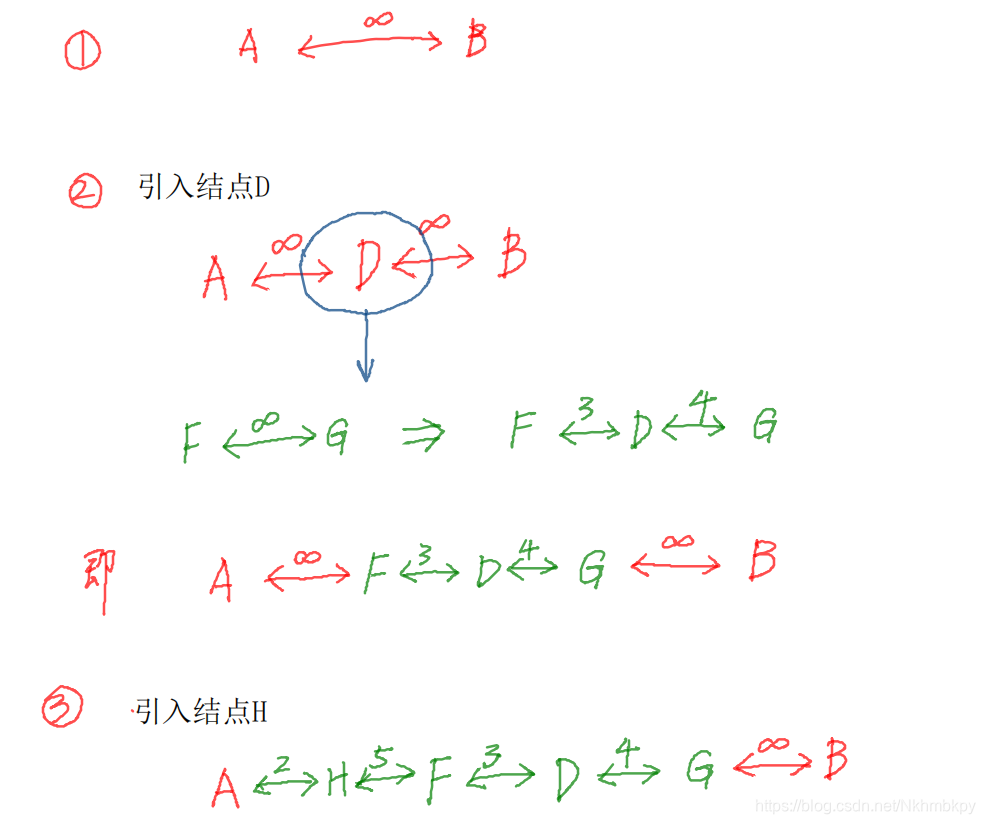
如上图所示,以AB两点间距离的松弛为例,还未进行松弛时,AB间距离无穷,
然后我们第一次松弛,引入结点D,但松弛不成功,D的引入并不能缩短AB间的距离……
但是!
我们把D周围放大来看:FG结点间的直接距离是无穷,但当D引入后,F间的距离缩短为7,
即
虽然我们试图缩短AB的距离不成功,但我们实现了把可能通向AB的路径上的某一段的距离缩短了!
返回去看代码,最外层把从0到n在任意两个结点间尝试插入,即便本次操作失败(如向AB中插入D)但对除操作失败的两点(除AB外的点,如FG两点)外其他的点的松弛成功可能为实现当前AB两点的松弛做铺垫!!!!而且松弛的先后顺序对最后的松弛结果没有影响,理由如下图:
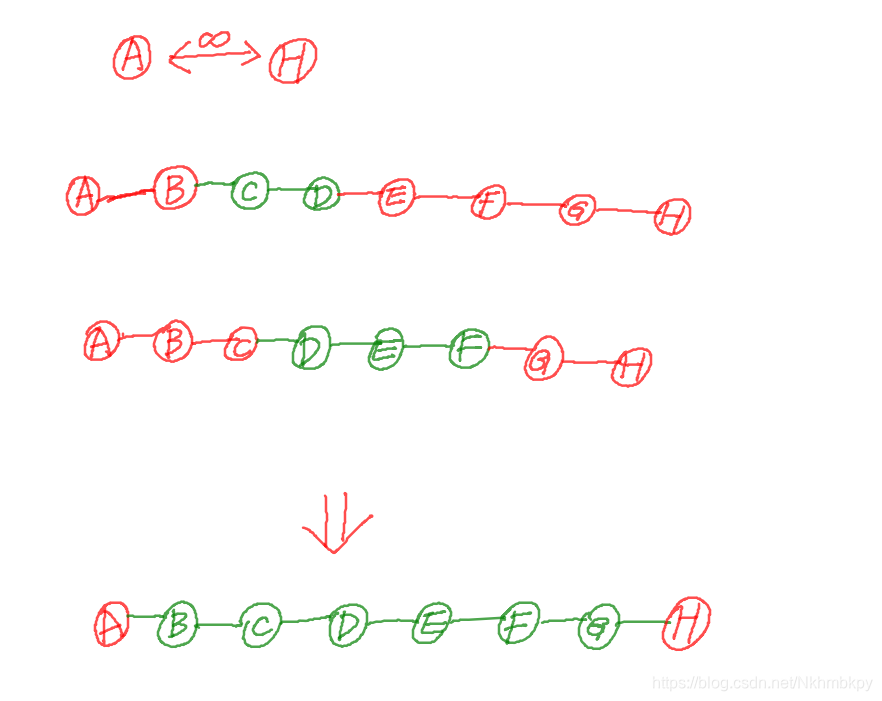
注:(绿色部分是已经通过松弛发现的可行路径,红色部分是还未进行恰当松弛操作的点)
遍历完1 ~ n 后,我们最终实现的结果是AH间的距离通过中间那些绿色的点得到了缩短,而不论是先实现中间结点BE通过CD两点的松弛得到缩短,还是中间结点CG通过DE得到缩短,只要将所有结点都遍历进行松弛操作,最后就一定能实现相同的松弛结果啦
四、十字交叉法的理解(针对文章开始那篇文啦,写的挺好)
FW算法的思想还是挺好懂的,毕竟就五行代码,但需要把每一次的松弛结果都写出来还是很烦人的(比如该死的数据结构作业……)一不小心就看走眼,并且松弛过程中有些计算是完全可以省略的,
比如 a[ 0 ] [ 0 ] = a[0][ i ] + a[ i ] [0 ] ,这个计算大可不必操作,但在实际计算中煞费苦心地避免他们还不如一股脑儿得算来得快与准,所以我选择了它……
拿那位博主的图说事吧
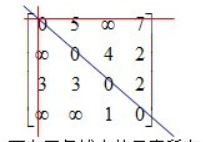
三条线交叉的元素就是本次用于松弛操作的元素,而划去的那些元素是本次整体松弛不需要考虑的元素,而用于松弛的两条边就是被松弛元素对应的两个行与列上的被划线元素,具体操作如下:
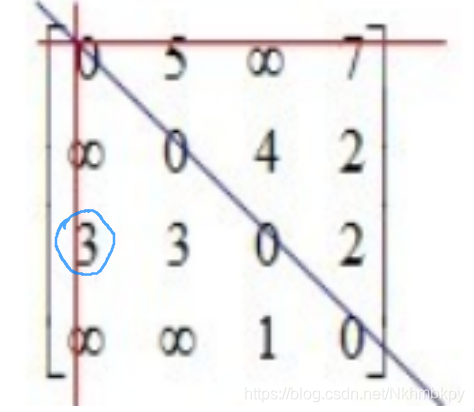
如圈出的3为例,此时用于松弛的是1号元素,松弛过程为 a[3][1] = a[ 3 ][1] + a[1 ][1] (多此一举……)
而没有被划去的元素则是需要计算松弛结果的,如下图:
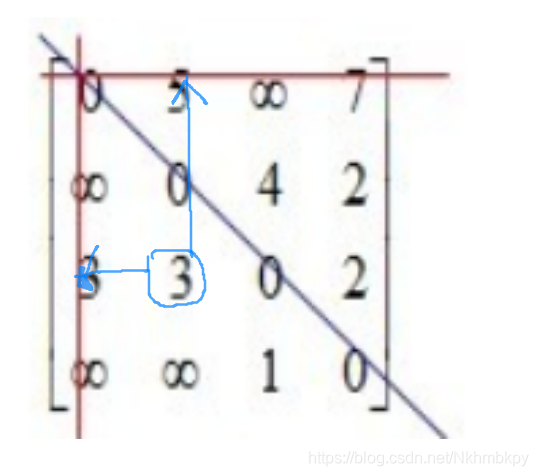
圈出的是需要松弛的元素,箭头所指即用于松弛的元素 ,?(a[3][2] = a[3][1] + a[1][3]) 由图可知
3 < 3+ 5 所以松弛不成功,对其他未被划线元素执行相同操作
当所有未被划线的元素都计算后,将十字沿着对角线下移:
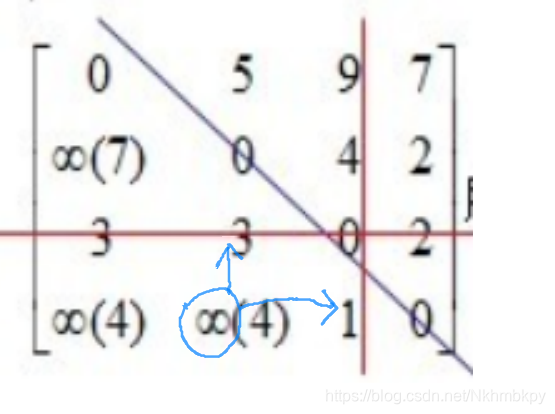
嗯,这张图更具有代表性就跳过一步啦……
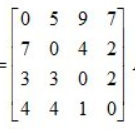
还是针对圈出来的未被划线的元素与之对应的划线行列上的两个元素是3,1,而3+1 显然能实现松弛,所以结果由无穷更新为4 ,本次用3号元素全部松弛后结果如下:





















 1299
1299

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








