二次递归c++内存的工作原理：为什么前序遍历、中序遍历、后续遍历函数大体是一样的却可以获得不同的结果（递归实现和栈实现）

原创已于 2022-06-19 11:01:20 修改 · 741 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#leetcode #数据结构 #深度优先遍历 #c语言 #逻辑回归

于 2022-05-16 20:17:10 首次发布

在数据结构中，排序、插入、遍历应用到了二次递归，二次递归一直是一个难点，大部分教材也一直解释不清，同时也是很多学校里的老师很少会花时间讲解的一个内容。

这里以前序遍历、中序遍历、后续遍历来表述二次递归中c++编译器中的工作原理。

先贴上前序遍历，中序遍历，后续遍历的代码

前序遍历（preorder)

void preorder_traversal(Treenode * root){
if(root ==NULL){
return;}
cout << "遍历发正在这里"<<root ->data<<endl;
preorder(root ->left);
preorder(root ->right);}

中序遍历（inorder）

void inorder_travsal(teende * root){
if(root = NULL){
return}
inorder_travsal(root ->left);
cout << "遍历发生在这里"<<root ->data<<endl;
inorder_travsal(root ->right);
}

后续遍历（postorder)

void postorder_traversal(treenode * root){
if(root == NULL){
return;}
postorder(root->left);
postorder(root ->right);
cout<<"遍历发生在这里"<<root ->data<<endl;}

仔细观察会发现这些函数的大体遍历十分相似。

而只有cout << 位置不同导致了输出结果的不同

但为什么会导致遍历的过程不同？

这与c++的内存机制有关，在c++中函数的递归其实是入栈和出栈的过程。（因为c++采用的是栈内存）

那么什么是栈（stack）呢？其实可以想象成一个弹夹，我们最后压入的子弹最先打出，栈遵循后进先出原则。

那么编译器是怎么想的呢？

我们举一个简单的例子：

void fun(int a){
if（ a<0){
return;}
fun(a-1)
cout << a<<endl;}

比如这行代码，当我们输入5时，输出会变成 0,1,2,3,4,5

为什么会这样呢？

因为之前提到过，c++递归本质上只是一个入栈和出栈的过程

我们输入5，5首先会被压入栈中，接着依次是4->3->2->1->0以此压入栈中，当变为-1时，递归函数触碰到了终止条件，return。接着栈里的元素一个接一个被弹出。

简化理解：每一次递归函数后，进入暂停状态，直到遇到return，继续向下执行

4(pause)->3(pause)->2(pause)->1(pause)->0（pause）-> -1(触碰到返回条件if(a<0)，不会继续进行递归）

0(continue)=>输出0

1（continue）=>输出1

.........

继续直到第一个暂停的状态被调用

这也是编译器中所发生的过程

接下来是DFS（前序，后续，中序遍历）

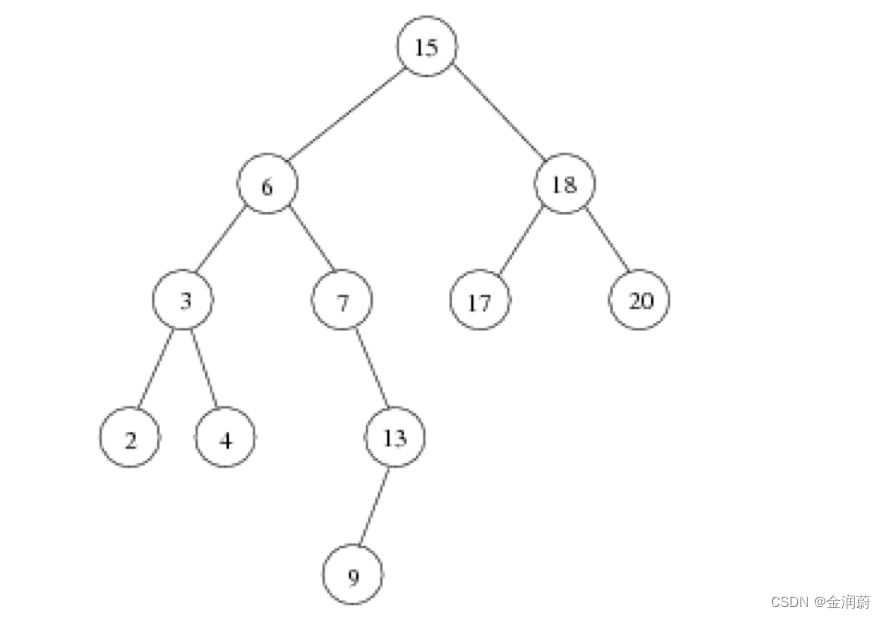
回到一开头的这张图

前序遍历(stack中）,先进行第一层的遍历

void preorder_traversal(Treenode * root){
if(root ==NULL){
return;}
cout << "遍历发正在这里"<<root ->data<<endl;
preorder(root ->left);

（打印15）15（pause)->（打印6）6(pause)->（打印3）3(pause)->（打印2）2(pause)->NULL(触碰返回条件：if(root ==NULL){return;}，不会再执行）

这些pause发生在preorder(root ->left)里

2(continue),给下一层递归函数，preorder(root ->right)

2的右边有null,又触碰到了返回条件，不会再执行

3(continue)->4(pause)(打印4)-> 然后观察这个函数：

发现第一层preorder(root ->left)，这个函数会被继续调用:4的左边NULL，触碰返回条件，不再执行。

前面的 4(continue)在preorder(root ->right)里继续调用，4的右边：NULL，触碰返回条件，不再执行。

6(continue):给下一层递归函数，preorder(root ->right)，6的右边：7(打印7）（pause在(r->right里）

7给到preorder(root ->left)里，继续递归，7的左边：NULL，不再执行。

回到（pause在(r->right），继续调用：打印13（pause)

13给到preorder(root ->left)里，13左边为9，打印（pause)，再次调用preorder(root ->left），9的左边为空，不再继续。

回到13:调用13preorder(root ->right)，为空，不再继续。

15（continue）：……

最后得到遍历的结果：preorder:15,6,3,2,4,7,13,9,18,17,20

获取遍历结果我们只需要观察cout在哪里即可

我们了解这个就会发现为什么在一些教材中会出现一个口诀：节点，左，右

其中一个规律：root节点永远出现在最左边

中序遍历：相同操作，也是出栈入栈过程

inorder：2,3,4,6,7,9,13,15,17,18,20

后续遍历：postorder ：2，4，3，9，13，7，6，17，20，18

强烈建议用纸和笔来多次练习一下！！！

我们观察前序遍历和中序遍历中，似乎可以不使用这种递归就可以得到相同的结果，因为正如前文中所说，一个"stack"栈的存在似乎也可以得到一样的结果！！！！

那么如何用栈来实现呢？

回顾整个遍历的过程我们会发现：我们只需要顺着根节点开始：把左边从第一个遇到的第一个节点依此压入栈里，全部压入栈里后，在把栈顶元素弹出向右边遍历一次再向左边持续遍历，这也是大体上来讲编译器中发生的过程。

前序遍历：

void iterative_inorder(Treenode * r){
if(root == NULL){
return;}
stack<Treenode *> treestack;
Treenode curr= r;
Treenode * temp  = NULL;
do(
   if(curr != NULL){
   treestack.push(curr);
    cout <<"遍历发生在这里"<< curr->data<<endl;
    curr = curr->left;
    else{
    temp = treestack.top();
    treestack.pop();
    curr = temp ->right;}while(!treestack.empty()||currnode != NULL)//有可能tree stack为空，但curr里仍然存贮这一个值
}

中序遍历：

void iterative_inorder(TreeNode *r){
    if(r== NULL){
        return;
    }
    else{
        TreeNode * currnode = r;
        TreeNode * prevnode = NULL;
        stack<TreeNode*>treestack;
        do{
            if(currnode!= NULL){
                treestack.push(currnode);
                currnode = currnode ->left;
            }
            else{
                prevnode=treestack.top();
                treestack.pop();
                cout <<"遍历发生在这里"<<prevnode ->data<<endl;
                prevnode = prevnode ->right;
                currnode = prevnode;
            }
    
        }while(currnode!=NULL||!treestack.empty());
    }
}

和前面一样的道理。

而后续遍历我们发现是沿着一个节点，先遍历左边，左边结束了在遍历右边，右边结束了才会遍历到这个节点，这里应该使用两个栈来实现，一个主栈，用来实现进入和遍历，另外一个栈用来判断当前节点的右边是否遍历到了（因为和前面一样，先向左持续遍历下去），遍历到了才会遍历这个节点，再加上和递归方程一样的判断，（左边指针为空则从栈中弹出。向右边遍历一次，再持续向左边继续遍历）

void iterativePostorder(TreeNode* root){
    if(root == NULL){return;}
    else{
        TreeNode * cur = root;
        stack<TreeNode *>mainstack;
        stack<TreeNode *>rightstack;
        while(cur!= NULL || !mainstack.empty()){
            if(cur!=NULL){
            mainstack.push(cur);
            if(cur ->right !=NULL){
                rightstack.push(cur->right);
            }
            cur = cur ->left;
            }
            else{
                    cur = mainstack.top();
                    if(!rightstack.empty() && cur->right == rightstack.top()){
                        //意味着，我们还没有遍历植于右子节点的子树(右边没有遍历到，左边已经完全了）
                        //避免null = null
                        cur = rightstack.top();//cur继续遍历，遍历只发生在mainstack中
                        rightstack.pop();
                    }//ChildStack弹出顶部节点，并使用currNode分配它。
                    else{
                        mainstack.pop();
                        cout << cur ->data<<endl;
                        cur =NULL;
                    }
            
        }
    }
}
}

以上这些就是二次递归之--------深度优先遍历。

和数据结构有关的课程会慢慢更新，希望可以对学习有帮助。

Feel free to ask!!!