python版二分搜索算法

先用图展示一下二分搜索算法的原理

---

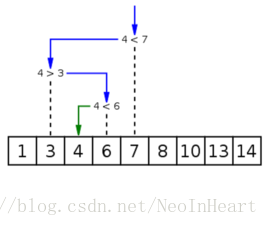
二分搜索算法又称为折半搜索，下面代码实现的是输出要搜索数据在数组中的位置和查找的次数：

算法的步骤：
给一个带有n个值的数组，数组A是从小到大的排列{A0,A1,…An-1}
需要查找T值在数组的中的位置
1、先令L为0，R为n-1
2、如果存在L>R,则不需进行搜索
3、令m（中间元素）为[（L+R）/2]
4、如果Am<T，令L=m+1返回第二步
5、如果Am>T，令R=m-1返回第二步
6、当Am=T时回传值m

#迭代版本

n=0
def dichotomy(arr,start,end,key):
    global n #如果要在函数中给全局变量赋值，需要用global关键字声明
    n+=1
    if end<start:
        return -1
    mid=start+int((end-start)/2)
    if arr[mid]<key:
        return dichotomy(arr,mid+1,end,key)
    elif arr[mid]>key:
        return dichotomy(arr,start,mid-1,key)
    else:
        return mid,n

#while的方法进行查找

def dichotomy_search(arr,start,end,key):
    n=0
    while start<=end:
        n+=1
        mid=start+int((end-start)/2)
        if arr[mid]<key:
            start=mid+1
        elif arr[mid]>key:
            end=mid-1
        else:
            return mid ,n

arr=[1,2,3,4,5,6,7,9,11,12,15,17,20,21,23]
a,b=dichotomy(arr,0,14,3)
print("方法一：\n查找的位置：%d\n查找的次数：%d\n"%(a,b))
c,d=dichotomy_search(arr,0,14,17)
print("方法二：\n查找的位置：%d\n查找的次数：%d\n"%(c,d))

输出的结果：

方法一：
查找的位置：2
查找的次数：4

方法二：
查找的位置：11
查找的次数：2