《利用Python进行数据分析》笔记（1）——第四章：Numpy模块

1. 创建ndarry

ndarry就是n维数组

1.1 用np.array(列表、元组等)函数

用np.array()创建数组

import numpy as np #导入Numpy模块

#将一个元组转换成一维数组
data1 = (2, 4, 6.7) 
array1 = np.array(data1) 
array1
Out[8]: array([ 2. ,  4. ,  6.7])

#将一个等长的嵌套元组转换成二维数组
data2 = ((7, 90,8), (1, 4.5, 0))
array2 = np.array(data2) 
arrary2
Out[11]: 
array([[  7. ,  90. ,   8. ],
       [  1. ,   4.5,   0. ]])

用数组名.ndim 数组名.shape查看数组属性

#查看array2的维度和几行几列
array2.ndim
Out[13]: 2

array2.shape
Out[14]: (2, 3)

1.2用np.zeros/ones/empty/arange/eye创建特殊数组

用np.zeros()创建全是0的数组 np.ones()同理

np.zeros(4)
Out[15]: array([ 0.,  0.,  0.,  0.])

np.zeros((4,5))
Out[16]: 
array([[ 0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.]])

用np.empty()创建垃圾值数组（即任意值，注意不是创建出全是0的数组）

np.empty((2,4))
Out[17]: 
array([[  0.00000000e+000,  -1.49166824e-154,   2.12688503e-314,
          2.34664926e-314],
       [  0.00000000e+000,   0.00000000e+000,  -1.72723382e-077,
          5.56268610e-309]])

用np.arrange()创建有序数组（range的数组版本，从0开始，只能有一个参数）

np.arange(9)
Out[18]: array([0, 1, 2, 3, 4, 5, 6, 7, 8])

用np.eye()创建对角矩阵（只用传一个参数）

np.eye(5)
Out[22]: 
array([[ 1.,  0.,  0.,  0.,  0.],
       [ 0.,  1.,  0.,  0.,  0.],
       [ 0.,  0.,  1.,  0.,  0.],
       [ 0.,  0.,  0.,  1.,  0.],
       [ 0.,  0.,  0.,  0.,  1.]])

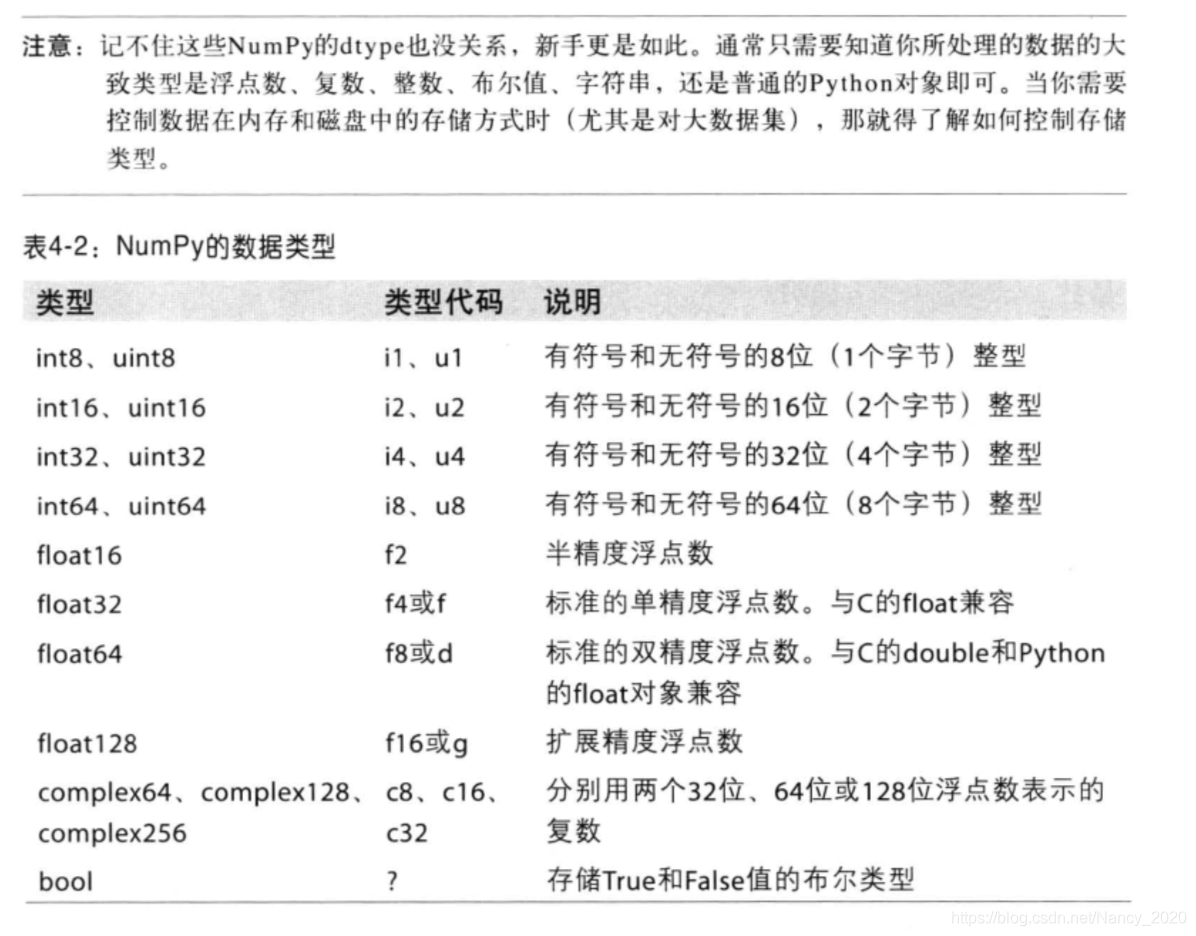
2. ndarry的数据类型

可以用dtype控制ndarry的存储类型

arr1 = np.array([1, 2, 3], dtype=np.float64)
arr2 = np.array([1, 2, 3], dtype=np.int32)

arr1.dtype
Out[31]: dtype('float64')

arr2.dtype
Out[32]: dtype('int32')

用数组名.astype(数据类型)转换dtype
用astype无论如何都会创建出一个新的数组（即使是类型相同，也相当于一份拷贝）

#整型int和浮点型float的dtype转换
arr = np.array([1, 2, 3], dtype=np.int32)
float_arr = arr.astype(np.float64)

float_arr.dtype
Out[35]: dtype('float64')

#字符串str和浮点型float的dtype转换
numeric_strings = np.array(["1.2", "3.4"], dtype=np.string_)#这里有一个小_
numeric_strings.dtype
Out[41]: dtype('S3')

numeric_strings.astype(float)
Out[42]: array([ 1.2,  3.4])

数据类型可以直接表示为另一个数组名.dtype使两个数组的数据类型相同

arr1 = np.arange(10)
arr2 = np.array([1, 3], dtype=np.float64)

arr1.astype(arr2.dtype)
Out[46]: array([ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9.])

3. 数组和标量之间的运算

• 数组与数组之间的运算

大小相等的数组之间的任何运算都会应用到元素级（对应位置元素相加减）；大小不同的数组之间的运算（叫broadcasting广播，第12章介绍）

arr = np.array([[1, 2, 3],[1, 2, 3]])

arr-arr
Out[49]: 
array([[0, 0, 0],
       [0, 0, 0]])

arr*arr
Out[50]: 
array([[1, 4, 9],
       [1, 4, 9]])

arr+arr
Out[51]: 
array([[2, 4, 6],
       [2, 4, 6]])

• 数组与标量之间的运算

标量作用于每一个元素

arr*3
Out[52]: 
array([[3, 6, 9],
       [3, 6, 9]])

4. 基本的索引和切片

基本的索引和切片的方法和list相同（从0开始）

arr = np.arange(10)

arr
Out[66]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

arr[5]
Out[67]: 5

#标量赋值给切片，“广播”到整个选区
arr[5:8] = 12
arr
Out[69]: array([ 0,  1,  2,  3,  4, 12, 12, 12,  8,  9])

和列表最大的区别：数组切片是原始数组的视图，视图上的任何修改都会反映到源数组上（没有数据的复制）
用数组名.copy(空)来复制数组

arr_slice = arr[5:8]
arr_slice[0] = 12345

arr_slice
Out[72]: array([12345,    12,    12])

#!!源数据也会被修改！！，NumPy设计的目的是 处理大数组，如果要将数据复制来复制去会产生内存和性能的问题
arr
Out[73]: array([    0,     1,     2,     3,     4, 12345,    12,    12,     8,     9])

不同维度的数组

#一维数组
arr1d = np.array([1,2,3])
arr1d
Out[56]: array([1, 2, 3])

#二维数组
arr2d = np.array([[1,2,3],[4,5,6]])
arr2d
Out[78]: 
array([[1, 2, 3],
       [4, 5, 6]])

#三维数组 一个2*2*3的数组
arr3d = np.array([[[1, 2, 3],[4, 5, 6]],[[7, 8, 9],[10, 11, 12]]])
arr3d
Out[60]: 
array([[[ 1,  2,  3],
        [ 4,  5,  6]],

       [[ 7,  8,  9],
        [10, 11, 12]]])

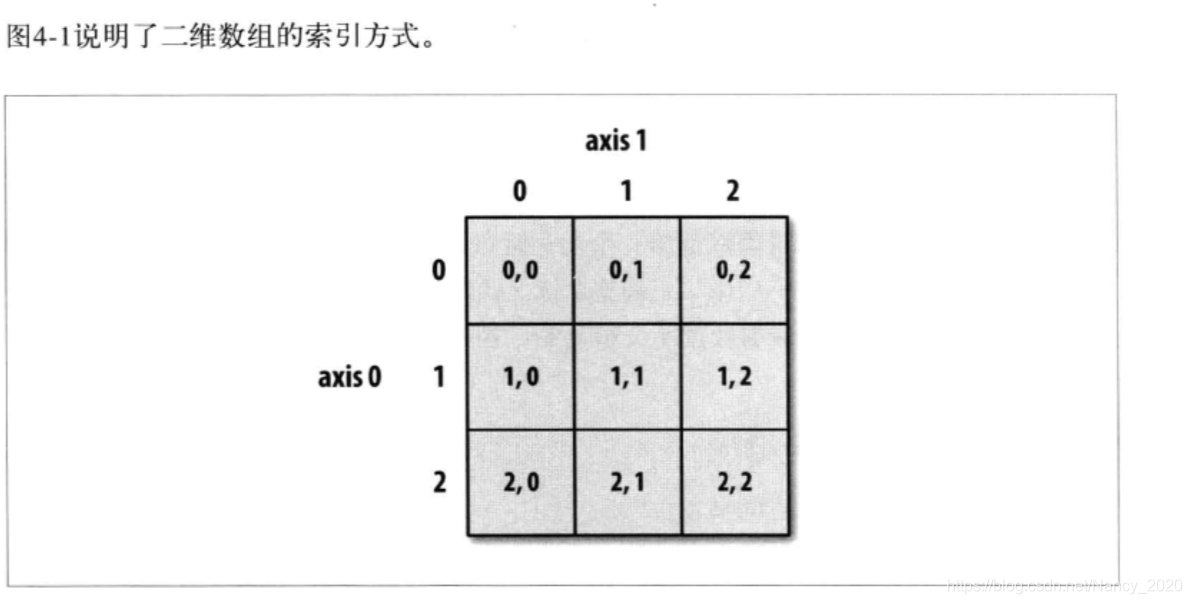
进一步看高维度数组的索引

1. 整数索引[0]
2. 切片索引[1:]

（！注意返回的数组都是视图）

#整数索引
#两种方法等价
arr2d[0,1]
Out[74]: 2

arr2d[0][1]
Out[75]: 2

arr2d[1]
Out[80]: array([4, 5, 6])

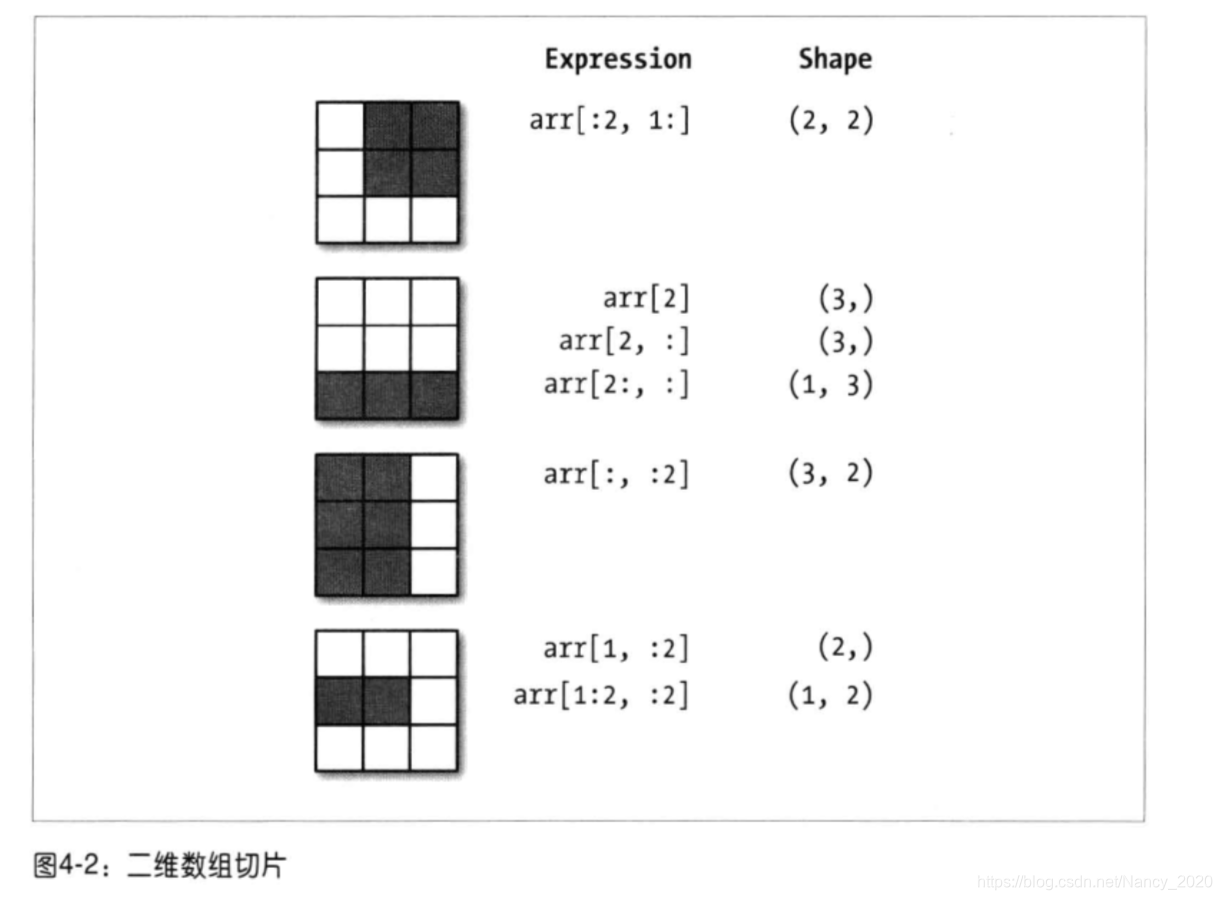
#切片索引（得到的和原来的数组维度相同）
arr2d
Out[91]: 
array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

arr2d[1:]
Out[92]: 
array([[4, 5, 6],
       [7, 8, 9]])

arr2d[:,:2]#对于第一个参数表示选取整个轴，必须只传入冒号：
Out[93]: 
array([[1, 2],
       [4, 5],
       [7, 8]])

#切片和整数混合索引（可得到和原来维度不同的视图）
arr2d[1,:2]
Out[96]: array([4, 5])


#一个2*2*3的三维数组
arr3d[0]#返回的是一个2*3的二维数组
Out[81]: 
array([[1, 2, 3],
       [4, 5, 6]])
  
arr3d[1, 0]#自己思考一下返回的应该是什么
Out[83]: array([7, 8, 9])

标量值和数组都可以赋值给arr3d[0]
用数组名.copy(空)来复制数组

#用`数组名.copy(空)`来保留原来的数据
old_values = arr3d[0].copy()

#标量赋值，全部变为这个值
arr3d[0] = 42
arr3d
Out[87]: 
array([[[42, 42, 42],
        [42, 42, 42]],

       [[ 7,  8,  9],
        [10, 11, 12]]])
#数组赋值
arr3d[0] = old_values
arr3d
Out[89]: 
array([[[ 1,  2,  3],
        [ 4,  5,  6]],

       [[ 7,  8,  9],
        [10, 11, 12]]])

3. 布尔型索引
4. 花式索引
   （！注意和1、2方法不同，返回的是一个新的数组）

布尔型索引

names = np.array(["Bob", "Joe", "Sue", "Joe"])

data =np.random.randn(4,3)#生成一个4*3的二维数组，元素是标准正态分布,假设每个名字对应一行

data
Out[103]: 
array([[ 0.72330428,  0.78923483, -0.63181156],
       [-1.25841267, -0.50450255,  0.29339865],
       [ 0.76848001, -1.52510875,  0.72306561],
       [-1.44503825, -0.37939587, -0.24318109]])

#选出Joe对应的行
names == "Joe"
Out[104]: array([False,  True, False,  True], dtype=bool)
data[names == "Joe"]
Out[105]: 
array([[-1.25841267, -0.50450255,  0.29339865],
       [-1.44503825, -0.37939587, -0.24318109]])

#布尔索引和1、2方法混合使用
data[names == "Joe",1:]
Out[107]: 
array([[-0.50450255,  0.29339865],
       [-0.37939587, -0.24318109]])


data[names != "Joe"]#data[-(names == "Joe")]效果一样
Out[108]: 
array([[ 0.72330428,  0.78923483, -0.63181156],
       [ 0.76848001, -1.52510875,  0.72306561]])

#用 |（或）、&（与）  and和or在布尔型数组中无效
mask = (names == "Joe") | (names == "Sue")
names[mask]
Out[113]: 
array(['Joe', 'Sue', 'Joe'], 
      dtype='<U3')
data[mask]
Out[114]: 
array([[-1.25841267, -0.50450255,  0.29339865],
       [ 0.76848001, -1.52510875,  0.72306561],
       [-1.44503825, -0.37939587, -0.24318109]])

#将data中所有负数改为0也很简单

data[data<0] = 0

data
Out[117]: 
array([[ 0.72330428,  0.78923483,  0.        ],
       [ 0.        ,  0.        ,  0.29339865],
       [ 0.76848001,  0.        ,  0.72306561],
       [ 0.        ,  0.        ,  0.        ]])

花式索引（Fancy indexing）是NumPy术语，指的是利用整数数组进行索引(和切片索引的区别：切片——按顺序，花式——跳着来,或者改变顺序)

#学习一下这种生成每一行元素为该行行序的数组
arr = np.empty((8,4))
for i in range(8):
    arr[i] = i
    
arr
Out[126]: 
array([[ 0.,  0.,  0.,  0.],
       [ 1.,  1.,  1.,  1.],
       [ 2.,  2.,  2.,  2.],
       [ 3.,  3.,  3.,  3.],
       [ 4.,  4.,  4.,  4.],
       [ 5.,  5.,  5.,  5.],
       [ 6.,  6.,  6.,  6.],
       [ 7.,  7.,  7.,  7.]])

#用list或者ndarry都可以
arr[[4, 3, 0, 6]]
Out[127]: 
array([[ 4.,  4.,  4.,  4.],
       [ 3.,  3.,  3.,  3.],
       [ 0.,  0.,  0.,  0.],
       [ 6.,  6.,  6.,  6.]])
#负数也可
arr[[-4, -5, -8, -2]]
Out[128]: 
array([[ 4.,  4.,  4.,  4.],
       [ 3.,  3.,  3.,  3.],
       [ 0.,  0.,  0.,  0.],
       [ 6.,  6.,  6.,  6.]])

一次传入多个索引的list有点特别
同时也学习一下这种range数组的生成方法
用数组名.reshape((n*m))来生成想要形状的数组

arr = np.arange(32).reshape(8, 4)

arr
Out[132]: 
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12, 13, 14, 15],
       [16, 17, 18, 19],
       [20, 21, 22, 23],
       [24, 25, 26, 27],
       [28, 29, 30, 31]])


arr[[1, 2],[2, 1]]
Out[135]: array([6, 9])#返回的结果是(1,2) (2,1)两个元素形成的一维数组


#要得到想象中的二维数组可以有两种方法
arr[[1, 2]][:,[2, 1]]
Out[137]: 
array([[ 6,  5],
       [10,  9]])
#或者用np.ix_函数
arr[np.ix_([1, 2],[2, 1])]
Out[140]: 
array([[ 6,  5],
       [10,  9]])

5.数组转置和轴对换

返回的是源数据的视图，不会进行复制

用np.dot()和数组名.T计算矩阵的内积$X^{T}X$

arr = np.random.randn(6,3)

arr
Out[143]: 
array([[ 0.09173806, -0.57002709, -1.17686837],
       [-0.55958403, -0.26004808, -0.00956899],
       [ 0.18164916, -0.91396507,  0.61415675],
       [-0.50981882, -1.18984593, -0.93930327],
       [-0.98936969,  0.3964252 ,  1.41860576],
       [ 0.18063364,  0.74315173,  0.20169237]])

np.dot(arr.T,arr)
Out[144]: 
array([[ 1.6259427 ,  0.27583756, -0.87926653],
       [ 0.27583756,  3.3530488 ,  1.94190271],
       [-0.87926653,  1.94190271,  4.697712  ]])

注：
高维数组的转置用transpose（）或者swapaxes（）接受一组轴编号

6.通用函数ufunc：对数组元素级进行运算

许多ufunc函数都是简单的元素级变体

• 一元ufunc函数

传入一个数组，如：np.sqrt（数组名）和np.exp（数组名）

arr = np.arange(10)

np.sqrt(arr)
Out[146]: 
array([ 0.        ,  1.        ,  1.41421356,  1.73205081,  2.        ,
        2.23606798,  2.44948974,  2.64575131,  2.82842712,  3.        ])

np.exp(arr)
Out[147]: 
array([  1.00000000e+00,   2.71828183e+00,   7.38905610e+00,
         2.00855369e+01,   5.45981500e+01,   1.48413159e+02,
         4.03428793e+02,   1.09663316e+03,   2.98095799e+03,
         8.10308393e+03])

• 二元ufunc函数
  传入两个数组如：np.maximum（数组1，数组2）

arr1 = np.array([1, 5, 2])

arr2 = np.array([2, 3, 0])

np.maximum(arr1, arr2)
Out[152]: array([2, 5, 2])

不常见：有些ufunc返回的是多个数组
如：np.modf（数组名）返回的是数组的小数和整数部分

np.modf(np.random.randn(8))
Out[154]: 
(array([ 0.91937754,  0.52040243,  0.30590146,  0.00800788,  0.58938351,
         0.09135368, -0.17263665, -0.5015982 ]),
 array([ 1.,  0.,  1.,  1.,  2.,  0., -1., -1.]))

7.利用数组进行数据处理

NumPy数组可以将许多种数据处理任务表述为简洁的数组表达式（否则需要用到循环）
失量化：用数组表达式代替循环

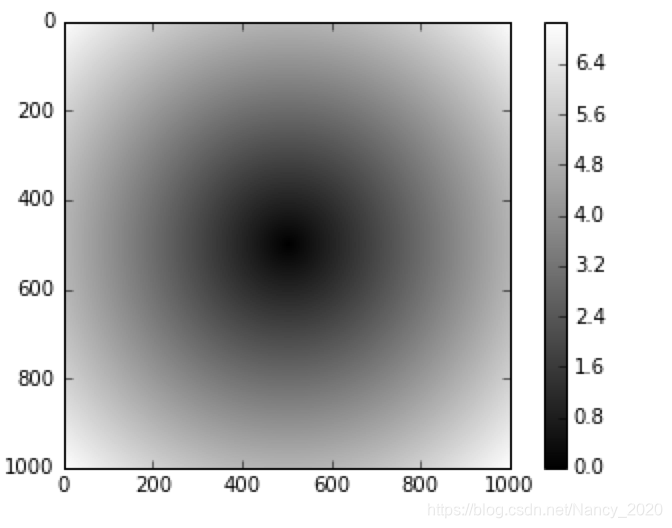
7.1 一个例子：画出在二维数轴（-5，5）矩形区域内的1000的散点组成的图

points = np.arange(-5, 5, 0.01)#1000个间隔相等的点

xs, ys = np.meshgrid(points, points)#meshgrid的适用于生成网格型数据,还不是很懂

ys
Out[157]: 
array([[-5.  , -5.  , -5.  , ..., -5.  , -5.  , -5.  ],
       [-4.99, -4.99, -4.99, ..., -4.99, -4.99, -4.99],
       [-4.98, -4.98, -4.98, ..., -4.98, -4.98, -4.98],
       ..., 
       [ 4.97,  4.97,  4.97, ...,  4.97,  4.97,  4.97],
       [ 4.98,  4.98,  4.98, ...,  4.98,  4.98,  4.98],
       [ 4.99,  4.99,  4.99, ...,  4.99,  4.99,  4.99]])

import matplotlib.pyplot as plt

z = np.sqrt(xs**2 + ys **2)
z
Out[161]: 
array([[ 7.07106781,  7.06400028,  7.05693985, ...,  7.04988652,
         7.05693985,  7.06400028],
       [ 7.06400028,  7.05692568,  7.04985815, ...,  7.04279774,
         7.04985815,  7.05692568],
       [ 7.05693985,  7.04985815,  7.04278354, ...,  7.03571603,
         7.04278354,  7.04985815],
       ..., 
       [ 7.04988652,  7.04279774,  7.03571603, ...,  7.0286414 ,
         7.03571603,  7.04279774],
       [ 7.05693985,  7.04985815,  7.04278354, ...,  7.03571603,
         7.04278354,  7.04985815],
       [ 7.06400028,  7.05692568,  7.04985815, ...,  7.04279774,
         7.04985815,  7.05692568]])

plt.imshow(z, cmap = plt.cm.gray);plt.colorbar()
Out[162]: <matplotlib.colorbar.Colorbar at 0x11dac8c88>
#诶，怎么在上面那个图里加标题呢？
plt.title("Image plot of $\sqrt{x^2+y^2}$ for a grid of values")
Out[163]: <matplotlib.text.Text at 0x122036f28>


7.2 用np.where将条件逻辑表述为数组运算

xarr = np.array([1, 2, 3, 4])

yarr = np.array([5, 6, 7, 8])

cond = np.array([True, False, False, True])

Task:根据cond，如果是True返回xarry中的值，如果是False返回yarry中的值

cond = np.array([True, False, False, True])

np.where(cond, xarr, yarr)
Out[168]: array([1, 6, 7, 4]

arr = np.random.randn(4,4)

arr
Out[170]: 
array([[ 0.40947865, -0.8301057 ,  0.07401997, -0.11131255],
       [ 0.50430279,  0.38552736, -0.4430593 ,  0.57947363],
       [ 0.53893383, -0.70803052, -1.29943593,  2.04856019],
       [-0.19455571,  1.19293111, -0.15763062, -1.45520859]])

Task:将arr中小于0的数换成2，其余不变

np.where(arr<0, 2, arr)
Out[171]: 
array([[ 0.40947865,  2.        ,  0.07401997,  2.        ],
       [ 0.50430279,  0.38552736,  2.        ,  0.57947363],
       [ 0.53893383,  2.        ,  2.        ,  2.04856019],
       [ 2.        ,  1.19293111,  2.        ,  2.        ]])

7.3数学和统计方法

对整个数组或者某个轴向的数据进行统计计算sum、mean、std…

1. 当作数组的实例方法调用 数组名.mean/sum()
   -arr.sum(axis=0) 列
   -arr.sum(axis=1) 行
2. 当作顶级NumPy函数使用 np.sum(数组名)

arr = np.arange(9).reshape(3,3)#记住这个生成数组的方式哈！.reshape(3,3)

arr
Out[175]: 
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])

arr.sum()
Out[176]: 36

arr.sum(0)#按列和
Out[177]: array([ 9, 12, 15])

arr.cumsum()#累计和
Out[178]: array([ 0,  1,  3,  6, 10, 15, 21, 28, 36])

arr.cumsum(0)#按列累计和
Out[179]: 
array([[ 0,  1,  2],
       [ 3,  5,  7],
       [ 9, 12, 15]])

np.sum(arr)
Out[180]: 36

arr = np.random.randn(3,5)
arr
Out[185]: 
array([[ 0.73025901, -1.22225533,  0.01915748,  1.56837349,  1.04893057],
       [ 0.62395984,  0.32705197,  1.51673428,  0.11598897,  0.11551994],
       [ 1.7416128 ,  0.25995503, -0.02800417, -0.60717941, -0.85808779]])

arr.argmax()#返回的是最大值的索引（位置）
Out[186]: 10

7.4用于布尔型数组的方法

sum常被用来对True计数

arr = np.random.randn(10)

arr
Out[188]: 
array([-1.45759571,  0.07820359,  0.85982441, -0.52573305, -0.6044672 ,
        0.37968718, -0.5441947 ,  1.13490428, -3.17255457,  0.18203208])

(arr>0).sum()#非常灵活的代码
Out[189]: 5

• 数组名.all()：是不是都为True
• 数组名.any()：是不是存在True

bools = np.array([True, False, False, False])

bools.any()
Out[192]: True

bools.all()
Out[193]: False

7.5排序

1. 顶级方法np.sort(数组名)返回的是已经排序（从小到大）的副本
2. 就地排序数组名.sort()会修改数组本身

arr = np.random.randn(5,3)

arr
Out[195]: 
array([[-2.04465723, -1.89121294, -2.03661756],
       [ 0.95531002, -0.92955749,  1.46345173],
       [ 0.21311224, -0.0519942 , -0.25566805],
       [-0.20553132, -1.18281039,  1.09934148],
       [ 0.78885631, -0.13992471, -0.9743008 ]])

arr.sort()#默认参数为1，按行来

arr#就地排序，改变源数组的顺序
Out[199]: 
array([[-2.04465723, -2.03661756, -1.89121294],
       [-0.92955749,  0.95531002,  1.46345173],
       [-0.25566805, -0.0519942 ,  0.21311224],
       [-1.18281039, -0.20553132,  1.09934148],
       [-0.9743008 , -0.13992471,  0.78885631]])

Task：应用：找出5%分位数

large_arr = np.random.randn(1000)

large_arr.sort()#先排序

large_arr[int(0.05*len(large_arr))]#找出5%分位数
Out[208]: -1.5543440684657757

7.6唯一化以及其他的集合逻辑

• 用np.unique(数组名)找出数组中的唯一值
• 用np.in1d(x, y)测试数组x中的值在另一个数组y中的成员资格 (x是否在y中)

#找出数组中的唯一值
names = np.array(["Bob", "Joe", "Sam", "Joe", "Bob"])

np.unique(names)
Out[210]: 
array(['Bob', 'Joe', 'Sam'], 
      dtype='<U3')
      
#测试数组x中的值在另一个数组y中的成员资格 
values = np.array([1, 2, 3, 4, 8, 9, 0])

np.in1d(values, [2,3,6])
Out[212]: array([False,  True,  True, False, False, False, False], dtype=bool)    

8.用于数组的文件输入输出

8.1将数组以二进制格式保存到磁盘

用np.save(“数组名”, 数组)和np.load(“数组名”)来存、读
（np.savez(“名”, a = arr，b=arr )将多个数组保存在压缩文件中，arr是要保存的数组，以a、b关键字参数传入 ）
默认：数组以原始二进制格式保存在.npy文件中（.npy会被自动加上）

arr = np.arange(10)

arr
Out[214]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

np.save("some_arr", arr)#.npy会被自动加上

np.load("some_arr.npy")#读取文件的时候记得有.npy
Out[217]: array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

arr1 = np.arange(3)

arr2 = np.arange(5)

np.savez("package.npz", a = arr1, b = arr2)#压缩包是.npz

arch = np.load("package.npz")

arch["a"]
Out[222]: array([0, 1, 2])

8.2存取txt文件

用np.loadtxt(“.txt文件名”, delimiter = ",")读取txt文件
np.savetxt(）反操作

9.线性代数

矩阵乘法：x.dot(y)或者np.dot(x, y)

x = np.array([[1., 2.,3.],[4., 5.,6.]])

y = np.array([[6., 23.],[-1., 7.],[8., 9.]])

x,y
Out[227]: 
(array([[ 1.,  2.,  3.],
        [ 4.,  5.,  6.]]), array([[  6.,  23.],
        [ -1.,   7.],
        [  8.,   9.]]))

x.dot(y)#相当于np.dot(x, y)
Out[228]: 
array([[  28.,   64.],
       [  67.,  181.]])

np.dot(x, np.ones(3))#不太理解这个结果
Out[233]: array([  6.,  15.])

from numpy.linalg import inv, qr

arr = np.random.randn(5,5)

mat = arr.T.dot(arr)

mat.dot(inv(mat))#按理说应该出现的是5*5的E，可能是小数位数的问题
Out[258]: 
array([[  1.00000000e+00,   7.15611840e-14,  -4.67771998e-14,
          8.94356226e-14,   0.00000000e+00],
       [  3.60681390e-14,   1.00000000e+00,  -2.85287700e-13,
         -6.63461427e-13,  -1.13686838e-13],
       [  1.80184127e-14,   4.25329645e-13,   1.00000000e+00,
         -5.57892094e-13,   0.00000000e+00],
       [ -1.19598595e-13,  -6.29680483e-13,  -6.85462339e-13,
          1.00000000e+00,   1.70530257e-13],
       [ -5.68434189e-14,   0.00000000e+00,   0.00000000e+00,
          4.54747351e-13,   1.00000000e+00]])

10.随机数生成

• Python内置random模块只能一次生成一个样本值
• numpy.random可以生成大量的样本值

from random import normalvariate

N = 1000000

#用%timit查看运行的时间
%timeit samples = [normalvariate(0, 1) for _ in range(N)]#xrange 和range的区别
1 loops, best of 3: 752 ms per loop

%timeit np.random.normal(size = N)
10 loops, best of 3: 31 ms per loop

10.1范例：随机漫步

（1）通过内置的random模块以纯Python的方式实现1000步的随机漫步
（2）从0开始，步长1和-1的概率相等

import random

position = 0

walk = [position]

steps = 1000

for i in range(steps):
    step = 1 if random.randint(0, 1) else -1
    position += step
    walk.append(position)

其实就是随机漫步中各步的累积和，可以用一个数组运算来实现

nsteps = 1000
draws = np.random.randint(0, 2, size = nsteps)
steps = np.where(draws >0 , 1, -1)
walks = steps.cumsum()

#np.random.randint和random.randint上下限问题
np.random.randint(0,3,10)#不包含上限
Out[283]: array([0, 0, 0, 0, 1, 0, 1, 2, 2, 0])

random.randint(0,3)#包含上限
Out[285]: 3

random.randint(0,3)
Out[286]: 1

Task：首次穿越时间——想知道本次随机漫步要多久才能距离0点10步远（不管方向）

#argmax返回的是该布尔型数组第一个最大值的索引，然而效率不高：需要扫描所有的数组值
(np.abs(walk)>= 10).argmax()
Out[303]: 52

10.2一次模拟多个随机漫步

想模拟多个随机漫步过程（比如5000个）

nwalks = 5000

nsteps = 1000

draws = np.random.randint(0, 2, size = (nwalks, nsteps))

steps = np.where(draws >0, -1, 1)

walks = steps.cumsum()

walks = steps.cumsum(1)#记得是每一行累加

walks
Out[311]: 
array([[ -1,  -2,  -3, ..., -34, -35, -34],
       [  1,   0,  -1, ..., -40, -41, -42],
       [  1,   2,   3, ...,  32,  31,  32],
       ..., 
       [  1,   0,   1, ...,  12,  13,  14],
       [  1,   2,   3, ...,  -6,  -5,  -6],
       [ -1,   0,  -1, ...,   2,   3,   2]])

Task：首次穿越时间——计算30或-30最小穿越时间
（难点：不是5000次都穿越了30/-30）

hits30 = (np.abs(walks)>= 30).any(1)#用any筛选出穿越了30/-30的过程

hits30
Out[313]: array([ True,  True,  True, ..., False, False, False], dtype=bool)

hits30.sum()#可以算出有多少过程穿越了30/-30
Out[314]: 3376

crossing_time = (np.abs(walks[hits30])>=30).argmax(1)

crossing_time.mean()
Out[316]: 501.53021327014216

也可以用其他分部步方式得到随机漫步数据，如normal