数据结构之顺序表

最新推荐文章于 2024-03-27 01:21:32 发布

原创最新推荐文章于 2024-03-27 01:21:32 发布 · 691 阅读

1 ·

CC 4.0 BY-SA版权

数据结构专栏收录该内容

19 篇文章

订阅专栏

什么是线性表

线性表就是n个具有相同特性的数据元素的有限序列。它在逻辑上是线性结构，在物理结构上却不一定是连续的，线性表在物理上存储时，通常以数组和链式结构的形式存储。
常见的线性表有：顺序表、链表、栈、队列、字符串等。
首先我来介绍顺序表。

顺序表

概念：
所谓顺序表，就是用一段物理地址连续的存储单元依次存储数据元素的线性结构，一般情况下采用数组存储。
实现：
在实现顺序表之前，我们先定义一个接口IArrayList，来说明要实现的功能：

public interface IArrayList {
    /**
     * 把item插入到线性表的前面
     * @param item 要插入的数据
     */
    void pushFront(int item);

    /**
     * 把item插入到线性表的最后
     * @param item
     */
    void pushBack(int item);

    /**
     * 把item插入到index下标位置处，index后的数据后移
     * @param item
     * @param index
     */
    void add(int item,int index);

    /**
     * 删除前面的数据
     */
    void popFront();

    /**
     * 删除最后的数据
     */
    void popBack();

    /**
     * 删除index处的数据，index后的数据前移
     * @param index
     */
    void remove(int index);
}

再写一个类MyArrayList来实现之前写的那个接口，这一部分我会分开来介绍，首先我们需要定义一个array数组和一个整型常量size，array数组是用来保存数据的空间，size是保存有效数据的个数，接着我们要写一个构造方法来初始化函数，如下所示：

private int[] array;   
    private int size;      

    MyArrayList(int capacity){
        this.array = new int[capacity];
        this.size = 0;
    }

接下来就是具体实现了。
第一个功能是头插，头插就是将数组里的现有元素全部往后移一个，空出第一个位置，将我们要插入的数据放进去，需要注意的是，在往后移的过程中，必须从后往前移，否则会覆盖掉一些数据。用下面这个例子来说：
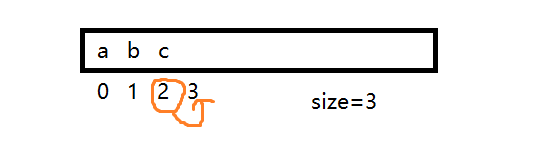
在这里插入图片描述
我们需要把a,b,c依次往后移一位，从后往前移的意思就是先移动c，最后移动a。在移动的过程中，有两种方法，根据数据的下标和根据空间下标来移动，这两种方法都需要考虑边界值。
数据下标：[size-1,0]
空间下标：[size,1]
采用for循环，将顺序表中已有的数据往后移一格，代码中我使用的是空间下标，所以移动的时候就是将array[i-1]的数据赋给array[i]，最后将要插入的数据放入array[0]，然后有效数据个数加1。

//时间复杂度O(n)
public void pushFront(int item) {
		//ensureCapacity();
        //将顺序表中已有的数据后移一格
        for (int i=this.size;i>=1;i--){
            this.array[i] = this.array[i-1];
        }
        this.array[0] = item;
        this.size++;
    }

第二个功能是尾插，顾名思义，就是在数组的最后边插入一个数据，这个相对来说比较简单，只需要将我们要插入的数据放到array[size]的位置即可，最后记得将有效数据个数加1.

//时间复杂度O(1)
    public void pushBack(int item) {
    	//ensureCapacity();
        this.array[this.size] = item;
        this.size++;
    }

第三个功能是在中间插入一个数据，这个其实跟头插比较相似，只是将最后一个挪动的位置稍加改变，比如说，如果按照空间下标移动，它的边界值为[size,index+1]，而如果按照数据下标来移动，它的边界值就是[size-1,index]。
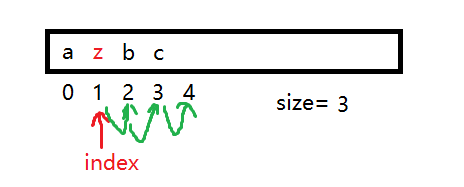
在这里插入图片描述

//时间复杂度O(n)
    public void add(int item, int index) {
        //ensureCapacity();
        if (index<0 || index>this.size){
            throw new Error();
        }
        for (int i=this.size;i>=index+1;i--){
            this.array[i] = this.array[i-1];
        }
        this.array[index] = item;
        this.size++;
    }

第四个功能是头删，从前往后覆盖就可以实现，空间下标的边界值：[0,size-2]，数据下标边界值：[1,size-1]，代码里采用的是数据下标，覆盖的时候将array[i]的数据赋给array[i-1]。

//时间复杂度O(n)
    public void popFront() {
        if (this.size == 0){
            throw new Error();
        }
        for (int i=1;i<=this.size-1;i++){
            this.array[i-1] = this.array[i];
        }
        this.size--;
    }

第五个功能是尾删，最简单的一个，直接将有效数据个数减1就行。

//时间复杂度O(1)
    public void popBack() {
        if (this.size==0){
            throw new Error();
        }
        this.size--;
    }

第六个功能是删除中间某个元素，类似于头删，更改第一个要挪动的位置即可，空间下标边界值：[index,size-2]，数据下标边界值：[index+1，size-1]。
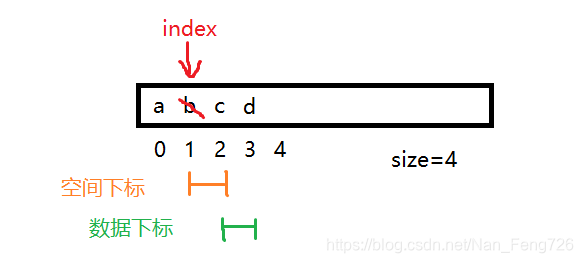
在这里插入图片描述

//时间复杂度O(n)
    public void remove(int index) {
        if (index<0 || index>=this.size){
            throw new Error();
        }
        if (this.size == 0){
            throw new Error();
        }
        for (int i=index+1;i<=this.size-1;i++){
            this.array[i-1] = this.array[i];
        }
        this.size--;
    }

上面实现的是一个静态的顺序表，只适用于知道需要存多少数据的场景。静态顺序表的定长数组导致N定大了，造成空间浪费，小了又不够用。所以实际中用的都是动态顺序表，根据需要动态分配空间的大小。
动态顺序表就是使用动态开辟的数组存储数据，假如数组放不下了，就需要扩容，就跟房子不够住需要换一个大房子是一样的道理。this.array是住的老房子，this.size是房子里住的人，我们应该先找一个新房子，然后搬家，再告诉this.array新房子的地址，最后退掉老房子。
需要注意的是，扩容后的数组大小一般为原来数组大小的2倍。

/**
     * 保证数组容量够用
     * 时间复杂度O(n)
     */
    private void ensureCapacity(){
        if (this.size<this.array.length){
            return;
        }
        //1、找新房子，找原来的2倍大小
        int capacity = this.array.length*2;
        int[] newArray = new int[capacity];
        //2、搬家
        for (int i=0;i<this.size;i++){
            newArray[i] = this.array[i];
        }
        //3、去学校登记新房子位置，退掉老房子
        this.array = newArray;
    }