C++：AVL树

最新推荐文章于 2024-09-08 17:49:57 发布
原创 最新推荐文章于 2024-09-08 17:49:57 发布 · 1k 阅读 · 8 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#数据结构 #c++ #开发语言 #visual studio

本文围绕AVL树展开，介绍了其概念、节点定义。重点讲解了AVL树的插入操作及插入后对平衡因子的影响，还详细阐述了四种旋转情况，包括右单旋、左单旋、先左旋再右旋、先右单旋再左单旋，最后提及AVL树性能，未详述删除操作。

1.1 AVL树的概念

二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查
找元素相当于在顺序表中搜索元素，效率低下。
但在AVL树中，任一节点对应的两棵子树的最大高度差为1，因此它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下时间复杂度都是 log_2(n);
AVL 树得名于它的发明者家G.M.Adelson-Velskii 和 E.M.Landis，他们在1962年的论文《An algorithm for the organization of information》中公开了这一数据结构。
对于一颗VAL树，它要么是一颗空树，要么就是一棵树具有以下性质的二叉树搜索树：
1.它的左右子树都是AVL树
2.左右子树高度之差(简称平衡因子)的绝对值不超过1(-1/0/1)

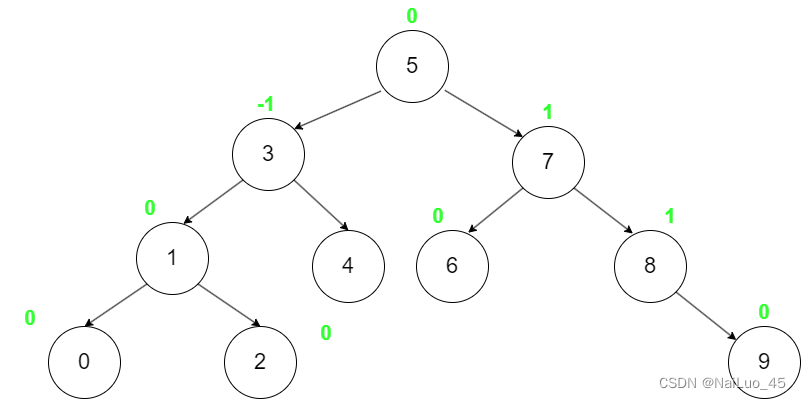
2.1AVL树节点的定义 

//AVL树节点的定义
template <class K, class V>
struct AVLTreeNode
{
	AVLTreeNode<K, V>* _left; //左子树
	AVLTreeNode<K, V>* _right; //右子树
	AVLTreeNode<K, V>* _parent; //父节点
	int _bf;   //平衡因子
	pair<K, V> _kv; 

	AVLTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_bf(0)
		,_kv(kv)
	{}
};

注：这里的平衡因子的值是用右子树高度减左子树高度，也可以反过来；另外，平衡因子只是辅助作用，AVL树可以不用平衡因子这个成员 

3.1AVL树的插入

AVL树就是在二叉搜索树的基础上引入了平衡因子，因此AVL树也可以看成是二叉搜索树。那么
AVL树的插入过程可以分为两步：
1. 按照二叉搜索树的方式插入新节点
2. 调整节点的平衡因子
bool Insert(const pair<K, V>& kv)   //插入
{
	if (_root == nullptr)
	{
		_root = new Node(kv);

		return true;
	}

	Node* cur = _root;
	Node* parent = nullptr;

    // 先按照二叉搜索树的规则将节点插入到AVL树中
	while (cur)
	{
		if (kv.first > cur->_kv.first)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (kv.first < cur->_kv.first)
		{
			parent = cur;
			cur = cur->_left;
		}
		else
			return false;
	}

	cur = new Node(kv);
	if (kv.first > parent->_kv.first)
	{
		parent->_right = cur;
	}
	else //(kv.first < parent->_kv.first)
	{
		parent->_left = cur;
	}

	cur->_parent = parent;  

// 新节点插入后，AVL树的平衡性可能会遭到破坏，此时就需要更新平衡因子，并检测是否
//破坏了AVL树的平衡性


	//更新bf信息
	while (parent)
	{
		//
	}

	return true;
}

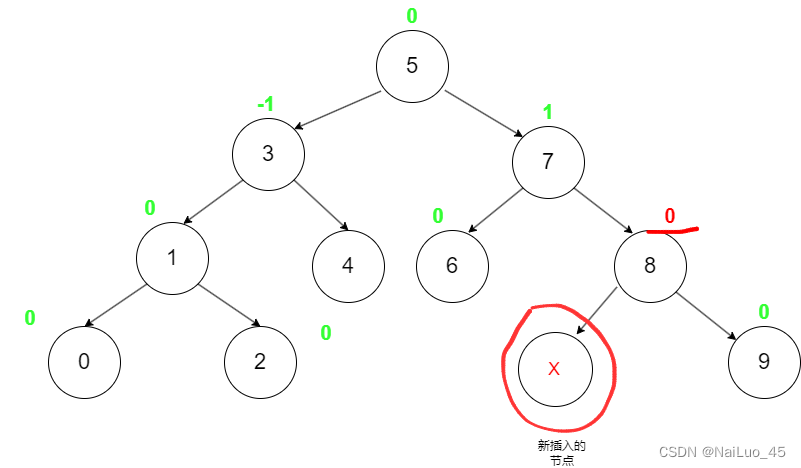
插入后，parent的平衡因子一定会被影响，插入前分为三种：1、0、-1

插入后的影响有以下这两种：

 1. 如果pCur插入到parent的左侧，只需给parent的平衡因子-1
 2. 如果pCur插入到parent的右侧，只需给parent的平衡因子+1
//更新bf信息
	while (parent)
	{
		//插入节点时，其父节点的平衡因子必定受到影响
        if (cur == parent->_left)
	        parent->_bf--;
        else
	        parent->_bf++;  

        //......
	}
此时：parent的平衡因子可能有三种情况：0，正负1， 正负2
1.如果parent的平衡因子为0，说明在插入之前parent的平衡因子为正负1，插入后刚好平衡;
        

2.如果parent的平衡因子为正负1，说明在插入之前parent的平衡因子为0，插入后更新为正负1，
此时以parent为根节点的树高度增加，应该继续向上更新（祖先节点平衡因子可能受到影响）；

3.如果parent的平衡因子为正负2，则parent的平衡因子违反平衡树的性质，需要对其进

行旋转处理；

	//更新bf信息
	while (parent)
	{
		//插入节点时，其父节点的平衡因子必定受到影响
		if (cur == parent->_left)
			parent->_bf--;
		else
			parent->_bf++;   

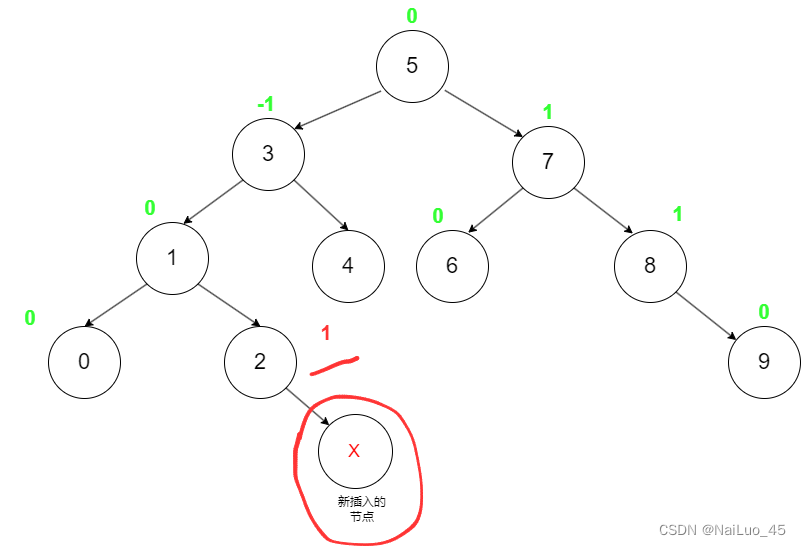
		//根据父节点的平衡因子，看祖先平衡是否被影响
		if (parent->_bf == 0)   
		{
			break;	    //bf 为0，插入并不会引起祖先平衡变化
		}
		else if (parent->_bf == 1 || parent->_bf == -1)  //对于祖先来说，它的子树高度变化                        
                                                         //了，会影响平衡
		{
			cur = cur->_parent;
			parent = parent->_parent;    //往上继续更新
		}
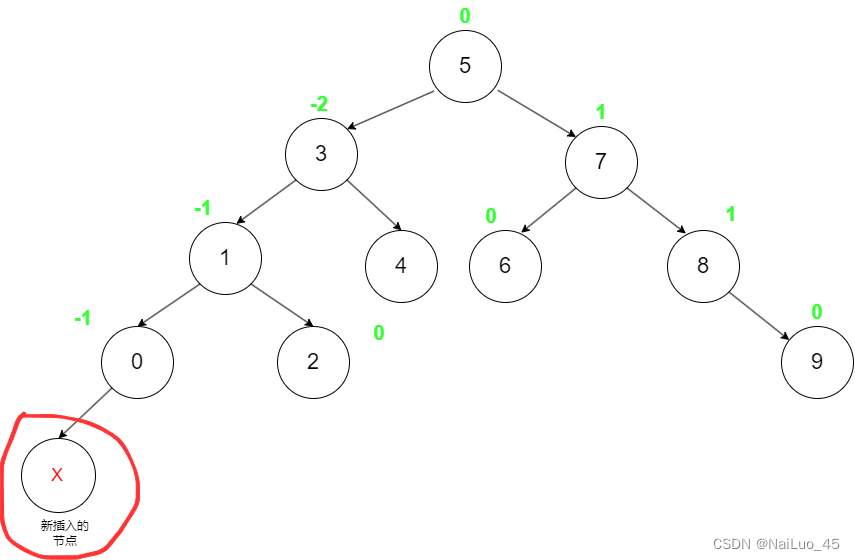
		else if (parent->_bf == 2 || parent->_bf == -2)
		{
			//旋转处理

			break;
		}
		else   //AVL树再插入之前有问题
		{
			assert(false);
		}

	}

	return true;
}

4.1 AVL树的旋转

 其实构成旋转条件的插入情况有很多种，可以根据子树高度，细分为多种插入情况，特别是子树高度很高时，情况非常多；因此，我们不应该过多关注节点插在一个什么样子的二叉树，应该关注高度变化。

4.1.1 新节点插入较高左子树的左侧——右单旋

例：

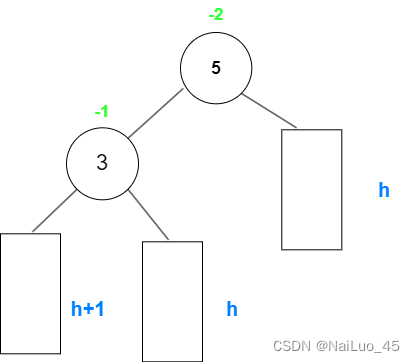
 忽略二叉树的结构，只考虑高度，可以把二叉树抽象为这个样子。

可以观察到：“5”的左子树高度导致不平衡，具体为“3”的左子树插入新节点引起高度变化；

想要平衡，“3”这棵树的高度需要降低，那么就让“3”去作为整棵树的根节点；

此时，“3”的左子树的高度为h+1，想要右子树平衡一下，应该让“5”与其右子树作为“3”的右子树，

这样就凑出h+1的高度，最后为了保持二叉树，“3”的右子树变为“5”的左子树。

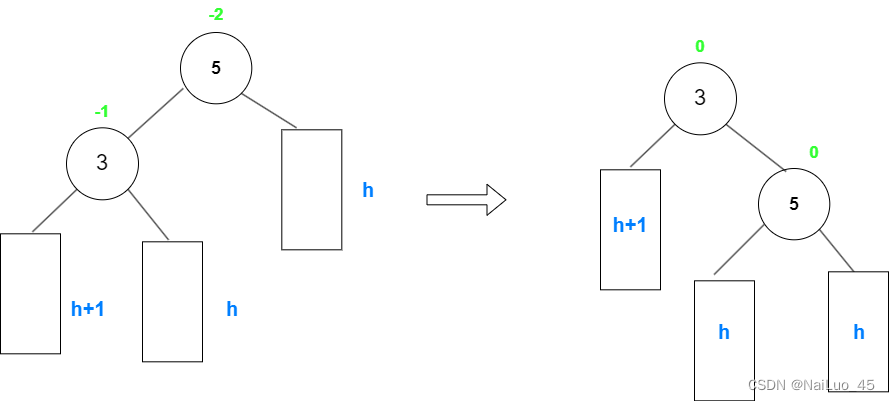
以上操作，条件是父节点平衡因子为-2，左子树为-1；

需要被操作的节点是“5”——parent指针；

“3”节点——用subL指针来操作，subL = parent->_left;

“3”节点的左子树——用subRL来操作，subLR = subL->_right; 由于左子树可能为空，所以这个指针也可能为空。

void RotateR(Node* parent)
{
	Node* subL = parent->_left;
	Node* subLR = subL->_right;

	parent->_left = subLR;
	if (subLR)
		subLR->_parent = parent;

	Node* ppnode = parent->_parent;//需要记录一下父节点的父节点,为了更新双亲
	subL->_right = parent;
	parent->_parent = subL;

	if (_root == parent) //父节点是整棵树的根节点
	{
		_root = subL;
		subL->_parent = nullptr;
	}
	else  //祖先节点与subL的连接
	{
		if (ppnode->_left == parent)
		{
			ppnode->_left = subL;
		}
		else
		{
			ppnode->_right = subL; 
		}

		subL->_parent = ppnode;
	}

    //更新平衡因子
	parent->_bf = 0;
	subL->_bf = 0;
}

4.1.2 新节点插入较高右子树的右侧——左单旋

例：

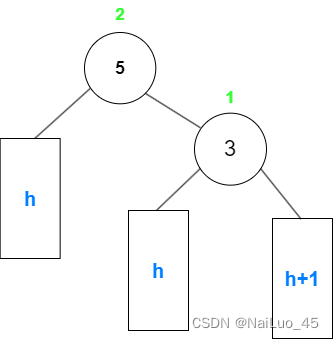
可以观察到：“5”的右子树高度导致不平衡，具体为“3”的右子树插入新节点引起高度变化；

想要平衡，“3”这棵树的高度需要降低，那么就让“3”去作为整棵树的根节点；

此时，“3”的右边子树的高度为h+1，想要右子树平衡一下，应该让“5”与其右边子树作为“3”的左子树，

这样就凑出h+1的高度，最后为了保持二叉树，“3”的左子树变为“5”的右子树。

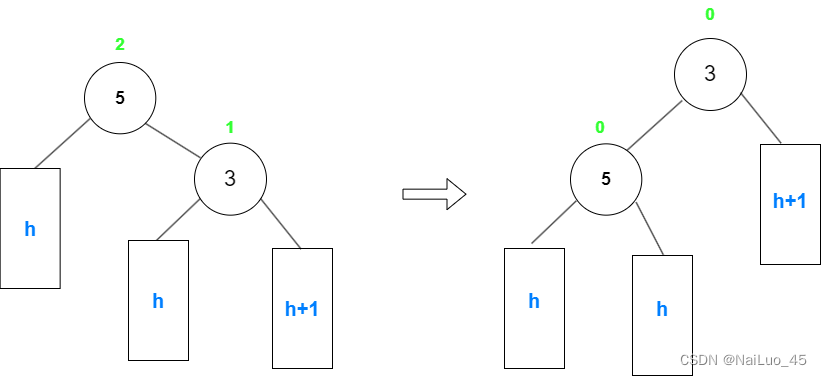
以上操作，条件是父节点平衡因子为-2，左子树为-1；

需要被操作的节点是“5”——parent指针；

“3”节点——用subR指针来操作，subR = parent->_right;

“3”节点的右子树——用subRL来操作，subRL = subL->_left; 由于左子树可能为空，所以这个指针也可能为空。

void RotateL(Node* parent)
{
	Node* subR = parent->_right;
	Node* subRL = subR->_left;

	parent->_right = subRL;
	if(subRL)
		subRL->_parent = parent;

	Node* ppnode = parent->_parent;
	subR->_left = parent;
	parent->_parent = subR;

	if (_root == parent)
	{
		_root = subR;
		subR->_parent = nullptr;
	}
	else
	{
		if (ppnode->_left == parent)
		{
			ppnode->_left = subR;
		}
		else
		{
			ppnode->_right = subR;
		}

		subR->_parent = ppnode;
	}

	subR->_bf = 0;
	parent->_bf = 0;
}

 4.1.3 新节点插入较高左子树的右侧——先左旋再右旋

例：

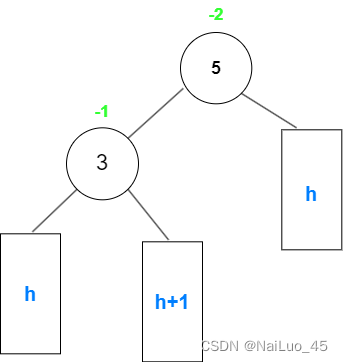
 这种情况，直接开转得不到什么结果，应该将“h+1”的树拆成左右子树将双旋变成单旋后再旋转：

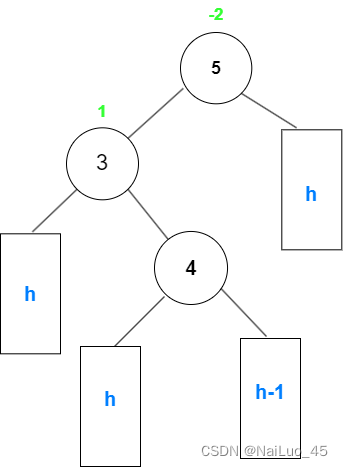
可以观察到：“4”节点左子树插入了一个节点导致整棵树不平衡，“4”这棵树相当于“3”的右子树是较高树的情况，所以对“3”进行左旋；

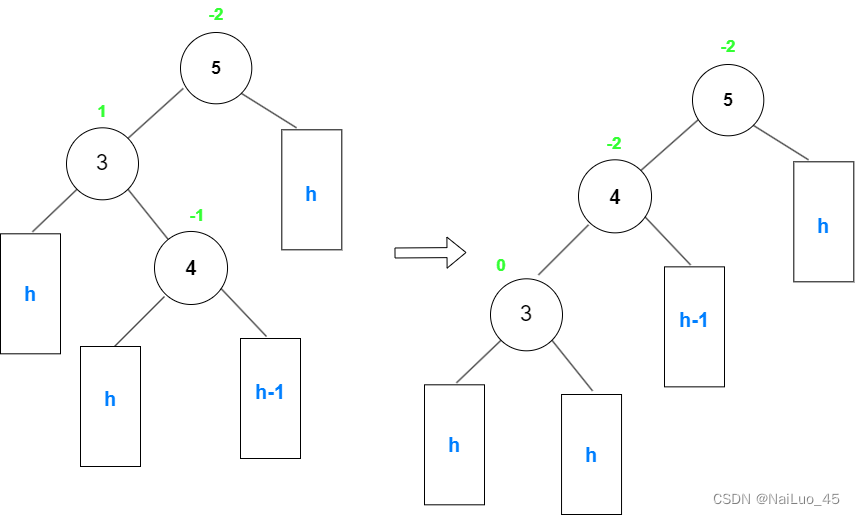
此时，“3”这棵树相当于 本来是“4”的左子树插入了新节点导致不平衡，应该对“4”进行右单旋。

 

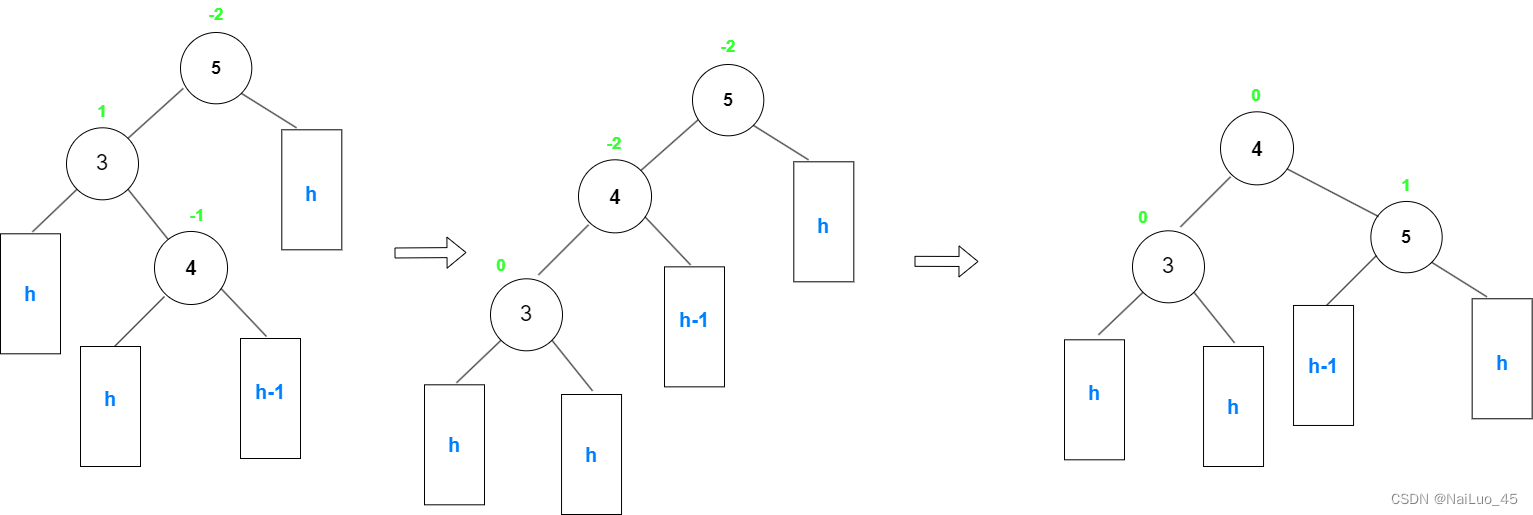
实现代码时，左右旋转只需要复用前面的代码就行，可是双旋完后的平衡因子调节比较麻烦；

上面例子是新节点插在“4”的左边，最后 需要更新平衡因子的节点是“3”，“4”，“5”；

平衡后的值分别为：0，0，1；

当然也有新节点插在“4”的右边的情况，具体是看“4”节点的平衡因子判断插入情况：

1.平衡因子为-1（在左边插入），旋转后需要更新的节点的值为：0、0、1；

2.平衡因子为1 （在右边插入），旋转后需要更新的节点的值为：-1，0，0；

3.平衡因子为0，（特殊情况）， 旋转后需要更新的节点的值为：0，0，0；

特殊情况：

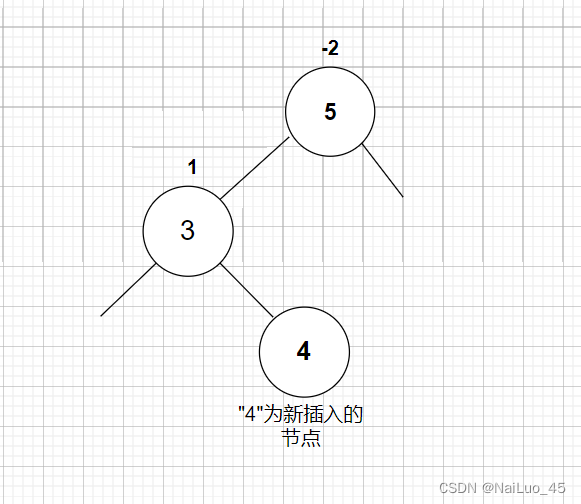
判断条件是父节点平衡因子为-2，左子树平衡因子为1

void RotateLR(Node* parent)
{
	Node* subL = parent->_left;
	Node* subLR = subL->_right;
	int bf = subLR->_bf; //判断平衡因子

	RotateL(parent->_left);
	RotateR(parent);

	subLR->_bf = 0;

	if (bf == 1)
	{
		subL->_bf = -1;
		parent->_bf = 0;
	}
	else if (bf == -1)
	{
		subL->_bf = 0;
		parent->_bf = 1;
	}
	else if (bf == 0)
	{
		subL->_bf = 0;
		parent->_bf = 0;
	}
	else
	{
		assert(false);
	}
}

4.1.4 新节点插入较高右子树的左侧：先右单旋再左单旋

 

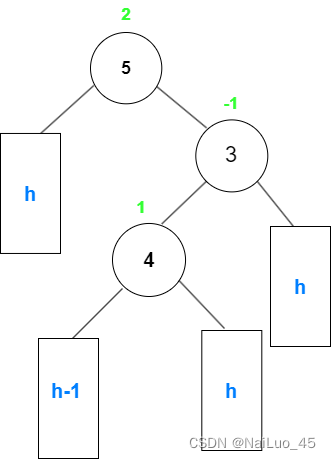
如法炮制： “4”节点右子树插入了一个节点导致整棵树不平衡，“4”这棵树相当于“3”的左子树是较高树的情况，所以对“3”进行右旋；

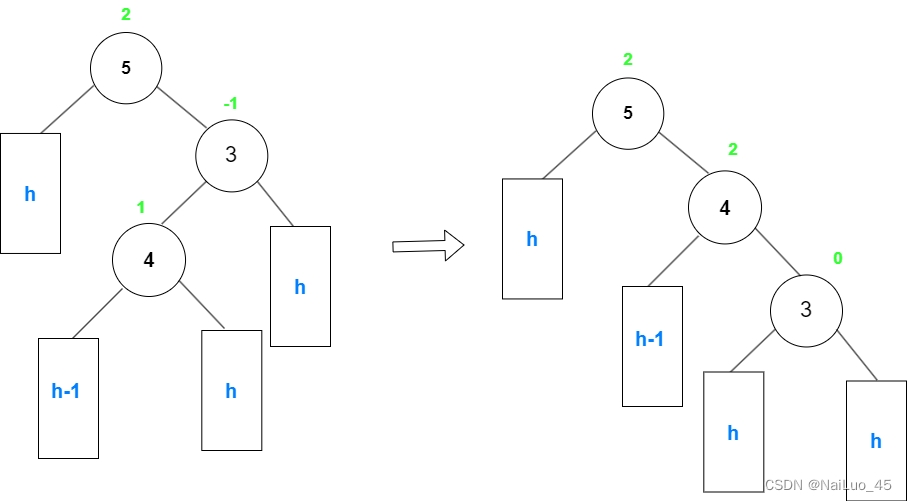
 此时，“3”这棵树相当于 本来是“4”的右子树插入了新节点导致不平衡，应该对“4”进行左单旋。

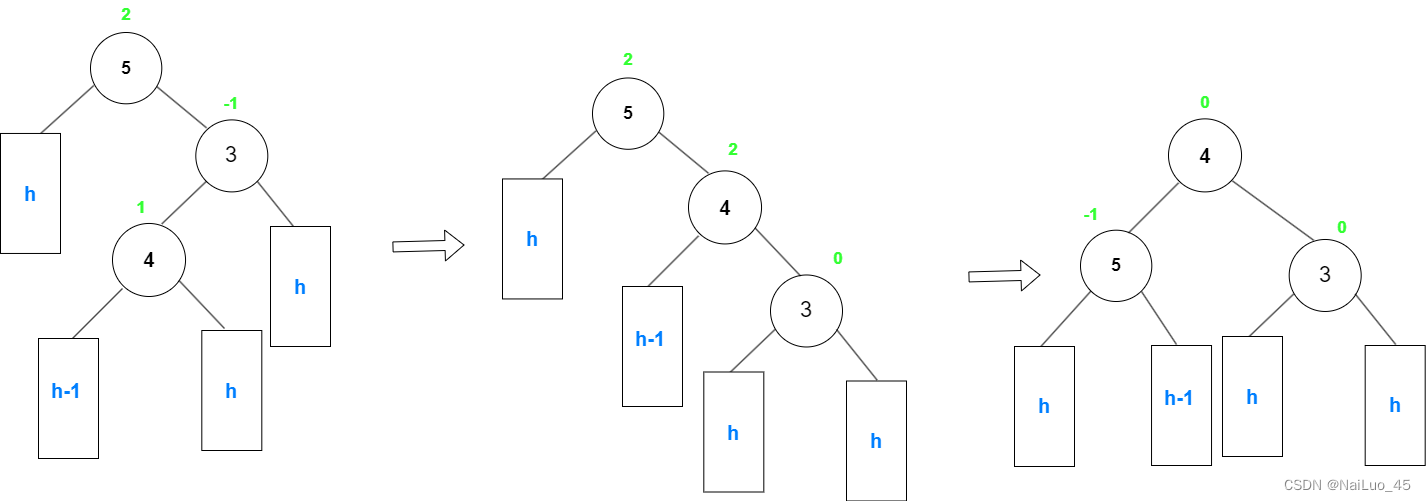
实现代码时，左右旋转只需要复用前面的代码就行，可是双旋完后的平衡因子调节比较麻烦；

上面例子是新节点插在“4”的右边，最后 需要更新平衡因子的节点是“3”，“4”，“5”；

平衡后的值分别为：0，0，-1；

当然也有新节点插在“4”的右边的情况，具体是看“4”节点的平衡因子判断插入情况：

1.平衡因子为-1（在左边插入），旋转后需要更新的节点的值为：1、0、0；

2.平衡因子为1 （在右边插入），旋转后需要更新的节点的值为：0、0、-1；

3.平衡因子为0，（特殊情况）， 旋转后需要更新的节点的值为：0，0，0；

 特殊情况：

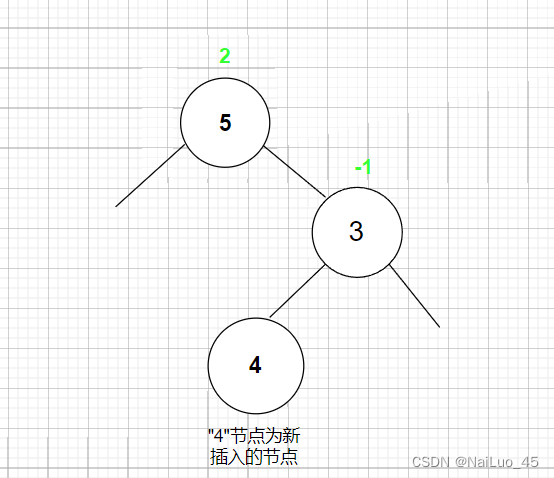
 判断条件是父节点平衡因子为2，左子树平衡因子为-1

void RotateRL(Node* parent)
{
	Node* subR = parent->_right;
	Node* subRL = subR->_left;
	int bf = subRL->_bf;

	RotateR(parent->_right);
	RotateL(parent);

	subRL->_bf = 0;
	if (bf == -1)
	{
		parent->_bf = 0;
		subR->_bf = 1;
	}
	else if (bf == 1)
	{
		parent->_bf = -1;
		subR->_bf = 0;
	}
	else if (bf == 0)
	{
		parent->_bf = 0;
		subR->_bf = 0;
	}
}

 完整代码：

//AVL树节点的定义
template <class K, class V>
struct AVLTreeNode
{
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;
	int _bf;   //平衡因子
	pair<K, V> _kv;

	AVLTreeNode(const pair<K, V>& kv)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_bf(0)
		,_kv(kv)
	{}
};

template <class K, class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:
	bool Insert(const pair<K, V>& kv)   //插入
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);

			return true;
		}

		Node* cur = _root;
		Node* parent = nullptr;

		while (cur)
		{
			if (kv.first > cur->_kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kv.first < cur->_kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else
				return false;
		}

		cur = new Node(kv);
		if (kv.first > parent->_kv.first)
		{
			parent->_right = cur;
		}
		else //(kv.first < parent->_kv.first)
		{
			parent->_left = cur;
		}

		cur->_parent = parent;  

		//更新bf信息
		while (parent)
		{
			//插入节点时，其父节点的平衡因子必定受到影响
			if (cur == parent->_left)
				parent->_bf--;
			else
				parent->_bf++;   

			//根据父节点的平衡因子，看祖先平衡是否被影响
			if (parent->_bf == 0)   
			{
				break;	    //bf 为0，插入并不会引起祖先平衡变化
			}
			else if (parent->_bf == 1 || parent->_bf == -1)  //对于祖先来说，它的子树高度变        
                                                             //化了，会影响平衡
			{
				cur = cur->_parent;
				parent = parent->_parent;    //往上继续更新
			}
			else if (parent->_bf == 2 || parent->_bf == -2)
			{
				//旋转处理
				if (parent->_bf == 2 && cur->_bf == 1)	 //左单旋
				{
					RotateL(parent);
				}
				else if(parent->_bf == -2 && cur->_bf == -1)//右单旋
				{
					RotateR(parent);
				}
				else if (parent->_bf == -2 && cur->_bf == 1) //左右双旋
				{
					RotateLR(parent);	
				}
				else //(parent->_bf == 2 && cur->_bf == -1)	右左双旋
				{
					RotateRL(parent);
				}

				break;
			}
			else   //AVL树再插入之前有问题
			{
				assert(false);
			}

		}

		return true;
	}

	

private:

	void RotateL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;

		parent->_right = subRL;
		if(subRL)
			subRL->_parent = parent;

		Node* ppnode = parent->_parent;
		subR->_left = parent;
		parent->_parent = subR;

		if (_root == parent)
		{
			_root = subR;
			subR->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = subR;
			}
			else
			{
				ppnode->_right = subR;
			}

			subR->_parent = ppnode;
		}

		subR->_bf = 0;
		parent->_bf = 0;
	}

	void RotateR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;

		parent->_left = subLR;
		if (subLR)
			subLR->_parent = parent;

		Node* ppnode = parent->_parent;
		subL->_right = parent;
		parent->_parent = subL;

		if (_root == parent)
		{
			_root = subL;
			subL->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = subL;
			}
			else
			{
				ppnode->_right = subL; 
			}

			subL->_parent = ppnode;
		}

		parent->_bf = 0;
		subL->_bf = 0;
	}

	void RotateLR(Node* parent)
	{
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		int bf = subLR->_bf;

		RotateL(parent->_left);
		RotateR(parent);

		subLR->_bf = 0;

		if (bf == 1)
		{
			subL->_bf = -1;
			parent->_bf = 0;
		}
		else if (bf == -1)
		{
			subL->_bf = 0;
			parent->_bf = 1;
		}
		else if (bf == 0)
		{
			subL->_bf = 0;
			parent->_bf = 0;
		}
		else
		{
			assert(false);
		}
	}

	void RotateRL(Node* parent)
	{
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		int bf = subRL->_bf;

		RotateR(parent->_right);
		RotateL(parent);

		subRL->_bf = 0;
		if (bf == -1)
		{
			parent->_bf = 0;
			subR->_bf = 1;
		}
		else if (bf == 1)
		{
			parent->_bf = -1;
			subR->_bf = 0;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			subR->_bf = 0;
		}
	}

	

	Node* _root = nullptr;
};

 对于AVL树的删除，由于过于复杂，不详细说明；如果以学习为目的去了解AVL树，了解到插入已经足够，没必要完完全全复刻出来！如果你有兴趣或者需要可以自行了解。

 

5.1 AVL树的性能

AVL树是一棵绝对平衡的二叉搜索树，其要求每个节点的左右子树高度差的绝对值都不超过1，这
样可以保证查询时高效的时间复杂度，即 log_2 (N)。
但是如果要对AVL树做一些结构修改的操 作，性能非常低下
比如：插入时要维护其绝对平衡，旋转的次数比较多，更差的是在删除时，
有可能一直要让旋转持续到根的位置。因此：如果需要一种查询高效且有序的数据结构，而且数
据的个数为静态的(即不会改变)，可以考虑AVL树，但一个结构经常修改，就不太适合。

 

感谢浏览！！

NaiLuo_45
关注
C++：AVL树深度剖析
Jdxxwu的博客
11-19 2129
文章讲深度解析AVL树原理与模拟实现，持续更新中. . .
详解AVL树（平衡二叉树）
水澹澹兮生烟
09-20 2万+
插入节点后对树进行旋转调整，分为四种情况。 1.右单旋 当一个平衡二叉树满足具有较高左子树时（如下图A），且要插入的节点插入到了较高左子树的左侧，此时进行右单旋。
【数据结构】AVL树
weixin_74078718的博客
05-12 3372
AVL树的概念、定义、插入、旋转等内容。
【数据结构】AVL树（万字超详细 附动图）
Eristic0618的博客
04-23 1万+
本篇文章围绕数据结构中的AVL树展开讲解，包含AVL树的插入、旋转、验证等内容，万字讲解搭配自制动图
AVL树（动图详解）
2021dragon的博客
12-02 2万+
AVL树（C++实现）
数据结构--AVL树（全）
weixin_48560325的博客
05-01 9520
目录 什么是AVL树？ AVL树的特点及形成原因 二叉搜索树基本概念 二叉搜索的特点 二叉搜索树的优点及缺点 改进的二叉搜索树——AVL树 AVL树的定义 AVL树的特点 结点的平衡因子balance 构建一个AVL树 构建一个AVL树的节点 什么是AVL树？ AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。 AVL树的特点及形成原因 AVL树本质.
C++:AVL树保姆级详解
最新发布
2301_80418172的博客
09-08 1270
AVL树详解
精选资源
AVLComparison:AVL 树的 C++ 和 Haskell 运行时效率比较
07-05
在本项目"AVLComparison:AVL 树的 C++ 和 Haskell 运行时效率比较"中，我们将探讨这两种编程语言实现AVL树的性能差异。 首先，让我们关注C++的实现。C++是一种静态类型的、编译式的、通用的、大小写敏感的、不仅...
C++：AVL树的解析与模拟
Makise的博客
09-04 868
一篇带你完全掌握AVL树
数据结构 —— 图解AVL树(平衡二叉树)
热门推荐
猎人在吃肉
07-28 6万+
文章目录1、AVL树(平衡二叉树)的定义1.1、平衡因子2、AVL树的作用：3、AVL树的基本操作3.1、插入—— 左左型的右旋：3.1.1、右旋的具体步骤：3.1.2、右旋的动画演示：3.1.3、右旋示例：3.2、插入——右右型的左旋：3.2.1、左旋的具体步骤：3.2.2、动画演示：3.2.3、左旋举例：3.3、插入——左右型的左右旋 ( 即先左后右)：3.3.1、左右旋的两次旋转步骤：3.3...
AVL树（平衡二叉搜索树）
langk_的博客
09-03 3822
带你手撕AVL树，左单旋，右单旋，左右双旋，右左双旋
数据结构——AVL树详解
rab1211764820的博客
03-28 5056
AVL树的模拟实现 AVL树的插入、旋转、删除、查找 AVL树的验证 AVL树的平衡因子
AVL树详解
good good study, day day up!
11-09 2057
AVL树、单旋转、双旋转
【数据结构】AVL树(图文解析 + 代码实现)
2301_80277275的博客
07-23 3847
AVL树的概念、AVL树结点的定义、AVL树的插入、AVL树的旋转、AVL树的验证
AVL树-详细解析【数据结构】
m0_73916791的博客
12-17 1291
AVL树保持了二叉查找树的基础性质，即对于任何一个节点，其左子树上的所有节点的值都小于该节点的值，右子树所有节点的值都大于该节点的值。常规情况下，左子树或右子树的高度的计算是从当前节点向下递归到叶子节点，计算最长路径上边的数量，叶子节点的高度定义为0。这是LL的镜像操作，当一个节点N的右子树的右边产生了一个新节点，并造成不平衡时，会进行RR旋转。首先在导致失衡节点的左子树上进行左旋转，然后对该节点进行右旋转。这是LR旋转的镜像，当一个节点N的右子树的左边产生了一个新节点，并造成不平衡时，会进行RL旋转。
评论
成就一亿技术人!
拼手气红包6.0元
还能输入1000个字符
 
红包 添加红包
表情包 插入表情
表情包 代码片
 条评论被折叠 查看
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值