模拟实现二叉树（C语言）

1.二叉树的遍历

遍历如下图所示的二叉树

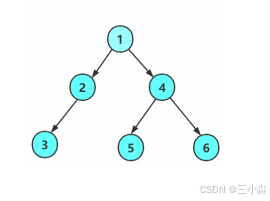
前序遍历

void TreePrevOrder(TreeNode* root)
{
    if (root == NULL)
    {
        printf("N ");
        return;
    }
    printf("%d ", root->x);
    TreePrevOrder(root->left);
    TreePrevOrder(root->right);
}

中序遍历

void TreeInOrder(TreeNode* root)
{
    if (root == NULL)
    {
        printf("N ");
        return;
    }
    TreeInOrder(root->left);
    printf("%d ", root->x);
    TreeInOrder(root->right);
}

 后序遍历

void TreePostOrder(TreeNode* root)
{
    if (root == NULL)
    {
        printf("N ");
        return;
    }
    TreePostOrder(root->left);
    TreePostOrder(root->right);
    printf("%d ", root->x);
}

层序遍历

void TreeLevelOrder(TreeNode* root)
{
    Queue q;
    QueueInit(&q);
    if (root)
    {
        QueuePush(&q,root);
    }
    while (!QueueEmpty(&q))
    {
        TreeNode* front = QueueFront(&q);
        QueuePop(&q);
        printf("%d ", front->x);
        if (front->left)
            QueuePush(&q, front->left);
        if (front->right)
        {
            QueuePush(&q, front->right);
        }
    }
}

程序遍历需要用到队列，先进先出。

如上图所示，先插入根结点1，当1出队列时，他的左右结点进队列，当2出队列时，结点2的左右结点再进队列，依次一层一层遍历。

2.二叉树结点的个数

int TreeSize(TreeNode* root)
{
    if (root == NULL)
    {
        return 0;
    }
    return TreeSize(root->left) + TreeSize(root->right) + 1;
}

上述中，当遇到空指针时，返回0。TreeSize(root->left) + TreeSize(root->right) + 1这句代码是指左子树的结点个数+右子树结点的个数+一个根结点

3.叶子节点的个数

int TreeLeafSize(TreeNode* root)
{
    if (root == NULL)
    {
        return 0;
    }
    if (root->left == NULL && root->right == NULL)
    {
        return 1;
    }
    return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

4.第k层结点的个数

规定根结点为第一层

int TreeLevelKSize(TreeNode* root, int k)
{
    assert(k > 0);
    if (root == NULL)
    {
        return 0;
    }
    if (k == 1)
    {
        return 1;
    }
    return TreeLevelKSize(root->left, k - 1) + TreeLevelKSize(root->right, k - 1);
}

5.二叉树查找值为x的结点

TreeNode* TreeFind(TreeNode* root, TreeDataType x)
{
    if (root == NULL)
    {
        return NULL;
    }
    if (root->x == x)
    {
        return root;
    }
    TreeNode* left = TreeFind(root->left, x);
    if (left->x == x)
    {
        return left;
    }
    TreeNode* right = TreeFind(root->right, x);
    if (right->x == x)
    {
        return right;
    }
    return NULL;

}

6.判断二叉树是否是完全二叉树

int TreeComplete(TreeNode* root)
{
    Queue q;
    QueueInit(&q);
    if (root)
    {
        QueuePush(&q, root);
    }
    while (!QueueEmpty(&q)) 
    {
        TreeNode* front = QueueFront(&q);
        QueuePop(&q);
        if (front == NULL)  //遇到空结点就退出循环
        {
            break;
        }
        QueuePush(&q, front->left);
        QueuePush(&q, front->right);

    }
    while (!QueueEmpty(&q))  //若队列中剩余的结点中，有一个结点不是NULL，就不是完全二叉树
    {
        if (QueueFront(&q))
        {
            return 0;
        }
    }
    return 1;
}

返回值为1则是完全二叉树，返回值为0不是完全二叉树