吴恩达机器学习作业8（上）--- Anomaly Detection（异常检测）

最新推荐文章于 2022-11-04 20:03:03 发布

原创

最新推荐文章于 2022-11-04 20:03:03 发布 · 389 阅读

0 ·

CC 4.0 BY-SA版权

这篇博客介绍了异常检测中的原始模型和多元高斯分布模型，重点在于实现高斯分布函数、估计参数及选择阈值ε。通过训练集和交叉验证集进行模型验证，以F1-score评估最佳阈值。最后，在高维数据集上进行了测试，发现特征间存在相关性影响模型表现。

文章目录

代码分析

前言

异常检测模型分为原始模型和多元高斯分布模型

原始模型为多元高斯分布模型的特例

其区别是

原始模型的协方差矩阵为对角矩阵，其特征相互独立
多元高斯分布模型的特征存在相关性

实现高斯分布函数

首先导入类库

import numpy as np
import matplotlib.pyplot as plt
import scipy.io 
import scipy.optimize #Use for fmincg
%matplotlib inline

导入数据，有训练集（无标签），交叉验证集（有标签）

datafile = 'data/ex8data1.mat'
mat = scipy.io.loadmat( datafile )
#训练集，无标签
X = mat['X']
#交叉验证集，有标签
ycv = mat['yval']
Xcv = mat['Xval']

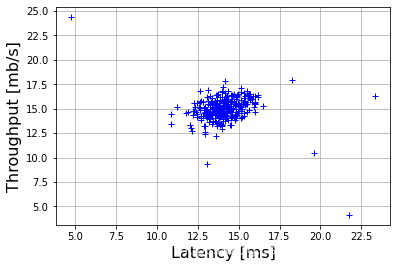
可视化函数

# Visualize the data
def plotData(myX, newFig=False):
    if newFig:
        plt.figure(figsize=(8,6))
    plt.plot(myX[:,0],myX[:,1],'b+')
    plt.xlabel('Latency [ms]',fontsize=16)
    plt.ylabel('Throughput [mb/s]',fontsize=16)
    plt.grid(True)
    
plotData(X)

在这里插入图片描述
下图为多元高斯分布函数

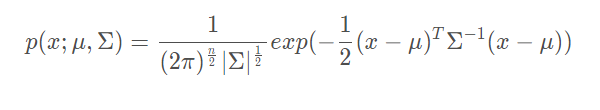
实现高斯分布函数（兼容单变量和多变量）

#此函数得出p方程，兼容原始模型和多元高斯分布模型
def gaus(myX, mymu, mysig2):
    m = myX.shape[0]#数据集个数
    n = myX.shape[1]#特征数
    #如果sigma是向量，就转化为对角矩阵（协方差矩阵）
    if np.ndim(mysig2) == 1:
        mysig2 = np.diag(mysig2)
    #计算常数项
    norm = 1./(np.power((2*np.pi), n/2)*np.sqrt(np.linalg.det(mysig2)))
    myinv = np.linalg.inv(mysig2)#sigma取逆
    myexp = np.