vanilla RNNs和LSTM和GRU公式推导相关

最新推荐文章于 2025-06-20 18:30:51 发布

gyl2016

最新推荐文章于 2025-06-20 18:30:51 发布

阅读量2.2k

点赞数 2

分类专栏：深度学习文章标签：深度学习

深度学习专栏收录该内容

15 篇文章

订阅专栏

本文深入探讨了循环神经网络（RNN）的基本原理，包括vanilla RNNs的结构与工作流程，以及如何通过反向传播算法进行训练。此外，还详细介绍了LSTM网络，一种解决长期依赖问题的有效模型，涵盖了其独特的门控机制，如忘记门、更新门和输出门，以及几种LSTM的变体。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1、 vanilla RNNs

文章转自https://blog.youkuaiyun.com/dchen1993/article/details/53885490

相比于LSTM、GRU，vanilla RNNs 是最简单的循环神经网络。

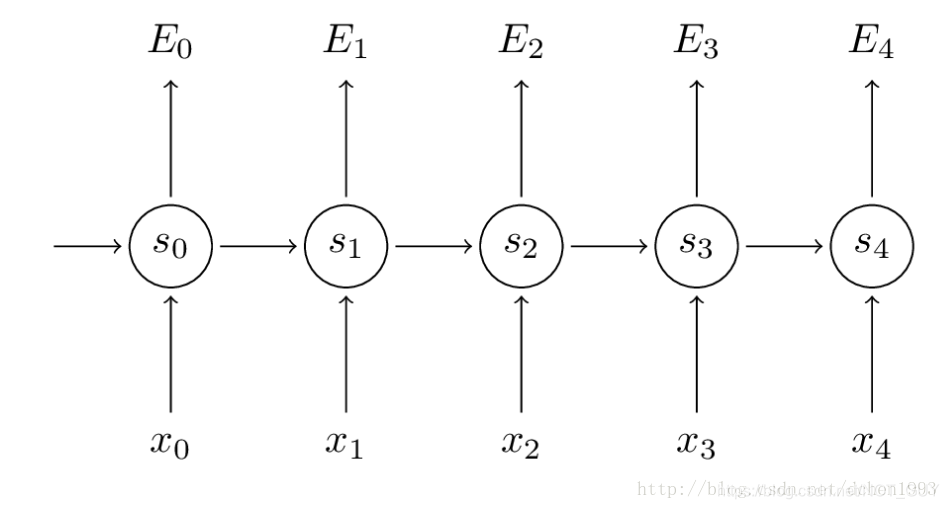
RNN结构

RNN的一个特点是所有隐层共享参数（U, W, V），整个网络只用这一套参数，能大大减少计算量。

RNN前向传导

$s_{t}=f\left ( Ux_{t}+Ws_{t-1} \right )$ ，其中， $f\left ( \cdot \right )$ 可以是sigmoid函数、tanh函数、relu函数；

$o_{t}=softmax(Vs_{t})$

$s_{t}$ 为 t 时刻隐层的状态值，为向量。

$o_{t}$ 为 t 时刻的输出值。上图中，每一个time step都会有一个输出，但是这个不是必要的，可以根据任务而定。例如：（1）如果我们想要预测句子中下一个单词，则 $o_{t}$ 是一个概率向量，该向量的维度是词表大小。（2）当只关心句子的语意信息时，只需要最后一个输出就行了。

RNN后向传播

构造训练数据

构造过程：

1、生成词典vocab。（分词、去掉低频词）

2、将语料中的句子转为word_id序列，并在头尾加上开始和结束符id。

3、生成训练数据：对于每一个句子，输入为前len(sentence)-1的序列，输出为后len(sentence)-1的序列（也就是输入一个词就预测下一个词）。

如：“我在沙滩上玩耍”输入的向量为[0, 5, 85, 485, 416, 55]，输出的向量为[5, 85, 485, 416, 55, 1]。

假如我们的词汇有8000个，采用one-hot向量，则每个输入 $x_{t}$ 为8000维，对应的位置为1，其他为0。

隐层设置100个神经元，则列出网络所有参数和输入输出的shape，方便推导：

$x_{t}\in \mathbb{R}^{8000}$

$o_{t}\in \mathbb{R}^{8000}$

$s_{t}\in \mathbb{R}^{100}$

$U\in \mathbb{R}^{100\times 8000}$

$V\in \mathbb{R}^{8000\times 100}$

$W\in \mathbb{R}^{100\times 100}$

总参数量为 $2HC+H^{2}$ ，即1610000。

损失函数采用交叉熵： $E_{t}\left ( y_{t}, \hat{y}_{t} \right )=- y_{t}log\hat{y}_{t}$ ， $E\left ( y, \hat{y} \right )=\Sigma _{t}E\left ( y_{t}, \hat{y}_{t} \right )=-\Sigma _{t} y_{t}log\hat{y}_{t}$ ，其中 $y_{t}$ 为 t 时刻正确的词语， $\hat{y}_{t}$ 为 t 时刻预测的词语。

求解误差E关于所有参数（U, V, W）的梯度，即 $\frac{\partial E}{\partial U}$ 、 $\frac{\partial E}{\partial V}$ 、 $\frac{\partial E}{\partial W}$ 。

如下图所示，每个时刻 t 预测的词都有相应的误差，我们需要求这些误差关于参数的所有梯度，最后进行参数的下降调整操作（由于目标是降低Loss function，所以是梯度下降，如果目标是最大似然，则为梯度上升）。

这里计算 $E_{3}$ 关于参数的梯度为例（其他 $E_{t}$ 都需要计算）：

$\frac{\partial E_{3}}{\partial V}=\frac{\partial E_{3}}{\partial \hat{y_{3}}}\frac{\partial \hat{y_{3}}}{\partial V} =\frac{\partial E_{3}}{\partial \hat{y_{3}}}\frac{\partial \hat{y_{3}}}{\partial z_{3}}\frac{\partial z_{3}}{\partial V}=\left ( \hat{y_{3}}-y_{3}\right )\times s_{3}$ 为 $8000\times 100$ 的向量，其中 $z_{3}=Vs_{3}$ ，用到了softmax的求导公式。可见关于V的梯度用不到上一层的状态值，所以不需要累计。

BPTT（Backpropagation Through Time）

下面来求解关于W的梯度：

$\frac{\partial E_{3}}{\partial W}=\frac{\partial E_{3}}{\partial \hat{y_{3}}}\frac{\partial \hat{y_{3}}}{\partial s_{3}}\frac{\partial s_{3}}{\partial W}$

由于 $s_{3}=tanh\left ( Ux_{3}+Ws_{2} \right )$ 依赖 $s_{2}$ ，而 $s_{2}$ 依赖W和 $s_{1}$ ，以此类推。

下图为链式关系：

所以，

$\frac{\partial E_{3}}{\partial W}=\sum_{k=0}^{3}\frac{\partial E_{3}}{\partial \hat{y}_{3}}\frac{\partial \hat{y}_{3}}{\partial s_{3}}\frac{\partial s_{3}}{\partial s_{k}}\frac{\partial s_{k}}{\partial W}$

可见由于W在所有隐层中共享，许多变量都依赖W，导致求导链变长，这就是BPTT的特点，将每层的影响都累计起来。

下图为各链接之间的导数，在所有层中不会改变，也体现了传播的路径。

跟一般的反向传播一样，这里也定义一个Delta向量：

$\delta_{2}^{(3)}=\frac{\partial E_{3}}{\partial s_{3}}\frac{\partial s_{3}}{\partial s_{2}}\frac{\partial s_{2}}{\partial z_{2}}$

其中 $z_{2}=Ux_{2}+Ws_{1}$ ，在本例子中为一个 $100\times 1$ 的向量。

所以 $\frac{\partial E_{3}}{\partial W}$ 可以写成：

$\frac{\partial E_{3}}{\partial W}=\sum_{k=0}^{3}\delta _{k}^{(3)}\frac{\partial z_{k}}{\partial W}$ 为 $100\times 100$ 的矩阵。

同理 $\frac{\partial E_{3}}{\partial U}$ 可以写成：

$\frac{\partial E_{3}}{\partial U}=\sum_{k=0}^{3}\delta _{k}^{(3)}\frac{\partial z_{k}}{\partial U}$ 为 $100\times 8000$ 的矩阵。

至此，关于（U, V, W）的梯度都求解完毕。

2、LSTM

文章转自https://www.jianshu.com/p/9dc9f41f0b29

LSTM网络结构

1、忘记门

在我们 LSTM 中的第一步是决定我们会从细胞状态中丢弃什么信息。这个决定通过一个称为忘记门层完成。该门会读取 $h_{t-1}$ 和 x_t ，输出一个在到之间的数值给每个在细胞状态 $C_{t-1}$ 中的数字。表示“完全保留”，表示“完全舍弃”。

2、更新门

下一步是确定什么样的新信息被存放在细胞状态中。这里包含两个部分。第一，sigmoid层称 “输入门层” 决定什么值我们将要更新。然后，一个 tanh 层创建一个新的候选值向量， $\tilde{C}_t$ ，会被加入到状态中。下一步，我们会讲这两个信息来产生对状态的更新。

现在是更新旧细胞状态的时间了， $C_{t-1}$ 更新为 C_t 。前面的步骤已经决定了将会做什么，我们现在就是实际去完成。

我们把旧状态与 f_t 相乘，丢弃掉我们确定需要丢弃的信息。接着加上 $i_t * \tilde{C}_t$ 。这就是新的候选值，根据我们决定更新每个状态的程度进行变化。

3、输出门

最终，我们需要确定输出什么值。这个输出将会基于我们的细胞状态，但是也是一个过滤后的版本。首先，我们运行一个 sigmoid 层来确定细胞状态的哪个部分将输出出去。接着，我们把细胞状态通过 tanh 进行处理（得到一个在到之间的值）并将它和 sigmoid 门的输出相乘，最终我们仅仅会输出我们确定输出的那部分。