PAT甲级 1007 Maximum Subsequence Sum(25) (线性DP)

NHS6671

于 2022-05-06 09:10:14 发布

阅读量219

点赞数 1

CC 4.0 BY-SA版权

分类专栏： PAT-甲级文章标签：动态规划算法 pat考试 c++

本文链接：https://blog.youkuaiyun.com/NHS6671/article/details/124602030

PAT-甲级专栏收录该内容

70 篇文章

订阅专栏

该博客介绍了PAT甲级考试中的一道题，即寻找一个整数序列的最大连续子序列和，并输出该子序列的第一个和最后一个元素。文章通过动态规划方法解析问题，给出状态转移方程`dp[i]=max(dp[i-1]+a[i],a[i])`，并提供了代码实现。在所有元素为负数的情况下，最大子序列和为0，输出整个序列的首尾元素。" 86729250,2116373,机器学习集成方法：随机森林与AdaBoost解析,"['机器学习', '随机森林', '自适应增强', '集成方法']

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目

Given a sequence of K integers { $N_{1}$ , $N_{2}$ , ..., $N_{k}$ }. A continuous subsequence is defined to be { $N_{i}$ , $N_{i+1}$ , ..., $N_{j}$ } where 1≤i≤j≤K. The Maximum Subsequence is the continuous subsequence which has the largest sum of its elements. For example, given sequence { -2, 11, -4, 13, -5, -2 }, its maximum subsequence is { 11, -4, 13 } with the largest sum being 20.

Now you are supposed to find the largest sum, together with the first and the last numbers of the maximum subsequence.

输入

Each input file contains one test case. Each case occupies two lines. The first line contains a positive integer K (≤10000). The second line contains K numbers, separated by a space.

输出

For each test case, output in one line the largest sum, together with the first and the last numbers of the maximum subsequence. The numbers must be separated by one space, but there must be no extra space at the end of a line. In case that the maximum subsequence is not unique, output the one with the smallest indices i and j (as shown by the sample case). If all the K numbers are negative, then its maximum sum is defined to be 0, and you are supposed to output the first and the last numbers of the whole sequence.

样例输入

10
-10 1 2 3 4 -5 -23 3 7 -21

样例输出

10 1 4

题意理解

题意十分简单，就是求连续区间的最大子序列和，然后输出这个区间的左端点的值，右端点的值，如果这个区间的值小于0的话，那么输出0和整个序列的左端点和右端点。

状态分析

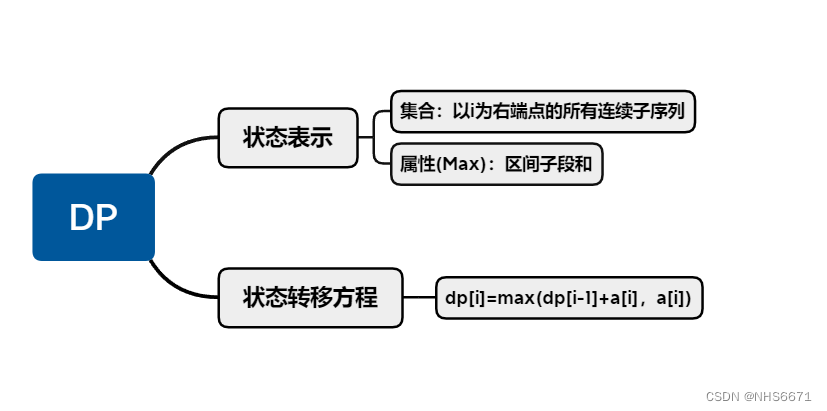
我们的状态划分如上图，那么怎么确定转移方程呢？

将所有集合划分为两种情况

1.集合里面只有一个元素，也就是区间长度为1。

2.集合里面有多个元素，也就是以i为结尾的所有连续区间的子段和。

dp[i-1]表示以i-1为结尾的最大连续区间和，如果加上a[i]这个元素比a[i]更小的话，那么说明前面都是负数，那么我们是可以丢掉前面的负数序列的。

两种集合情况我们取一个Max

此时得到了我们的

状态转移方程

dp[i]=max(dp[i-1]+a[i],a[i])

那么我们得到了状态转移方程之后就要考虑代码实际逻辑，因为我们要输出左端点和右端点的值，那么我们用一个临时左端点变量去保存，只有当前面序列连续和小于0时，我们才去更新左端点，如果当前以i为结尾的区间大于结果的话，我们就更新结果，将右端点变成i，左端点就是我们临时保存的临时左端点，最后判断一下，如果最后结果还是小于0的话，那么就根据题意输出整个序列就好。

注意这里输出的是左右端点的值，不是序号。

代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
const int INF=0x3f3f3f3f;
int n,m;
int a[N],dp[N];
int res=-INF;
int main(){
    
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    
    int l=1,r=1,t=1;
    for(int i=1;i<=n;i++){
       dp[i]=max(dp[i-1]+a[i],a[i]);
       if(dp[i-1]<0)t=i;
       if(res<dp[i]){
           l=t;
           r=i;
           res=dp[i];
       }
    }
    if(res<0){
        l=1,r=n,res=0;
    }
    
    printf("%d %d %d\n",res,a[l],a[r]);
    
    return 0;
}