【算法修炼】图论算法四（SPFA单源最短路径应用及其扩展）

先贴贴模板：

class Solution {
    public int networkDelayTime(int[][] times, int n, int k) {
        // 先建图
        List<int[]>[] graph = new LinkedList[n + 1];
//         也可以写成：
//        List<Integer>[] graph = new LinkedList[n];
        // List数组记得对每一个List进行初始化，才能使用
        // 注意节点从1开始，数组大小要开成：n + 1
        for (int i = 1; i <= n; i++) {
            graph[i] = new LinkedList<>();
        }
        for (int[] time : times) {
            int from = time[0];
            int to = time[1];
            int weight = time[2];
            // from -> List<(to, weight)>
            // 邻接表存储图结构，同时存储权重信息weight
            graph[from].add(new int[]{to, weight});
        }
        // 记录开始节点到任一节点的最短路径
        int[] distTo = new int[graph.length];
        Arrays.fill(distTo, Integer.MAX_VALUE);
        // 记录是否入队
        boolean[] vis = new boolean[graph.length];
        // 统计当前节点的遍历次数，用于判断负环
        int[] nums = new int[graph.length];
        // 初始条件
        distTo[k] = 0;
        vis[k] = true;
        // 只有一个点，不含边
        nums[k] = 0;
        // 是否为负环
        boolean flag = false;
        // SPFA开始，k为起点
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(k);
        while (!queue.isEmpty()) {
            int curId = queue.poll();
            // 出队，与BFS题目的vis数组区分开
            vis[curId] = false;
            // 遍历与该节点相邻的节点
            for (int[] next : graph[curId]) {
                int nextId = next[0];
                int weight = next[1];
                // 如果当前的更新距离更小才能更新
                if (distTo[nextId] > distTo[curId] + weight) {
                    // 更新距离
                    distTo[nextId] = distTo[curId] + weight;
                    // 当前节点的最短路径包含的边数 + 1
                    nums[nextId] = nums[curId] + 1;
                    if (nums[nextId] == n) {
                        // 是负环
                        flag = true;
                        break;
                    }
                    // 如果队列中没有，就入队
                    if (vis[nextId] == false) {
                        vis[nextId] = true;
                        queue.offer(nextId);
                    }
                }
            }
            // 是负环
            if (flag) {
                break;
            }
        }
        // 是负环了
        if (flag) {
            return -1;
        }
        int res = 0;
        for (int i = 1; i < graph.length; i++) {
            if (distTo[i] == Integer.MAX_VALUE) {
                return -1;
            }
            res = Math.max(res, distTo[i]);
        }
        return res;
    }
}

注意上面的vis数组位置和值，我们将节点拿出来时，vis置为false，是因为vis记录的是当前节点是否在队列中，而BFS搜索中，vis记录的是当前节点是否访问，不是它是不是在队列中，两者不能混淆！

最小体力消耗路径（中等）

把矩阵中的一个个元素，转换为图中的点，注意最短路径的定义：这条路径上高度差绝对值的最大值！

class node {
    int x, y;
    node() {}
    node(int x, int y) {
        this.x = x;
        this.y = y;
    }
}
class Solution {
    public int minimumEffortPath(int[][] heights) {
        int m = heights.length;
        int n = heights[0].length;
        Queue<node> queue = new LinkedList<>();
        // 从(0,0)开始
        queue.offer(new node(0, 0));
        int[][] dist = new int[m][n];
        for (int i = 0; i < m; i++) {
            Arrays.fill(dist[i], 0x3f3f3f3f);
        }
        dist[0][0] = 0;
        // 记录是否入队
        boolean[][] vis = new boolean[m][n];
        vis[0][0] = true;
        // 移动方位
        int[] x = new int[] {0,0,1,-1};
        int[] y = new int[] {1,-1,0,0};
        while (!queue.isEmpty()) {
            node u = queue.poll();
            // 出队修改vis
            vis[u.x][u.y] = false;
            // 存储当前点可能的边
            List<int[]> edges = new LinkedList<>();
            // 遍历可能的四个方向
            for (int i = 0; i < 4; i++) {
                int tx = u.x + x[i];
                int ty = u.y + y[i];
                if (tx < 0 || ty < 0 || tx >= m || ty >= n) continue;
                int w = Math.abs(heights[u.x][u.y] - heights[tx][ty]);
                edges.add(new int[] {tx, ty, w});  // 记录x、y坐标及其路径权值
            }
            // 遍历可能的边
            for (int[] next : edges) {
                int tx = next[0];
                int ty = next[1];
                int w = next[2];
                // 一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的
                int curMin = Math.max(dist[u.x][u.y], w);
                // 那么就需要记录：整个路径上的abs(高度差) 的最大值
                if (dist[tx][ty] > curMin) {
                    dist[tx][ty] = curMin;
                    if (vis[tx][ty] == false) {
                        queue.offer(new node(tx, ty));
                        vis[tx][ty] = true;
                    }
                }
            }
        }
        return dist[m - 1][n - 1];
    }
}

这道题用Dijkstra + 优先队列，可以很快解出来，这里还是用的SPFA。其实Dijkstra代码和SPFA差不多，Dijkstra需要用优先队列，不需要使用vis数组，只需要判断如果能够更新，才入队，否则就不入队，Dijkstra由于使用了优先队列，可以在队列的遍历的过程中提前返回答案（因为优先队列保证了第一次到达终点的答案一定是最小答案，也正是因为用了优先队列，Dijkstra才能那么快）。

SPFA和Dijkstra的过程都有点像DP算法，特别是在更新最值，存储最值时，和dp table一样。

下面给出Dijkstra代码，就是在SPFA基础上改动的：

class Solution {
    int m, n;
    int[] xx = new int[] {1,-1,0,0};
    int[] yy = new int[] {0,0,1,-1};
    public int minimumEffortPath(int[][] heights) {
        m = heights.length;
        n = heights[0].length;
        // 答案数组
        int[][] minTo = new int[m][n];
        for (int i = 0; i < m; i++) {
            Arrays.fill(minTo[i], Integer.MAX_VALUE);
        }
        minTo[0][0] = 0;
        class node {
            int x, y, minDist;
            node (int x, int y, int minDist) {
                this.x = x;
                this.y = y;
                this.minDist = minDist;
            }
        }
        Queue<node> queue = new PriorityQueue<>(new Comparator<node>() {
            @Override
            public int compare(node o1, node o2) {
                return o1.minDist - o2.minDist;
            }
        });
        queue.offer(new node(0,0, 0));
        while (!queue.isEmpty()) {
            node tmp = queue.poll();
            // Dijkstra可以提前结束
            if (tmp.x == m - 1 && tmp.y == n - 1) {
                return tmp.minDist;
            }
            if (tmp.minDist < minTo[tmp.x][tmp.y]) {
                continue;
            }
            for (int[] next : makeGraph(heights, tmp.x, tmp.y)) {
                int tx = next[0];
                int ty = next[1];
                int curMin = Math.max(minTo[tmp.x][tmp.y], Math.abs(heights[tmp.x][tmp.y] - heights[tx][ty]));
                if (curMin < minTo[tx][ty]) {
                    minTo[tx][ty] = curMin;
                    queue.offer(new node(tx, ty, minTo[tx][ty]));
                }
            }
        }
        return minTo[m - 1][n - 1];
    }
    List<int[]> makeGraph(int[][] heights, int x, int y) {
        List<int[]> graph = new LinkedList<>();
        for (int i = 0; i < 4; i++) {
            int tmpx = x + xx[i];
            int tmpy = y + yy[i];
            if (tmpx < 0 || tmpx >= m || tmpy < 0 || tmpy >= n) continue;
            graph.add(new int[] {tmpx, tmpy});
        }
        return graph;
    }
}

概率最大的路径（中等）

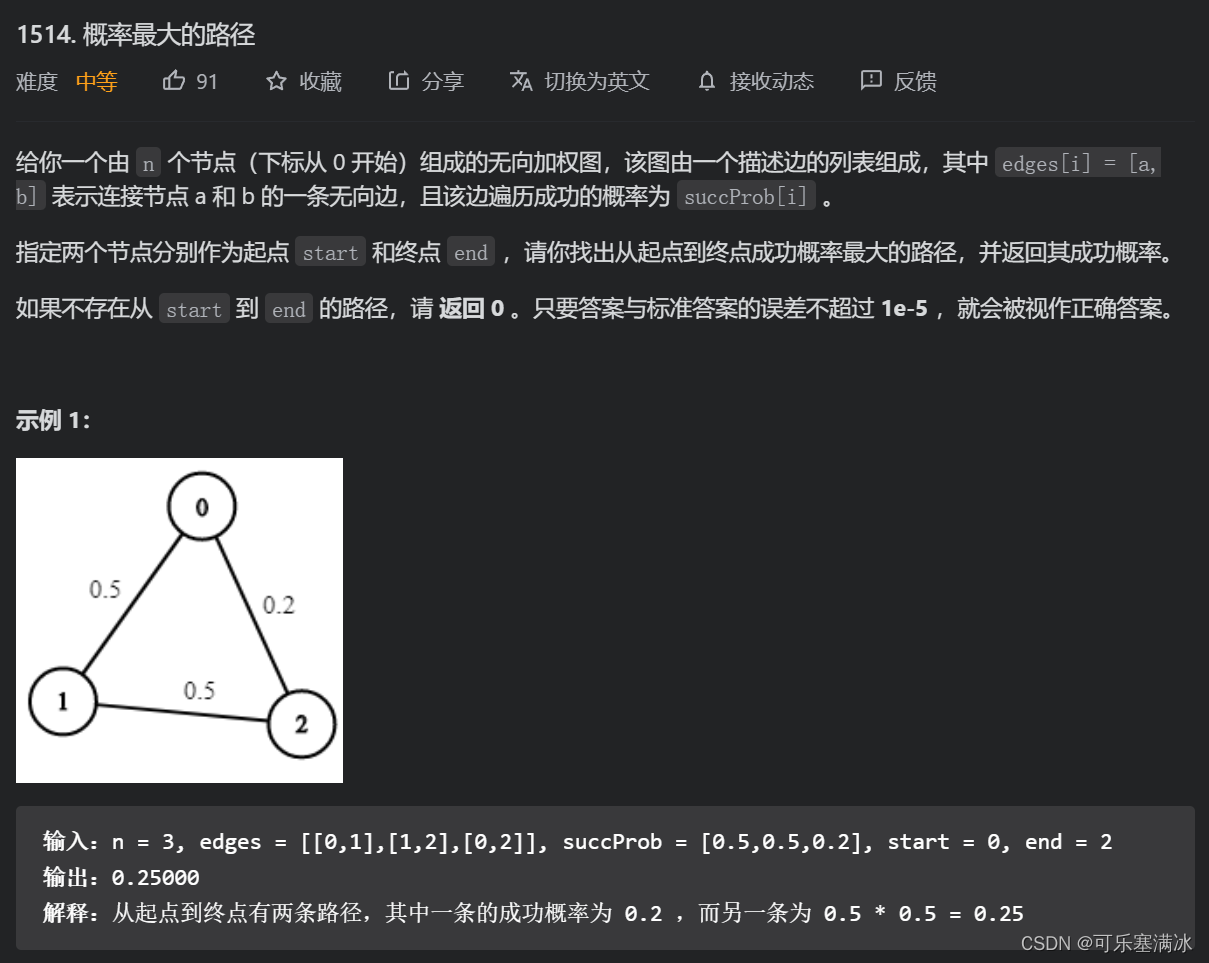
之前一直在说最小路径、有向图，这道题，无向图，求最大值。无向图简单，就是把一条边存两次，求最大值也简单，改变下if判断条件，就Ok啦~。

鸡汤来咯~

class Solution {
    public double maxProbability(int n, int[][] edges, double[] succProb, int start, int end) {
        // 建图，节点下标从0开始
        List<double[]>[] graph = new LinkedList[n];
        for (int i = 0; i < n; i++) {
            graph[i] = new LinkedList<>();
        }
        for (int i = 0; i < edges.length; i++) {
            // 无向图嘛，换个理解方式：双向图~
            graph[edges[i][0]].add(new double[] {edges[i][1], succProb[i]});
            graph[edges[i][1]].add(new double[] {edges[i][0], succProb[i]});
        }
        // 记录结果的数组
        double[] maxProb = new double[n];
        // 找最大值，要初始化为最小值
        Arrays.fill(maxProb, Double.MIN_VALUE);
        // 起点的概率应该是1，不然后续乘权值的时候会报错
        maxProb[start] = 1;
        // 记录是否入队
        boolean[] vis = new boolean[n];
        vis[start] = true;
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(start);
        while (!queue.isEmpty()) {
            int curId = queue.poll();
            vis[curId] = false;
            for (double[] next : graph[curId]) {
                int to = (int)next[0];
                double prob = next[1];
                if (maxProb[to] < maxProb[curId] * prob) {
                    maxProb[to] = maxProb[curId] * prob;
                    if (vis[to] == false) {
                        vis[to] = true;
                        queue.offer(to);
                    }
                }
            }
        }
        // 有可能无法到达
        return maxProb[end] == Double.MIN_VALUE ? 0.00000 : maxProb[end];
    }
}

3488 最短路径（上交机试题）

这题骚在路径长度的把握，因为后面的一条道路的长度一定大于前面的路径总和，所以需要用并查集
在保证起点到其它城市都连通的情况下，道路长度最短，在此基础上再求最短路径，妙哉妙哉！

import java.util.*;
import java.io.*;

class UF {
    // 连通分量个数
    int count;
    // 记录每棵树
    int[] parent;
    // 记录每棵树的大小
    int[] size;
    // 初始化
    UF(int n) {
        this.count = n;
        this.parent = new int[n];
        this.size = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            size[i] = 1;
        }
    }
    // find
    public int find(int x) {
        // 路径压缩
        while (x != parent[x]) {
            parent[x] = parent[parent[x]];
            x = parent[x];
        }
        return x;
    }
    // connected
    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }
    // 联通
    public void union(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        // 已经联通
        if (rootP == rootQ) return;
        // 小树接在大树下
        if (size[rootP] > size[rootQ]) {
            parent[rootQ] = rootP;
            size[rootP] += size[rootQ];
        } else {
            parent[rootP] = rootQ;
            size[rootQ] += size[rootP];
        }
        // 连通分量--
        count--;
    }
    // 查询
    public int count() {
        return count;
    }
}
public class Main {
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
    static BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
    static int MOD = 100000;
    public static void main(String[] args) throws IOException {
        String[] input = reader.readLine().trim().split(" ");
        int n = Integer.parseInt(input[0]);
        int m = Integer.parseInt(input[1]);
        // n个城市下标从0 - n-1
        List<long[]>[] graph = new LinkedList[n];
        for (int i = 0; i < n; i++) {
            graph[i] = new LinkedList<>();
        }
        UF uf = new UF(n);  // n个城市下标从0 - n-1
        for (int i = 0; i < m; i++) {
            input = reader.readLine().trim().split(" ");
            int u = Integer.parseInt(input[0]);
            int v = Integer.parseInt(input[1]);
            // 如果已经联通，那就不用再联通了，后面的道路长度一定大于前面的道路总和
            if (uf.connected(u, v)) continue;
            // 联通
            uf.union(u, v);
            // 算路径长
            long wei = quickPow(2, i);
            // 双向边
            graph[u].add(new long[] {v, wei});
            graph[v].add(new long[] {u, wei});
        }
        // 记录节点路径长
        long[] distTo = new long[n];
        Arrays.fill(distTo, Long.MAX_VALUE);
        distTo[0] = 0;  // 起点=0
        // 是否入队
        boolean[] vis = new boolean[n];
        vis[0] = true;
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(0);
        while (!queue.isEmpty()) {
            int cur = queue.poll();
            vis[cur] = false;  // 出队
            for (long[] next: graph[cur]) {
                int nextId = (int)next[0];
                long wei = next[1];
                if (distTo[nextId] > distTo[cur] + wei) {
                    distTo[nextId] = distTo[cur] + wei;
                    if (vis[nextId] == false) {
                        vis[nextId] = true;
                        queue.offer(nextId);
                    }
                }
            }
        }
        for (int i = 1; i < n; i++) {
            if (distTo[i] == Long.MAX_VALUE) {
                writer.write(-1 + "\n");
            } else {
                // 在最后打印结果时才取模
                writer.write(distTo[i] % MOD + "\n");
            }
        }
        writer.flush();
    }
    // 快速幂
    // 底数、幂
    static long quickPow(long num, long n) {
        if (n == 0) return 1;
        else if (n % 2 == 1) {
            // 奇数
            return quickPow(num, n - 1) * num % MOD;
        } else {
            // 偶数
            long tmp = quickPow(num, n / 2) % MOD;
            return tmp * tmp % MOD;
        }
    }
}

1127 香甜的黄油

要找到所有牛到达的路程和最短的牧场，那就先要以每个牧场为起点，得到其它牧场到该起点的最短距离，得到后，再根据每个牛所在的牧场号与当前牧场号的最短距离求总和，注意，可能牛所在牧场与当前牧场间没有路径，那这个牧场就不用考虑。然后就是求全局的最短距离。

import java.util.*;
import java.io.*;
import java.util.List;

public class Main {
    static BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
    public static void main(String[] args) throws IOException {
        String[] input = reader.readLine().trim().split(" ");
        int n = Integer.parseInt(input[0]);
        int p = Integer.parseInt(input[1]);
        int c = Integer.parseInt(input[2]);
        int[] id = new int[n + 1];
        for (int i = 0; i < n; i++) {
            id[i] = Integer.parseInt(reader.readLine().trim());
        }
        // 建图
        List<int[]>[] graph = new LinkedList[p + 1];
        for (int i = 0; i < p + 1; i++) {
            graph[i] = new LinkedList<>();
        }
        while (c-- > 0) {
            input = reader.readLine().trim().split(" ");
            int A = Integer.parseInt(input[0]);
            int B = Integer.parseInt(input[1]);
            int D = Integer.parseInt(input[2]);
            // 双向边
            graph[A].add(new int[] {B, D});
            graph[B].add(new int[] {A, D});
        }
        // 以每个牧场为起点，得到起点牧场到达其它牧场的最短距离
        // 并记录奶牛的最小距离和
        int ans = 0x3f3f3f3f;
        for (int i = 1; i <= p; i++) {
            Queue<Integer> queue = new LinkedList<>();
            queue.offer(i);
            boolean[] vis = new boolean[p + 1];
            vis[i] = true;
            int[] dist = new int[p + 1];
            Arrays.fill(dist, 0x3f3f3f3f);
            dist[i] = 0;
            while (!queue.isEmpty()) {
                int u = queue.poll();
                vis[u] = false;  // 出队标记为false
                for (int[] next : graph[u]) {
                    int v = next[0];
                    int w = next[1];
                    if (dist[v] > dist[u] + w) {
                        dist[v] = dist[u] + w;
                        if (vis[v] == false) {
                            vis[v] = true;
                            queue.offer(v);
                        }
                    }
                }
            }
            // 求各牛距离和
            int sum = 0;
            for (int j = 0; j < n; j++) {
                int cur = id[j];
                if (dist[cur] == 0x3f3f3f3f) {
                    sum = 0x3f3f3f3f;
                    break;
                }
                sum += dist[cur];
            }
            ans = Math.min(ans, sum);
        }
        System.out.println(ans);
    }
}

920 最优乘车

以输入样例为例：

第一条线路：6 > 7
第二条线路：4 > 7 > 3 > 6
第三条线路：2 > 1 > 3 > 5

从1 > 7，最少转车次数 = 2，1 > 3 > 6 > 7。

本题的关键在于建图，怎么建图？
我们把：同一条线路上的车站之间的权值定义为1，同一条线路上的车站之间都无需转车（单向情况下），如果需要达到的下一车站位于另一条线路，这时就需要转车，转车次数+1，也就是加权值。

import java.util.*;
import java.io.*;
import java.util.List;

public class Main {
    static BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
    public static void main(String[] args) throws IOException {
        String[] input = reader.readLine().trim().split(" ");
        int m = Integer.parseInt(input[0]);
        int n = Integer.parseInt(input[1]);
        // 建图
        List<int[]>[] graph = new LinkedList[n + 1];
        for (int i = 0; i < n + 1; i++) graph[i] = new LinkedList<>();
        // m条巴士线路 n个车站
        for (int i = 1; i <= m; i++) {
            input = reader.readLine().trim().split(" ");
            int len = input.length;
            for (int j = 0; j < len; j++) {
                for (int k = j + 1; k < len; k++) {
                    // 处于同一巴士线路，权重=1，单向
                    int u = Integer.parseInt(input[j]);
                    int v = Integer.parseInt(input[k]);
                    graph[u].add(new int[] {v, 1});
                }
            }
        }
        // SPFA
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(1);  // 起点=1
        boolean[] vis = new boolean[n + 1];
        vis[1] = true;  // 是否入队
        int[] dist = new int[n + 1];  // 最短距离
        Arrays.fill(dist, 0x3f3f3f3f);
        dist[1] = 0;
        while (!queue.isEmpty()) {
            int u = queue.poll();
            // 一定要记得出队清除标记
            for (int[] next : graph[u]) {
                int v = next[0];
                int w = next[1];
                if (dist[v] > dist[u] + w) {
                    dist[v] = dist[u] + w;
                    if (vis[v] == false) {
                        vis[v] = true;
                        queue.offer(v);
                    }
                }
            }
        }
        System.out.println(dist[n] == 0x3f3f3f3f ? -1 : dist[n] - 1);
    }
}

903 昂贵的聘礼（超级源点 + 等级范围限制）

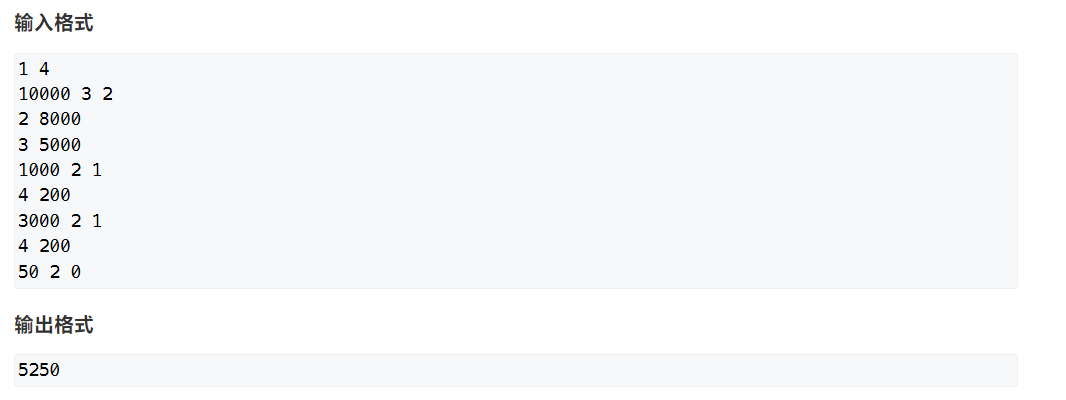
关键点：

• 超级源点
• 替换物品就是增加一个节点到达原物品
• 存在等级区间，必须要在酋长等级的基础上考虑等级区间

import java.util.*;
import java.io.*;
import java.util.List;

public class Main {
    static BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
    public static void main(String[] args) throws IOException {
        String[] input = reader.readLine().trim().split(" ");
        int m = Integer.parseInt(input[0]);
        int n = Integer.parseInt(input[1]);
        // 记录每个物品的阶级
        int[] level = new int[n + 1];
        // 以每个物品为节点建图
        List<int[]>[] graph = new LinkedList[n + 1];
        for (int i = 0; i < n + 1; i++) graph[i] = new LinkedList<>();
        for (int i = 1; i <= n; i++) {
            input = reader.readLine().trim().split(" ");
            int price = Integer.parseInt(input[0]);
            int le = Integer.parseInt(input[1]);
            level[i] = le;
            int cnt = Integer.parseInt(input[2]);
            // 添加一个零号节点，表示直接购买该物品所需要的金币数
            graph[0].add(new int[] {i, price});
            // 遍历可能的替代品
            while (cnt-- > 0) {
                input = reader.readLine().trim().split(" ");
                int t = Integer.parseInt(input[0]);  // 替代品编号
                int v = Integer.parseInt(input[1]);  // 优惠价格
                // 以替代品为节点建边到第i号物品，权值为v
                graph[t].add(new int[] {i, v});
            }
        }
        int ans = 0x3f3f3f3f;
        // 枚举可能的等级范围,因为外来人刚进来不受任何限制,限制是从购买的第一份物品开始
        for (int i = level[1] - m; i <= level[1]; i++) {
            // 必须要以level[1]为基准进行限制，因为最后必须要到达level[1]
            // 可以和[i, i + m]区间的人交易
            int res = spfa(i, i + m, graph, level);
            ans = Math.min(ans, res);
        }
        System.out.println(ans);
    }
    // left、right对等级进行限制的spfa
    static int spfa(int left, int right, List<int[]>[] graph, int[] level) {
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(0);  // 从超级节点0开始
        boolean[] vis = new boolean[graph.length];
        vis[0] = true;  // 入队
        int[] dist = new int[graph.length];
        Arrays.fill(dist, 0x3f3f3f3f);
        dist[0] = 0;
        while (!queue.isEmpty()) {
            int u = queue.poll();
            vis[u] = false;  // 出队置false
            for (int[] next : graph[u]) {
                int v = next[0];
                int w = next[1];
                // 添加了边界限制的spfa
                if (level[v] >= left && level[v] <= right && dist[v] > dist[u] + w) {
                    dist[v] = dist[u] + w;
                    if (vis[v] == false) {
                        queue.offer(v);
                        vis[v] = true;
                    }
                }
            }
        }
        // 最终是为了酋长的女儿!
        return dist[1];
    }
}

1135 新年好（SPFA单源最短路 + DFS全排列）

问题在于如何处理：5个亲戚的访问，拜访每个亲戚，但顺序可以任意，也就是说这5个亲戚的访问顺序是一种排列关系，访问顺序必须从佳佳开始，然后访问完所有亲戚即可。

• 可以先计算出，包括佳佳、5个亲戚在内的六个节点到另外六个节点的最短距离，用一个二维数组存储
• 用dfs生成所有可能的5个亲戚的排列顺序，然后根据之前生成的二维数组，索引相应最短距离，求累加和，再求全局最小值即可

import java.util.*;
import java.io.*;
import java.util.List;

public class Main {
    static BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
    static LinkedList<Integer> tmp = new LinkedList<>();
    static boolean[] vis_dfs;
    static int result = 0x3f3f3f3f;  // 记录全局最终答案
    public static void main(String[] args) throws IOException {
        String[] input = reader.readLine().trim().split(" ");
        int n = Integer.parseInt(input[0]);
        int m = Integer.parseInt(input[1]);
        int[] des = new int[6];
        vis_dfs = new boolean[6];  // 用于dfs求全排列
        input = reader.readLine().trim().split(" ");
        for (int i = 1; i <= 5; i++) des[i] = Integer.parseInt(input[i - 1]);
        // 第0号位置存佳佳位置
        des[0] = 1;
        // 建图
        List<int[]>[] graph = new LinkedList[n + 1];
        for (int i = 0; i < n + 1; i++) graph[i] = new LinkedList<>();
        while (m-- > 0) {
            input =  reader.readLine().trim().split(" ");
            int x = Integer.parseInt(input[0]);
            int y = Integer.parseInt(input[1]);
            int t = Integer.parseInt(input[2]);
            // 双向公路
            graph[x].add(new int[] {y, t});
            graph[y].add(new int[] {x, t});
        }
        // 拜访每个亲戚（顺序任意），给他们送去节日的祝福。怎样走，才需要最少的时间？
        // 预先处理以佳佳、5个亲戚，共六个点，每一个点出发到其余点的最短距离
        // 用二维表进行存储
        int[][] dist = new int[7][7];
        // 佳佳是1号点
        for (int i = 0; i < 6; i++) {
            int[] ans = new int[n + 2];
            ans = spfa(des[i], graph);
            // 5个亲戚 + 佳佳自己
            for (int j = 0; j < 6; j++) {
                if (i == j) {
                    dist[i][j] = 0;
                    continue;
                }
                // 以第i个亲戚为起点，到达另外几个亲戚j的最短距离
                dist[i][j] = ans[des[j]];
            }
        }
        // dfs搜索5个亲戚可能的排列，然后统计时间总和，并比较得到全局最小值
        dfs(des, dist);
        System.out.println(result);
    }
    static void dfs(int[] des, int[][] dist) {
        if (tmp.size() == 5) {
            // 找到了当前一个可能的排列方式
            int ans = 0;
            int u = 0;  // 必须从1号车站，对应下标=0开始
            int v = 0;
            // tmp中存的是亲戚的下标
            for (int i = 0; i < 5; i++) {
                v = tmp.get(i);
                ans += dist[u][v];
                u = v;
                if (ans >= 0x3f3f3f3f) break;
            }
            result = Math.min(result, ans);
        }
        for (int i = 1; i <= 5; i++) {
            if (vis_dfs[i]) continue;
            vis_dfs[i] = true;
            tmp.add(i);
            dfs(des, dist);
            // 回溯
            vis_dfs[i] = false;
            tmp.removeLast();
        }
    }
    static int[] spfa(int st, List<int[]>[] graph) {
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(st);
        boolean[] vis = new boolean[graph.length];
        vis[st] = true;
        int[] dist = new int[graph.length];
        Arrays.fill(dist, 0x3f3f3f3f);
        dist[st] = 0;
        while (!queue.isEmpty()) {
            int u = queue.poll();
            // 出队置false
            vis[u] = false;
            for (int[] next : graph[u]) {
                int v = next[0];
                int w = next[1];
                if (dist[v] > dist[u] + w) {
                    dist[v] = dist[u] + w;
                    if (vis[v] == false) {
                        vis[v] = true;
                        queue.offer(v);
                    }
                }
            }
        }
        return dist;
    }
}

※340 通信线路（二分答案 + 边选取）

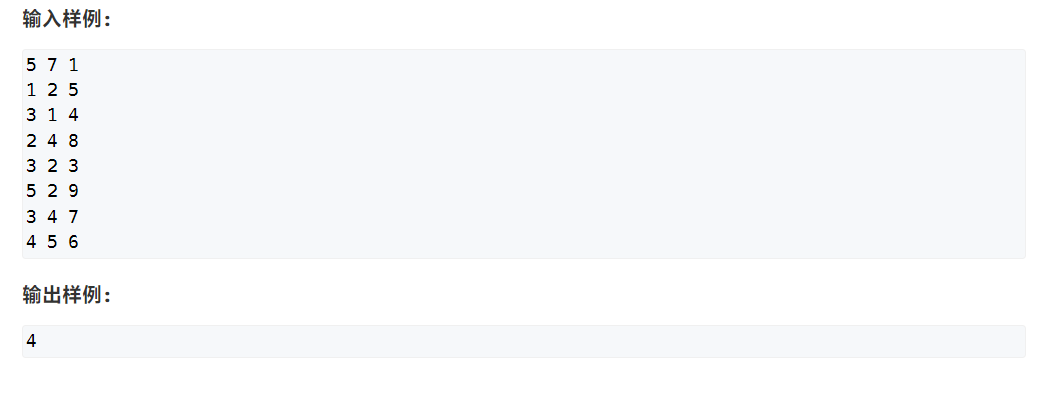
转换下题目含义：将电缆花费从大到小排序，找第k+1大的花费。

对答案二分，然后用spfa求最短路，如果电缆升级花费 > 当前二分结果w，则该电缆（边）的权值=1，否则权值=0，这样求得的最短路径结果dist[n]，就是通信基站 i -> n的路径上的边超过w的条数。

• 如果超过w的条数 > k，说明w太小了，要提高w
• 如果超过w的条数 <= k，说明当前的w是满足的，但为了达到更小的花费，可以试图降低w，注意：试图降低！

---

---

import java.util.*;
import java.io.*;
import java.util.List;

public class Main {
    static BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
    public static void main(String[] args) throws IOException {
        String[] input = reader.readLine().trim().split(" ");
        int n = Integer.parseInt(input[0]);
        int p = Integer.parseInt(input[1]);
        int k = Integer.parseInt(input[2]);
        // 建图
        List<int[]>[] graph = new LinkedList[n + 1];
        for (int i = 0; i < n + 1; i++) graph[i] = new LinkedList<>();
        while (p-- > 0) {
            input = reader.readLine().trim().split(" ");
            int a = Integer.parseInt(input[0]);
            int b = Integer.parseInt(input[1]);
            int l = Integer.parseInt(input[2]);
            graph[a].add(new int[] {b, l});
            graph[b].add(new int[] {a, l});
        }
        // 二分答案,注意左右边界如果要取到一定要多给一点
        int left = 0;
        int right = 1000000 + 1;
        int mid = 0;
        boolean flag = false;
        while (left < right) {
            mid = left + (right - left) / 2;
            if (check(mid, graph, k)) {
                // 尝试让mid更小
                flag = true;
                right = mid;
            } else {
                // mid太小了
                left = mid + 1;
            }
        }
        if (flag == false) {
            // 不存在路径
            System.out.println(-1);
        } else {
            System.out.println(right);
        }
    }
    // 以当前的二分结果做spfa
    static boolean check(int mid, List<int[]>[] graph, int k) {
        Queue<Integer> queue = new LinkedList<>();
        queue.offer(1);
        boolean[] vis = new boolean[graph.length];
        vis[1] = true;
        int[] dist = new int[graph.length];
        Arrays.fill(dist, 0x3f3f3f3f);
        dist[1] = 0;
        while (!queue.isEmpty()) {
            int u = queue.poll();
            vis[u] = false;  // 出队标记为false
            for (int[] next : graph[u]) {
                int v = next[0];
                int w = next[1];
                // 只有当前边的权值 > mid其权值才能算1
                w = w > mid ? 1 : 0;
                if (dist[v] > dist[u] + w) {
                    dist[v] = dist[u] + w;
                    if (vis[v] == false) {
                        vis[v] = true;
                        queue.offer(v);
                    }
                }
            }
        }
        // 超过mid的边数，最大为k条
        return dist[graph.length - 1] <= k;
    }
}

342 道路与航线（负权值求最短路径）

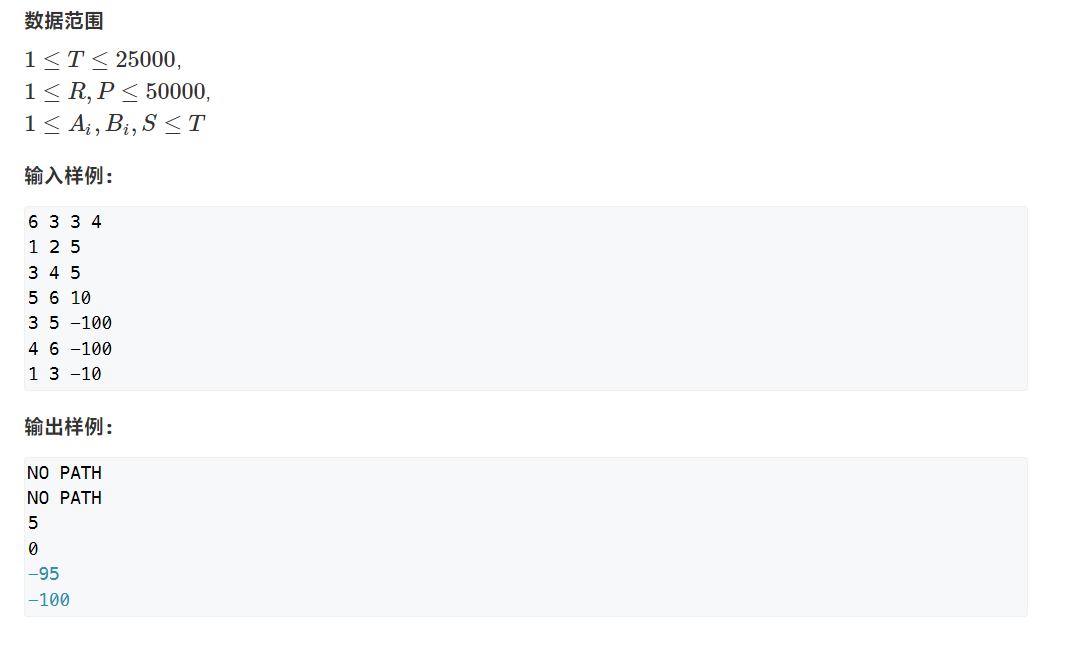
带负权值的最短路径，用SPFA即可。

import java.util.*;
import java.io.*;
import java.util.List;

public class Main {
    static BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));
    static BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));
    public static void main(String[] args) throws IOException {
        String[] input = reader.readLine().trim().split(" ");
        int t = Integer.parseInt(input[0]);
        int r = Integer.parseInt(input[1]);
        int p = Integer.parseInt(input[2]);
        int s = Integer.parseInt(input[3]);
//        道路是双向的，可以从 Ai 到 Bi，也可以从 Bi 到 Ai，花费都是 Ci
//        然而航线与之不同，只可以从 Ai 到 Bi

//        出台了一些政策：保证如果有一条航线可以从 Ai 到 Bi
//        那么保证不可能通过一些道路和航线从 Bi 回到 Ai。
        // 建图
        List<int[]>[] graph = new LinkedList[t + 1];
        for (int i = 0; i < t + 1; i++) graph[i] = new LinkedList<>();
        while (r-- > 0) {
            // 道路，双向，非负
            input = reader.readLine().trim().split(" ");
            int a = Integer.parseInt(input[0]);
            int b = Integer.parseInt(input[1]);
            int c = Integer.parseInt(input[2]);
            graph[a].add(new int[] {b, c});
            graph[b].add(new int[] {a, c});
        }
        while (p-- > 0) {
            // 航道，单向，可能为负
            input = reader.readLine().trim().split(" ");
            int a = Integer.parseInt(input[0]);
            int b = Integer.parseInt(input[1]);
            int c = Integer.parseInt(input[2]);
            graph[a].add(new int[] {b, c});
        }
        // 带负权值的最短路径，用spfa
        Deque<Integer> queue = new LinkedList<>();
        queue.offer(s);
        boolean[] vis = new boolean[t + 1];
        vis[s] = true;
        int[] dist = new int[t + 1];
        Arrays.fill(dist, 0x3f3f3f3f);
        dist[s] = 0;
        while (!queue.isEmpty()) {
            int u = queue.poll();
            vis[u] = false;
            for (int[] next : graph[u]) {
                int v = next[0];
                int w = next[1];
                if (dist[v] > dist[u] + w) {
                    dist[v] = dist[u] + w;
                    if (vis[v] == false) {
                        vis[v] = true;
                        queue.offer(v);
                    }
                }
            }
        }
        for (int i = 1; i <= t; i++) {
            if (dist[i] == 0x3f3f3f3f) {
                writer.write("NO PATH" + "\n");
            } else {
                writer.write(dist[i] + "\n");
            }
        }
        writer.flush();
    }
}

图论算法的学习到这里就差不多结束了！一定要记得多刷题，多背模板！