【算法修炼】回溯专题二——岛屿类问题和迷宫类问题

原创已于 2022-02-11 21:43:01 修改 · 739 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #深度优先 #java

于 2022-02-07 20:26:34 首次发布

算法修炼专栏收录该内容

47 篇文章

订阅专栏

本文详细介绍了使用深度优先搜索（DFS）和广度优先搜索（BFS）解决岛屿计数、封闭岛屿、最大岛屿面积、子岛屿统计、不同岛屿数量以及迷宫类问题的方法。通过DFS和BFS的框架及方向数组，展示了如何遍历二维矩阵并处理各种题目要求。同时，讨论了DFS和BFS在选择上的考虑，如BFS适用于寻找最短路径，而DFS则适合搜索所有解。

专题二主要对岛屿类型问题、迷宫类型问题进行讲解，它们有固定的套路，是可以一起学习的。这类题目可以使用dfs、bfs解决，但它们的本质都是通过遍历、标记、剪枝来解决，有些题目使用dfs可能会超时，必须得使用bfs

回溯专题二

// 二维矩阵遍历框架
void dfs(int[][] grid, int i, int j, boolean[] visited) {
    int m = grid.length, n = grid[0].length;
    if (i < 0 || j < 0 || i >= m || j >= n) {
        // 超出索引边界
        return;
    }
    if (visited[i][j]) {
        // 已遍历过 (i, j)
        return;
    }
    // 进入节点 (i, j)
    visited[i][j] = true;
    dfs(grid, i - 1, j, visited); // 上
    dfs(grid, i + 1, j, visited); // 下
    dfs(grid, i, j - 1, visited); // 左
    dfs(grid, i, j + 1, visited); // 右
}

这类题目一般都需要上下左右移动，可以使用上面的方式，也可以通过使用方向数组实现。

// 方向数组，分别代表上、下、左、右
int[][] dirs = new int[][]{{-1,0}, {1,0}, {0,-1}, {0,1}};

void dfs(int[][] grid, int i, int j, boolean[] visited) {
    int m = grid.length, n = grid[0].length;
    if (i < 0 || j < 0 || i >= m || j >= n) {
        // 超出索引边界
        return;
    }
    if (visited[i][j]) {
        // 已遍历过 (i, j)
        return;
    }

    // 进入节点 (i, j)
    visited[i][j] = true;
    // 递归遍历上下左右的节点
    for (int[] d : dirs) {
        int next_i = i + d[0];
        int next_j = j + d[1];
        dfs(grid, next_i, next_j, visited);
    }
    // 离开节点 (i, j)
}

一、岛屿类题目

1.1 岛屿数量（中等）

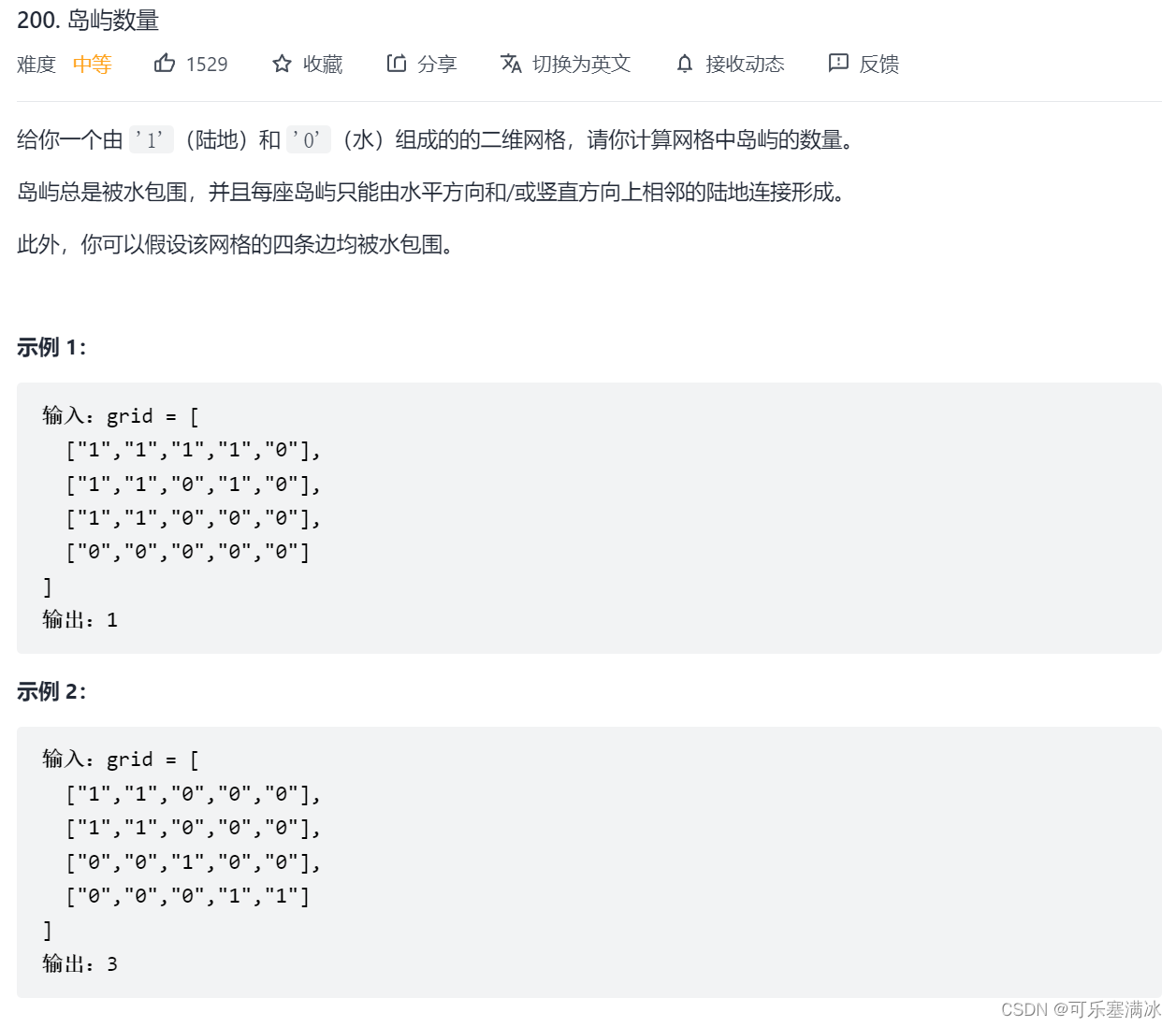
在这里插入图片描述
统计岛屿的数量，岛屿必须得为1，并且两个岛屿之间必须要用0间隔开，这样的两个岛屿才算独立。考虑到有vis数组记录是否访问，我们可以从有1的地方开始遍历，把与它相连的所有1都标记，直到它的所有方位都无法遍历才返回（dfs），再访问下一个有1的地方时，我们可以判断它是否被访问过，如果被访问过说明它和第一个岛屿是相连的，不能算作单独新的岛屿；如果没有访问过，此时就出现了新的岛屿。

class Solution {
    // 记录是否访问
    int[][] vis = new int[301][301];
    public int numIslands(char[][] grid) {
        int len1 = grid.length;
        int len2 = grid[0].length;
        int ans = 0;
        for (int i = 0; i < len1; i++) {
            for (int j = 0; j < len2; j++) {
            	// 一定要为 1，并且不能被访问过才能继续遍历
                if (grid[i][j] == '1' && vis[i][j] == 0) {
                    ans++;
                    dfs(grid, i, j);
                }
            }
        }
        return ans;
    }
    void dfs(char[][] grid, int i, int j) {
        int len1 = grid.length;
        int len2 = grid[0].length;
        // 超出边界、已经visited、遍历到海水
        if (i < 0 || j < 0 || i >= len1 || j >= len2 || vis[i][j] == 1 || grid[i][j] == '0') return;
        // 当前位置标记为已访问
        vis[i][j] = 1;
        // 依次遍历，上下右左
        dfs(grid, i + 1, j);
        dfs(grid, i - 1, j);
        dfs(grid, i, j + 1);
        dfs(grid, i, j - 1);
    }
}

也可以不用vis数组，只要与当前岛屿相连的1，我们都置为0，把它们都淹没掉，代码如下：

class Solution {
    public int numIslands(char[][] grid) {
        int len1 = grid.length;
        int len2 = grid[0].length;
        int ans = 0;
        for (int i = 0; i < len1; i++) {
            for (int j = 0; j < len2; j++) {
                if (grid[i][j] == '1') {
                    ans++;
                    dfs(grid, i, j);
                }
            }
        }
        return ans;
    }
    void dfs(char[][] grid, int i, int j) {
        int len1 = grid.length;
        int len2 = grid[0].length;
        if (i < 0 || j < 0 || i >= len1 || j >= len2 || grid[i][j] == '0') return;
        // 与岛屿相连的1置为0，把它们淹没
        grid[i][j] = '0';
        // 依次遍历，上下右左
        dfs(grid, i + 1, j);
        dfs(grid, i - 1, j);
        dfs(grid, i, j + 1);
        dfs(grid, i, j - 1);
    }
}

上面的代码执行时间就远远快于需要vis数组的代码。

当然也可以使用方向数组实现，在dfs函数里面需要多写一个for循环用来遍历方向数组。（可以自己尝试尝试）

1.2 统计封闭岛屿的数目（中等）

在这里插入图片描述
注意本题中的陆地是0，水是1，要是封闭岛屿，它就不能有陆地在四条边的位置，我们可以先遍历四条边，把有岛屿以及与之相连的位置全部标记，标记完后再全部遍历，这样就可以求出答案。（也可以选择使用vis数组进行标记）

class Solution {
    public int closedIsland(int[][] grid) {
        // 注意本题：陆地是0，水是1
        int m = grid.length;
        int n = grid[0].length;
        int ans = 0;
        // 遍历第一列靠边的岛屿
        for (int i = 0; i < m; i++) {
            if (grid[i][0] == 0) {
                dfs(grid, i, 0);
            }
        }
        // 遍历最后一列靠边的岛屿
        for (int i = 0; i < m; i++) {
            if (grid[i][n - 1] == 0) {
                dfs(grid, i, n - 1);
            }
        }
        // 遍历第一行靠边的岛屿
        for (int i = 0; i < n; i++) {
            if (grid[0][i] == 0) {
                dfs(grid, 0, i);
            }
        }
        // 遍历最后一行靠边的岛屿
        for (int i = 0; i < n; i++) {
            if (grid[m - 1][i] == 0) {
                dfs(grid, m - 1, i);
            }
        }
        // 上面的四个循环可以把靠边的岛屿全部淹没，剩下的就是封闭的岛屿
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 0) {
                    ans++;
                    dfs(grid, i, j);
                }
            }
        }
        return ans;
    }
    void dfs(int[][] grid, int i, int j) {
        int m = grid.length;
        int n = grid[0].length;
        // 超出边界或者
        if (i < 0 || j < 0 || i >= m || j >= n || grid[i][j] == 1) {
            return;
        }
        // 把遍历到的陆地淹没（替换vis数组的作用）
        grid[i][j] = 1;
        dfs(grid, i + 1, j);
        dfs(grid, i - 1, j);
        dfs(grid, i, j + 1);
        dfs(grid, i, j - 1);
    }
}

1.3 岛屿的最大面积（中等）

在这里插入图片描述
和之前题目类似，但是要统计每个岛屿的面积，这就需要改变dfs函数的返回类型，我们需要统计1的个数，每当当前的位置是1（岛屿），dfs它四个方向 + 1就是当前岛屿的面积，如果走到边界区或者为0，就返回0，即当前位置不计入岛屿面积。

class Solution {
    public int maxAreaOfIsland(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int ans = 0;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 1) {
                    // 统计最大面积
                    ans = Math.max(ans, dfs(grid, i, j));
                }
            }
        }
        return ans;
    }
    int dfs(int[][] grid, int i, int j) {
        int m = grid.length;
        int n = grid[0].length;
        if (i < 0 || j < 0 || i >= m || j >= n || grid[i][j] == 0) {
            return 0;
        }
        // 访问过的陆地被淹没
        grid[i][j] = 0;
        // 统计周围的所有陆地
        return dfs(grid, i + 1, j) +
		        dfs(grid, i - 1, j) +
		        dfs(grid, i, j + 1) +
		        dfs(grid, i, j - 1) + 1;
    }
}

一定要注意面积是如何统计的。

1.4 统计子岛屿（中等）

在这里插入图片描述
难点在于如何确定子岛屿，根据题目意思，我们知道如果在grid1中的某位置为0（水），而grid2中对应的位置为1（陆地），那么grid2中与该陆地相连的岛屿就不是子岛屿。可以先遍历grid1[i][j]中为0，grid2[i][j]中为1的陆地，把这些陆地都淹没（因为它们不是子岛屿），然后再遍历grid2中剩下的岛屿，就是grid1的子岛屿。

class Solution {
    public int countSubIslands(int[][] grid1, int[][] grid2) {
        // 我们可以把grid1中为0，但grid2中为1的岛屿（相连的1）全都淹没掉
        // 因为grid2的这些岛屿不可能是grid1的子岛屿
        int m = grid2.length;
        int n = grid2[0].length;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid1[i][j] == 0 && grid2[i][j] == 1) {
                    dfs(grid2, i, j);
                }
            }
        }
        // 把grid2中不满足子岛屿的岛屿全都淹没，剩下的岛屿就是grid1的子岛屿
        int ans = 0;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid2[i][j] == 1) {
                    ans++;
                    dfs(grid2, i, j);
                }
            }
        }
        return ans;
    }
    void dfs(int[][] grid, int i, int j) {
        int m = grid.length;
        int n = grid[0].length;
        if (i < 0 || j < 0 || i >= m || j >= n || grid[i][j] == 0) {
            return;
        }
        grid[i][j] = 0;
        dfs(grid, i + 1, j);
        dfs(grid, i - 1, j);
        dfs(grid, i, j + 1);
        dfs(grid, i, j - 1);
    }
}

1.5 ※不同的岛屿数量（中等）

在这里插入图片描述
如何保留岛屿的形状？ 这是很难的一点。注意到，如果连个岛屿的形状相同，那么遍历这个岛屿的序列应该也是相同的。

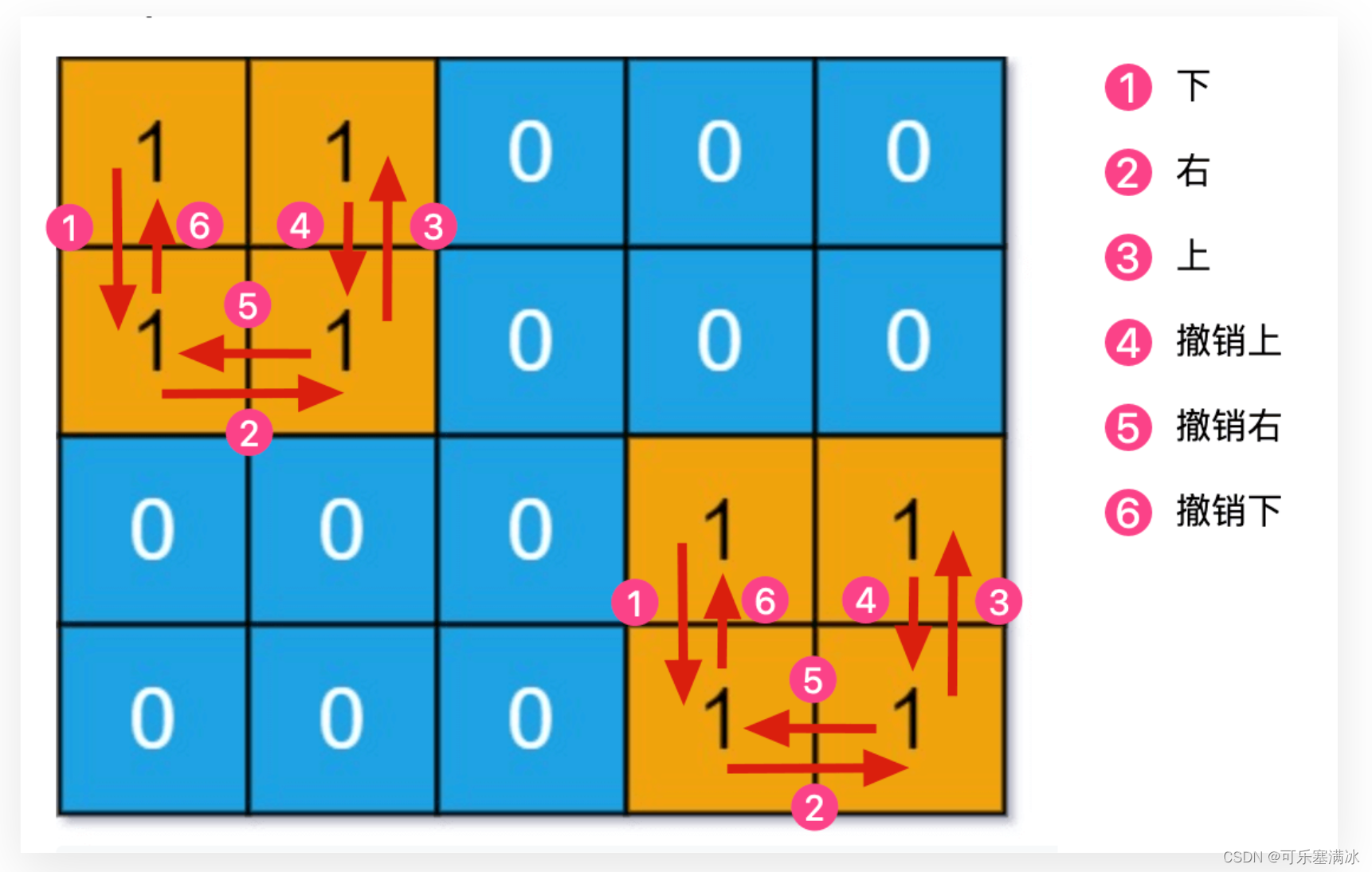
假设它们的遍历顺序是：
下，右，上，撤销上，撤销右，撤销下

如果我用分别用 1, 2, 3, 4 代表上下左右，用 -1, -2, -3, -4 代表上下左右的撤销，那么可以这样表示它们的遍历顺序：
2, 4, 1, -1, -4, -2

这就相当于是岛屿序列化的结果，只要每次使用 dfs 遍历岛屿的时候生成这串数字进行比较，就可以计算到底有多少个不同的岛屿了。用set记录每个岛屿的遍历序列，然后返回set的size即可。

class Solution {
    public int numDistinctIslands(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        HashSet<String> set = new HashSet<>();
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 1) {
                    StringBuilder str = new StringBuilder();
                    // 初始的开始位置dir任意设置
                    dfs(grid, i, j, str, 99);
                    System.out.println(str);
                    set.add(str.toString());
                }
            }
        }
        return set.size();
    }
    void dfs(int[][] grid, int i, int j, StringBuilder str, int dir) {
        int m = grid.length;
        int n = grid[0].length;
        if (i < 0 || j < 0 || i >= m || j >= n || grid[i][j] == 0) {
            return;
        }
        // 访问过的陆地被淹没
        grid[i][j] = 0;
        // 前序遍历位置：进入(i,j)
        str.append(dir).append(',');
        // dfs四个方向
        // 上下左右依次对应：1234
        // 往回遍历的上下左右对应：-1 -2 -3 -4
        dfs(grid, i - 1, j, str, 1);
        dfs(grid, i + 1, j, str, 2);
        dfs(grid, i, j - 1, str, 3);
        dfs(grid, i, j + 1, str, 4);
        // 后续遍历
        str.append(-dir).append(',');
    }
}

1.6 颜色填充（简单）

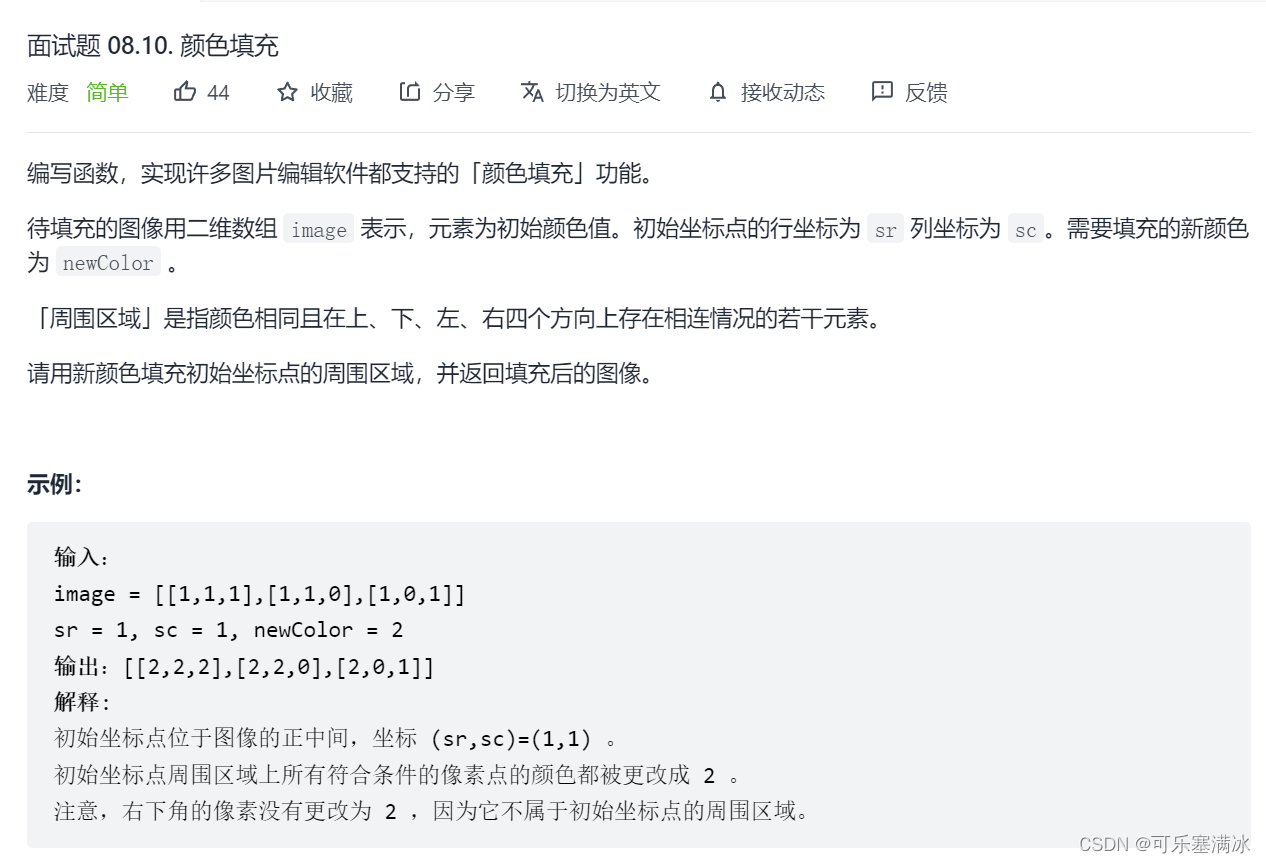
在这里插入图片描述
记录一下oldColor，只把相连的且color与开始位置相同的oldcolor颜色相同的位置填充为newColor，注意有可能oldColor = newColor，此时就不用填充，直接返回原image数组。

class Solution {
    public int[][] floodFill(int[][] image, int sr, int sc, int newColor) {
        int oldColor = image[sr][sc];
        if (oldColor != newColor) {
            dfs(image, sr, sc, newColor, oldColor);
        }
        return image;
    }
    void dfs(int[][] image, int sr, int sc, int newColor, int oldColor) {
        int m = image.length;
        int n = image[0].length;
        if (sr < 0 || sc < 0 || sr >= m || sc >= n || image[sr][sc] == newColor || image[sr][sc] != oldColor) {
            return;
        }
        image[sr][sc] = newColor;
        dfs(image, sr - 1, sc, newColor, oldColor);
        dfs(image, sr + 1, sc, newColor, oldColor);
        dfs(image, sr, sc - 1, newColor, oldColor);
        dfs(image, sr, sc + 1, newColor, oldColor);
    }
}

二、迷宫类题目

迷宫类题目，一般都会给出开始起点，和终点，更适合使用方向数组进行求解，并且一定要注意迷宫类题目需要回溯！！！

2.1 迷宫一（简单）

在这里插入图片描述

需要注意java读入字符串数组的方式，在读入的同时记录下S的位置坐标，因为只需要知道能否到达迷宫出口，所以我们可以让dfs函数输出boolean，当到达该出口时return true，其余情况就return false，然后求四个方向结果的“或”，因为只要能到达迷宫出口即可。

import java.util.Scanner;

public class Main {
    static boolean flag = false;
    static int[][] vis = new int[11][11];
    static int[] x = new int[] {-1, 1, 0, 0};
    static int[] y = new int[] {0, 0, -1, 1};
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        int m = scan.nextInt();
        char[][] map = new char[n][m];
        int bi = 0;
        int bj = 0;
        for (int i = 0; i < n; i++) {
            map[i] = scan.next().toCharArray();
            for (int j = 0; j < m; j++) {
                if (map[i][j] == 'S') {
                    bi = i;
                    bj = j;
                }
            }
        }
        vis[bi][bj] = 1;
        dfs(map, bi, bj);
        if (flag) {
            System.out.println("yes");
        } else {
            System.out.println("no");
        }
    }
    static void dfs(char[][] map, int bi, int bj) {
        int n = map.length;
        int m = map[0].length;
        if (map[bi][bj] == 'T') {
            flag = true;
            return;
        }
        for (int i = 0; i < 4; i++) {
            int tmpx = bi + x[i];
            int tmpy = bj + y[i];
            if (tmpx < 0 || tmpy < 0 || tmpx >= n || tmpy >= m || vis[tmpx][tmpy] == 1 || map[tmpx][tmpy] == '*') {
                continue;
            }
            // 如果能够到达终点那就不用再找了
            if (flag) {
            	continue;
            }
            vis[tmpx][tmpy] = 1;
            dfs(map, tmpx, tmpy);
            // 一定要记得回溯
            vis[tmpx][tmpy] = 0;
        }
    }
}

2.2 迷宫二（中等）

在这里插入图片描述

关键在于如何求解和更新最小步数，可以在dfs函数的参数里面加上cnt参数，只有到达终点时才记录cnt。

import java.util.Scanner;

public class Main {
    static int[][] vis = new int[11][11];
    static int[] x = new int[] {-1, 1, 0, 0};
    static int[] y = new int[] {0, 0, -1, 1};
    static int ans = 999;
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        int m = scan.nextInt();
        char[][] map = new char[n][m];
        int bi = 0;
        int bj = 0;
        for (int i = 0; i < n; i++) {
            map[i] = scan.next().toCharArray();
            for (int j = 0; j < m; j++) {
                if (map[i][j] == 'S') {
                    bi = i;
                    bj = j;
                }
            }
        }
        // 起点一定要记得标记
        vis[bi][bj] = 1;
        dfs(map, bi, bj, 0);
        if (ans == 999) {
            System.out.println(-1);
        } else {
            System.out.println(ans);
        }
    }
    static void dfs(char[][] map, int bi, int bj, int cnt) {
        int n = map.length;
        int m = map[0].length;
        // 如果cnt大于ans那就别找了
        if (cnt >= ans) {
            return;
        }
        if (map[bi][bj] == 'T') {
            ans = cnt;
            return;
        }
        for (int i = 0; i < 4; i++) {
            int tmpx = bi + x[i];
            int tmpy = bj + y[i];
            if (tmpx < 0 || tmpy < 0 || tmpx >= n || tmpy >= m || vis[tmpx][tmpy] == 1 || map[tmpx][tmpy] == '*') {
                continue;
            }
            vis[tmpx][tmpy] = 1;
            dfs(map, tmpx, tmpy, cnt + 1);
            vis[tmpx][tmpy] = 0;
        }
    }
}

2.3 迷宫三（中等）

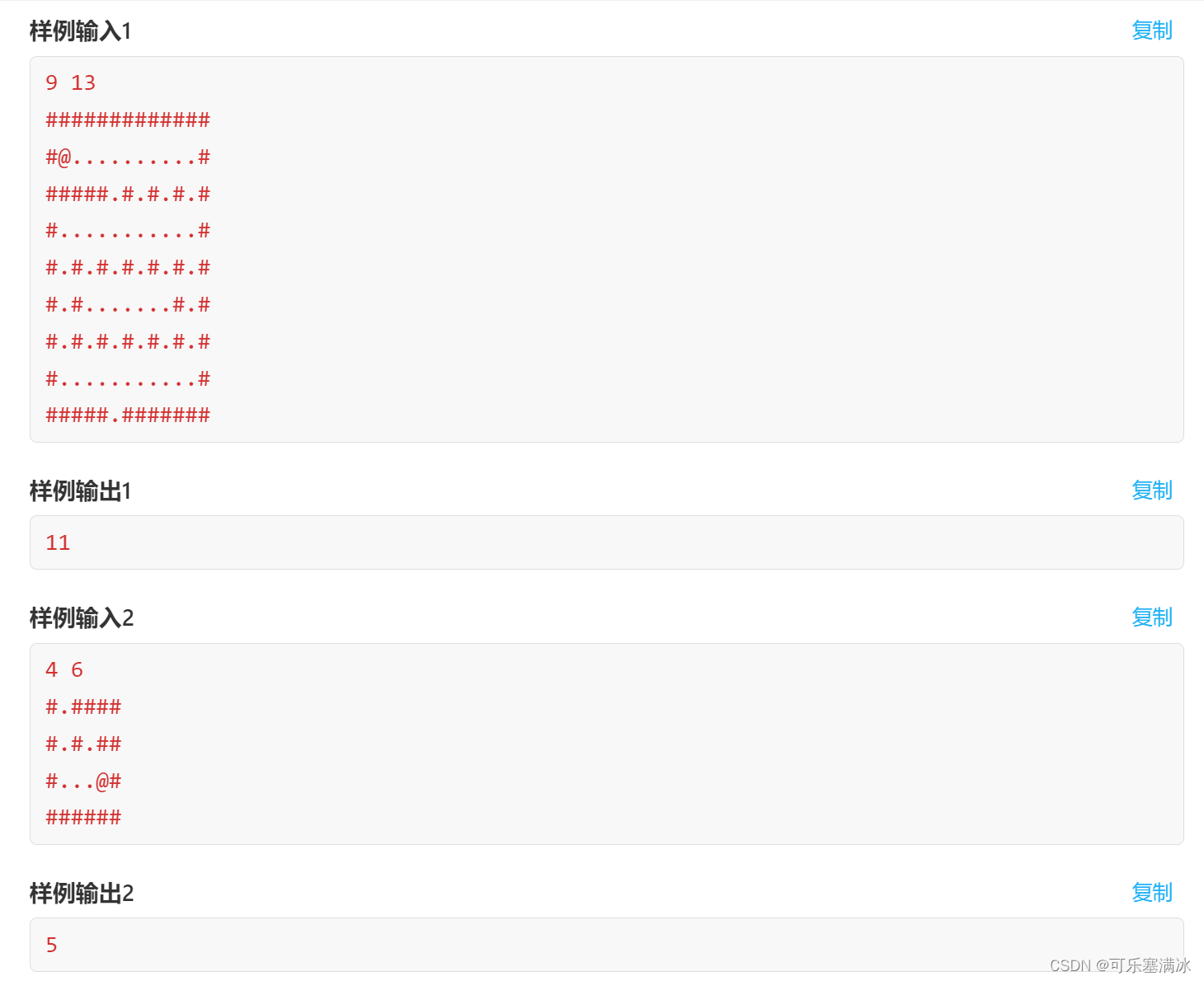
在这里插入图片描述

相比于上一题，没有具体的终点，只要在边上且为点，就可以视为终点，基于此，只需要修改判别终点的代码即可。

import java.util.Scanner;

public class Main {
    static int[][] vis = new int[20][20];
    static int[] x = new int[] {-1, 1, 0, 0};
    static int[] y = new int[] {0, 0, -1, 1};
    static int ans = 999;
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        int m = scan.nextInt();
        char[][] map = new char[n][m];
        int bi = 0;
        int bj = 0;
        for (int i = 0; i < n; i++) {
            map[i] = scan.next().toCharArray();
            for (int j = 0; j < m; j++) {
                if (map[i][j] == '@') {
                    bi = i;
                    bj = j;
                }
            }
        }
        // 起点一定要记得标记
        vis[bi][bj] = 1;
        dfs(map, bi, bj, 0);
        if (ans == 999) {
            System.out.println(-1);
        } else {
            System.out.println(ans);
        }
    }
    static void dfs(char[][] map, int bi, int bj, int cnt) {
        int n = map.length;
        int m = map[0].length;
        // 如果cnt大于ans那就别找了
        if (cnt >= ans) {
            return;
        }
        // 主要是修改终点的判别方式
        if (map[bi][bj] == '.' && (bi == 0 || bi == n - 1 || bj == 0 || bj == m -1)) {
            ans = cnt;
            return;
        }
        for (int i = 0; i < 4; i++) {
            int tmpx = bi + x[i];
            int tmpy = bj + y[i];
            if (tmpx < 0 || tmpy < 0 || tmpx >= n || tmpy >= m || vis[tmpx][tmpy] == 1 || map[tmpx][tmpy] == '#') {
                continue;
            }
            vis[tmpx][tmpy] = 1;
            dfs(map, tmpx, tmpy, cnt + 1);
            vis[tmpx][tmpy] = 0;
        }
    }
}

2.4 红与黑（中等）

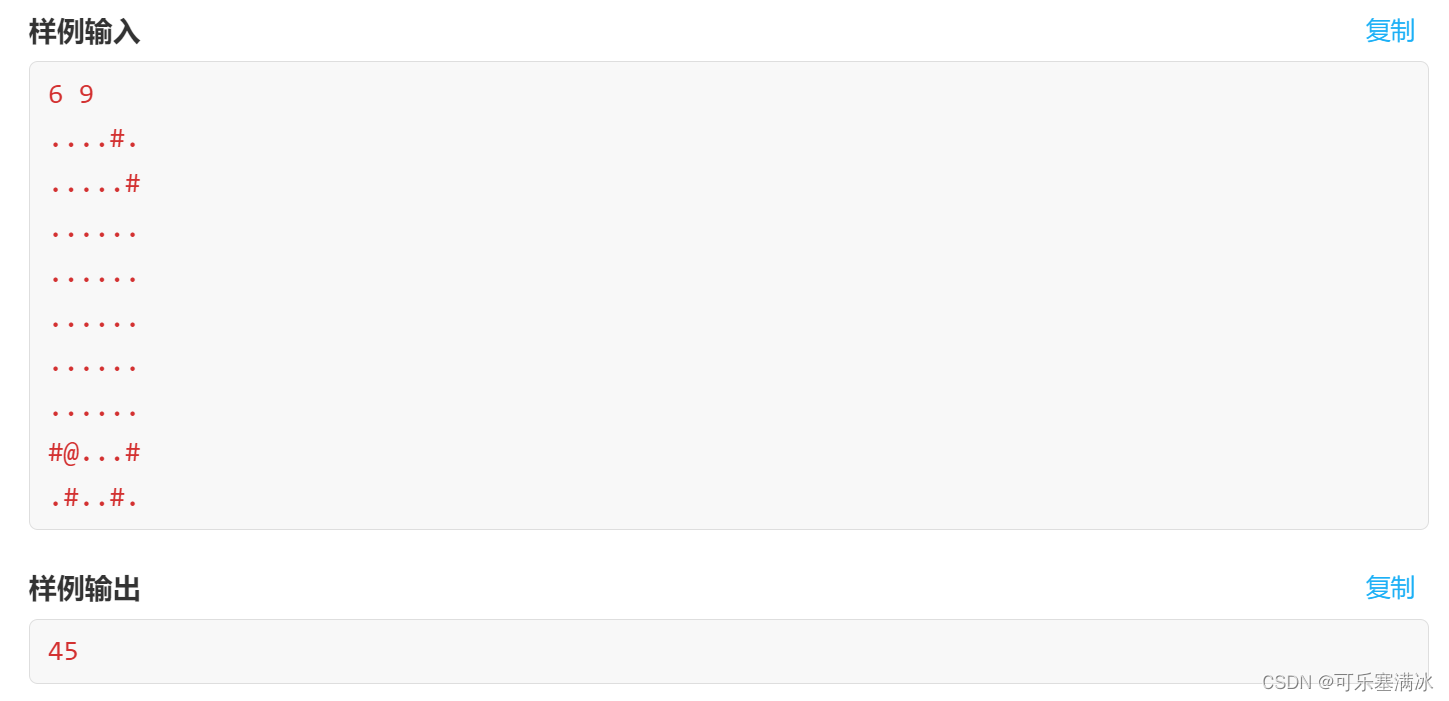
在这里插入图片描述

这道题需要统计能到达的所有黑色方块个数，不是找路径、路线，所以不需要回溯，和之前岛屿类问题一样，一旦能够访问就计数++。

import java.util.Scanner;

public class Main {
    static int[][] vis = new int[30][30];
    static int[] x = new int[] {-1, 1, 0, 0};
    static int[] y = new int[] {0, 0, -1, 1};
    static int ans = 1;
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        int m = scan.nextInt();
        char[][] map = new char[m][n];
        int bi = 0;
        int bj = 0;
        for (int i = 0; i < m; i++) {
            map[i] = scan.next().toCharArray();
            for (int j = 0; j < n; j++) {
                if (map[i][j] == '@') {
                    bi = i;
                    bj = j;
                }
            }
        }
        // 起点一定要记得标记
        vis[bi][bj] = 1;
        dfs(map, bi, bj);
        System.out.println(ans);
    }
    static void dfs(char[][] map, int bi, int bj) {
        int m = map.length;
        int n = map[0].length;
        for (int i = 0; i < 4; i++) {
            int tmpx = bi + x[i];
            int tmpy = bj + y[i];
            if (tmpx < 0 || tmpy < 0 || tmpx >= m || tmpy >= n || vis[tmpx][tmpy] == 1 || map[tmpx][tmpy] == '#') {
                continue;
            }
            ans++;
            vis[tmpx][tmpy] = 1;
            dfs(map, tmpx, tmpy);
        }
    }
}

2.5 仙岛求药（中等）

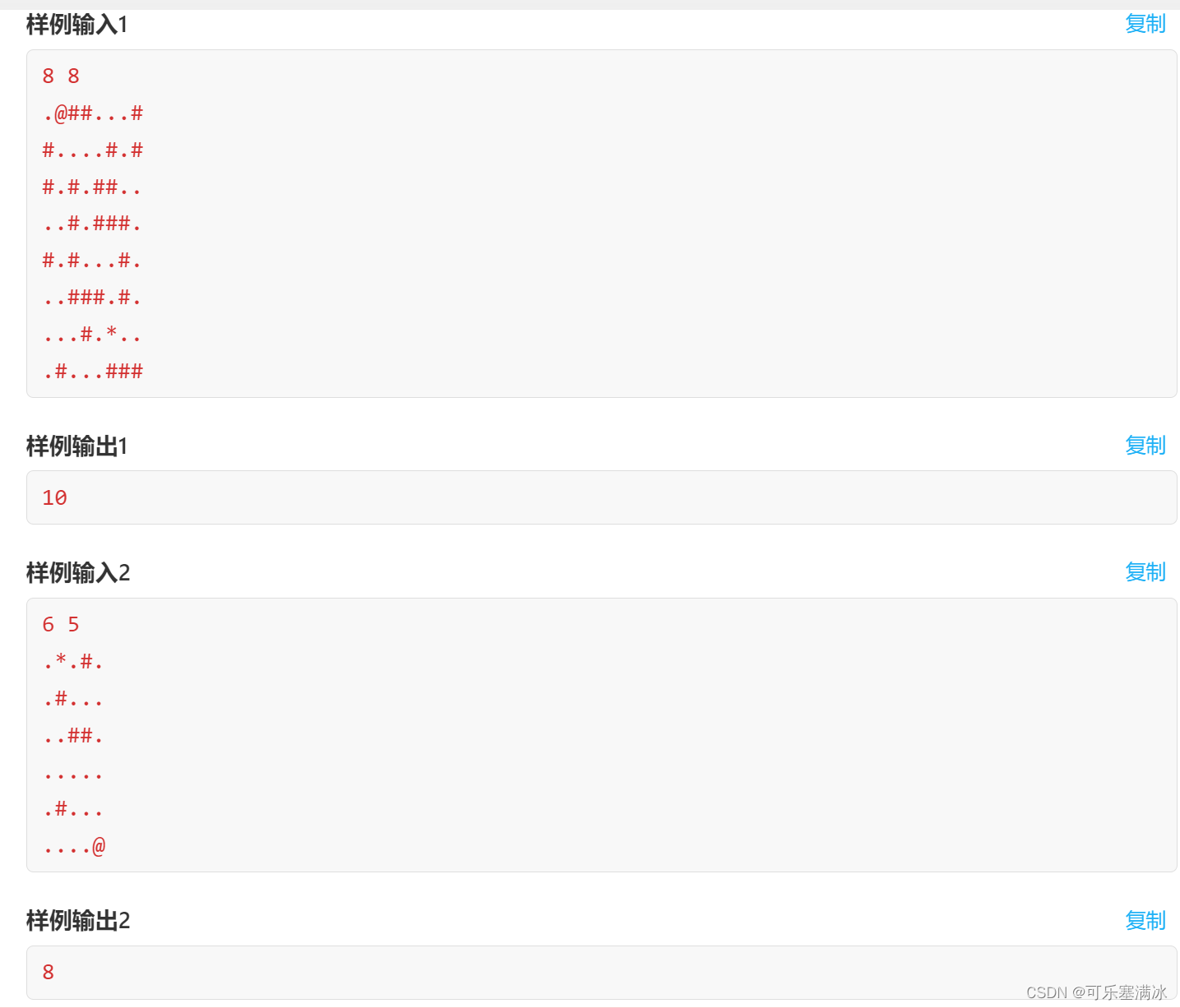
在这里插入图片描述

先给出dfs解法：

import java.util.Scanner;

public class Main {
    static int[][] vis = new int[30][30];
    static int[] x = new int[] {-1, 1, 0, 0};
    static int[] y = new int[] {0, 0, -1, 1};
    static int ans = 99;
    static int bi, bj;
    static int m, n;
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        m = scan.nextInt();
        n = scan.nextInt();
        char[][] map = new char[m][n];
        for (int i = 0; i < m; i++) {
            map[i] = scan.next().toCharArray();
            for (int j = 0; j < n; j++) {
                if (map[i][j] == '@') {
                    bi = i;
                    bj = j;
                }
            }
        }
        vis[bi][bj] = 1;
        dfs(map, bi, bj, 0);
        if (ans == 99) {
            System.out.println(-1);
        } else {
            System.out.println(ans);
        }
    }
    static void dfs(char[][] map, int i, int j, int cnt) {
        if (cnt >= ans) {
            return;
        }
        if (map[i][j] == '*') {
            // 更新最小值
            ans = Math.min(cnt, ans);
            return;
        }
        for (int k = 0; k < 4; k++) {
            int tmpx = i + x[k];
            int tmpy = j + y[k];
            if (tmpx < 0 || tmpy < 0 || tmpx >= m || tmpy >= n || vis[tmpx][tmpy] == 1 || map[tmpx][tmpy] == '#') {
                continue;
            }
            vis[tmpx][tmpy] = 1;
            dfs(map, tmpx, tmpy, cnt + 1);
            vis[tmpx][tmpy] = 0;
        }
    }
}

最后一个样例无法通过，超时了，因为dfs会进行很多重复的搜索，这里必须要使用bfs才能完成，bfs也是有模板的，如下。

import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
// Queue存储的结点
class node {
    int x, y, step;
    // 下面生成函数一定要写！！！
    node() {}
    node(int x, int y, int step) {
        this.x = x;
        this.y = y;
        this.step = step;
    }
}
public class Main {
    public static void main(String[] args) {
        // 用LinkedList来生成Queue
        Queue<node> Q = new LinkedList<>();
        for (int i = 0; i < m; i++) {
            map[i] = scan.next().toCharArray();
            for (int j = 0; j < n; j++) {
                if (map[i][j] == '@') {
                    // 计数包括初始位置的方块
                    node b = new node(i, j, 1);
                    vis[i][j] = 1;
                    // 入队
                    Q.offer(b);
                }
            }
        }
        // 开始BFS
        while(!Q.isEmpty()) {
            // 直接弹出队列
            // peek是查看头，poll是取出头
            node tmp = Q.poll();
            // 找到终点
            if (map[tmp.x][tmp.y] == '*') {
                // 计数不包括最后的终点
                ans = Math.min(ans, tmp.step - 1);
            }
            for (int i = 0; i < 4; i++) {
            	// 看下一个结点是否满足要求，满足才入队
                node temp = new node();
                temp.x = tmp.x + x[i];
                temp.y = tmp.y + y[i];
                // 不满足条件就continue
                if (temp.x < 0 || temp.y < 0 || temp.x >= m || temp.y >= n || vis[temp.x][temp.y] == 1 || map[temp.x][temp.y] == '#') {
                    continue;
                }
                vis[temp.x][temp.y] = 1;
                // 满足条件step + 1
                temp.step = tmp.step + 1;
                // 入队
                Q.offer(temp);
                // 注意BFS不需要回溯！
            }
        }
    }
}

注意java中的队列的相应函数：
在这里插入图片描述
一般我们使用队列Queue，用LinkedList作为实现类。
使用bfs本题就可以很快得到结果。

import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
// Queue存储的结点
class node {
    int x, y, step;
    node() {}
    node(int x, int y, int step) {
        this.x = x;
        this.y = y;
        this.step = step;
    }
}
public class Main {
    public static void main(String[] args) {
        int[][] vis = new int[30][30];
        int[] x = new int[] {-1, 1, 0, 0};
        int[] y = new int[] {0, 0, -1, 1};
        int ans = 99;
        int m, n;
        Scanner scan = new Scanner(System.in);
        m = scan.nextInt();
        n = scan.nextInt();
        char[][] map = new char[m][n];
        // 用LinkedList来生成Queue
        Queue<node> Q = new LinkedList<>();
        for (int i = 0; i < m; i++) {
            map[i] = scan.next().toCharArray();
            for (int j = 0; j < n; j++) {
                if (map[i][j] == '@') {
                    // 计数包括初始位置的方块
                    node b = new node(i, j, 1);
                    vis[i][j] = 1;
                    // 入队
                    Q.offer(b);
                }
            }
        }
        // 开始BFS
        while(!Q.isEmpty()) {
            node tmp = Q.poll();
            if (map[tmp.x][tmp.y] == '*') {
                // 计数不包括最后的终点
                ans = Math.min(ans, tmp.step - 1);
            }
            for (int i = 0; i < 4; i++) {
                node temp = new node();
                temp.x = tmp.x + x[i];
                temp.y = tmp.y + y[i];
                // 不满足条件就continue
                if (temp.x < 0 || temp.y < 0 || temp.x >= m || temp.y >= n || vis[temp.x][temp.y] == 1 || map[temp.x][temp.y] == '#') {
                    continue;
                }
                vis[temp.x][temp.y] = 1;
                // 满足条件step + 1
                temp.step = tmp.step + 1;
                Q.offer(temp);
                // 注意BFS不需要回溯！
            }
        }
        if (ans == 99) {
            System.out.println(-1);
        } else {
            System.out.println(ans);
        }
    }
}

求最短路径、最少步数，最好的方式是用bfs，dfs也可以但是会多花一些时间。

2.6 马走日（困难）

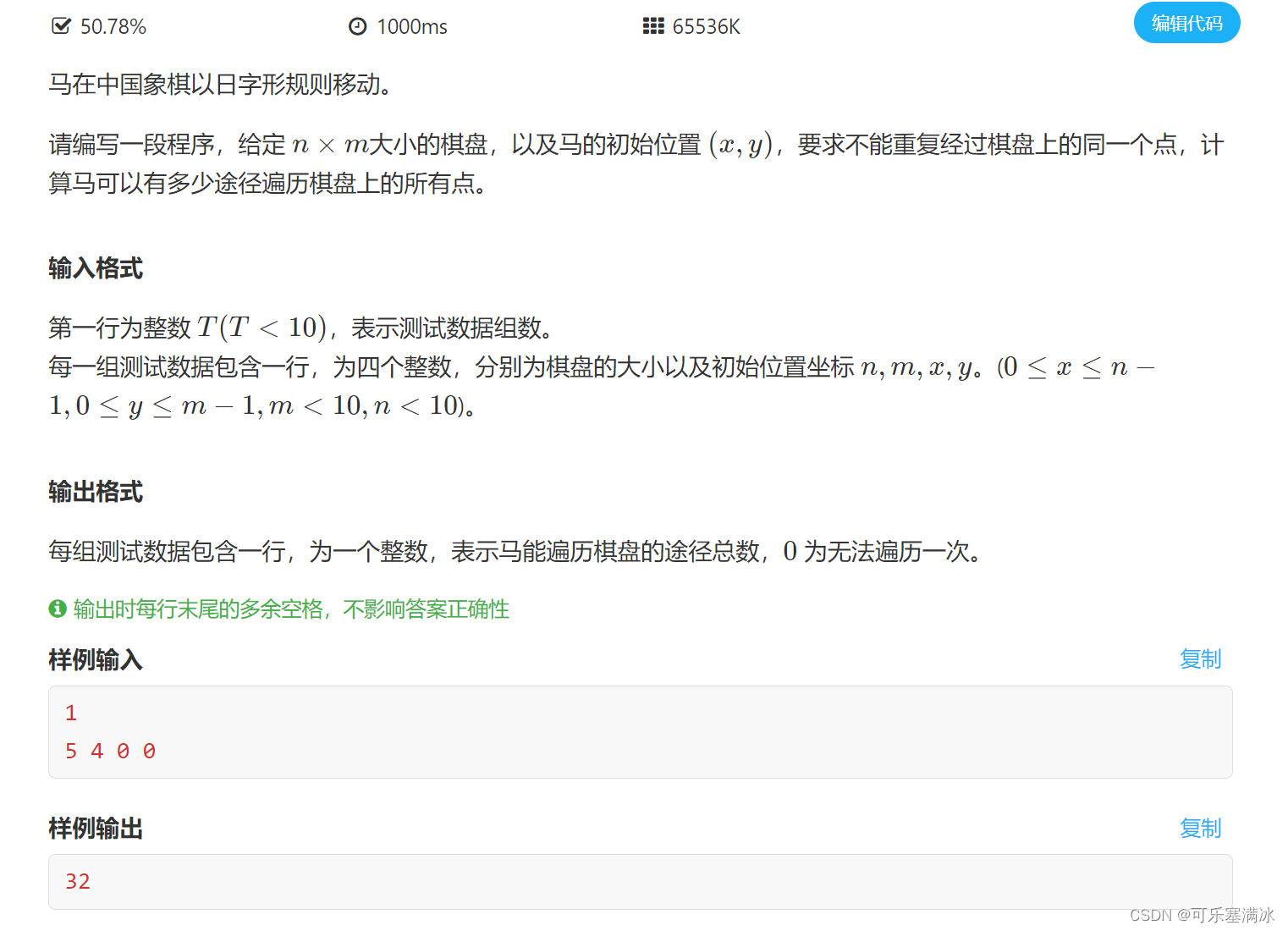
在这里插入图片描述
难点在于马的行进方向，应该是有8个方向，用草稿纸画一画，用方向矩阵来模拟。还要注意static变量，再每次循环时要把它们置零！

import java.util.Scanner;
public class Main {
    static int[] xx = {1, 2, 2, 1, -1, -2, -2, -1};
    static int[] yy = {2, 1, -1, -2, -2, -1, 1, 2};
    static int[][] vis = new int[30][30];
    static int n, m;
    static int ans = 0;
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int T = scan.nextInt();
        while (T > 0) {
            // 注意static变量在每次循环时要置0
            ans = 0;
            vis = new int[30][30];
            n = scan.nextInt();
            m = scan.nextInt();
            int x = scan.nextInt();
            int y = scan.nextInt();
            vis[x][y] = 1;
            dfs(x, y, 1);
            System.out.println(ans);
            T--;
        }
    }
    static void dfs(int x, int y, int cnt) {
        // 能够遍历完所有棋盘点，那就看计数==n * m
        if (cnt == n * m) {
            ans++;
            return;
        }
        for (int i = 0; i < 8; i++) {
            int tempx = x + xx[i];
            int tempy = y + yy[i];
            if (tempx < 0 || tempy < 0 || tempx >= n || tempy >= m || vis[tempx][tempy] == 1) {
                continue;
            }
            vis[tempx][tempy] = 1;
            dfs(tempx, tempy, cnt + 1);
            // 记得回溯！
            vis[tempx][tempy] = 0;
        }
    }
}

三、DFS和BFS的选择

1.BFS是用来搜索最短径路的解是比较合适的，比如求最少步数的解，最少交换次数的解，因为BFS搜索过程中遇到的解一定是离根最近的，所以遇到一个解，一定就是最优解，此时搜索算法可以终止。这个时候不适宜使用DFS，因为DFS搜索到的解不一定是离根最近的，只有全局搜索完毕，才能从所有解中找出离根的最近的解。（当然这个DFS的不足，可以使用迭代加深搜索ID-DFS去弥补）

2.空间优劣上，DFS是有优势的，DFS不需要保存搜索过程中的状态，而BFS在搜索过程中需要保存搜索过的状态，而且一般情况需要一个队列来记录。

3.DFS适合搜索全部的解，而正因为要搜索全部的解，那么BFS搜索过程中，遇到离根最近的解，并没有什么用，也必须遍历完整棵搜索树；
DFS搜索会搜索全部，但是相比之下 DFS不用记录过多信息，所以搜素全部解的问题，DFS显然更加合适。