【算法修炼】动态规划专题三：游戏类、创新类题目

本文链接：https://blog.youkuaiyun.com/Mxeron/article/details/122756057

本博客继续总结DP题型，介绍了最小路径和、不同路径、不同路径Ⅱ、地下城游戏、过河马等问题。阐述了各题的状态转移方程和初始化要点，如最小路径和需比较左或上方网格大小；地下城游戏要从右下角遍历并考虑加血扣血情况等。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前面两个专题总结了大部分DP题型，本专题将会继续总结和介绍其它DP题型。

动态规划专题三

学习自：https://labuladong.gitee.io/algo/3/26/89/

1、最小路径和（中等）

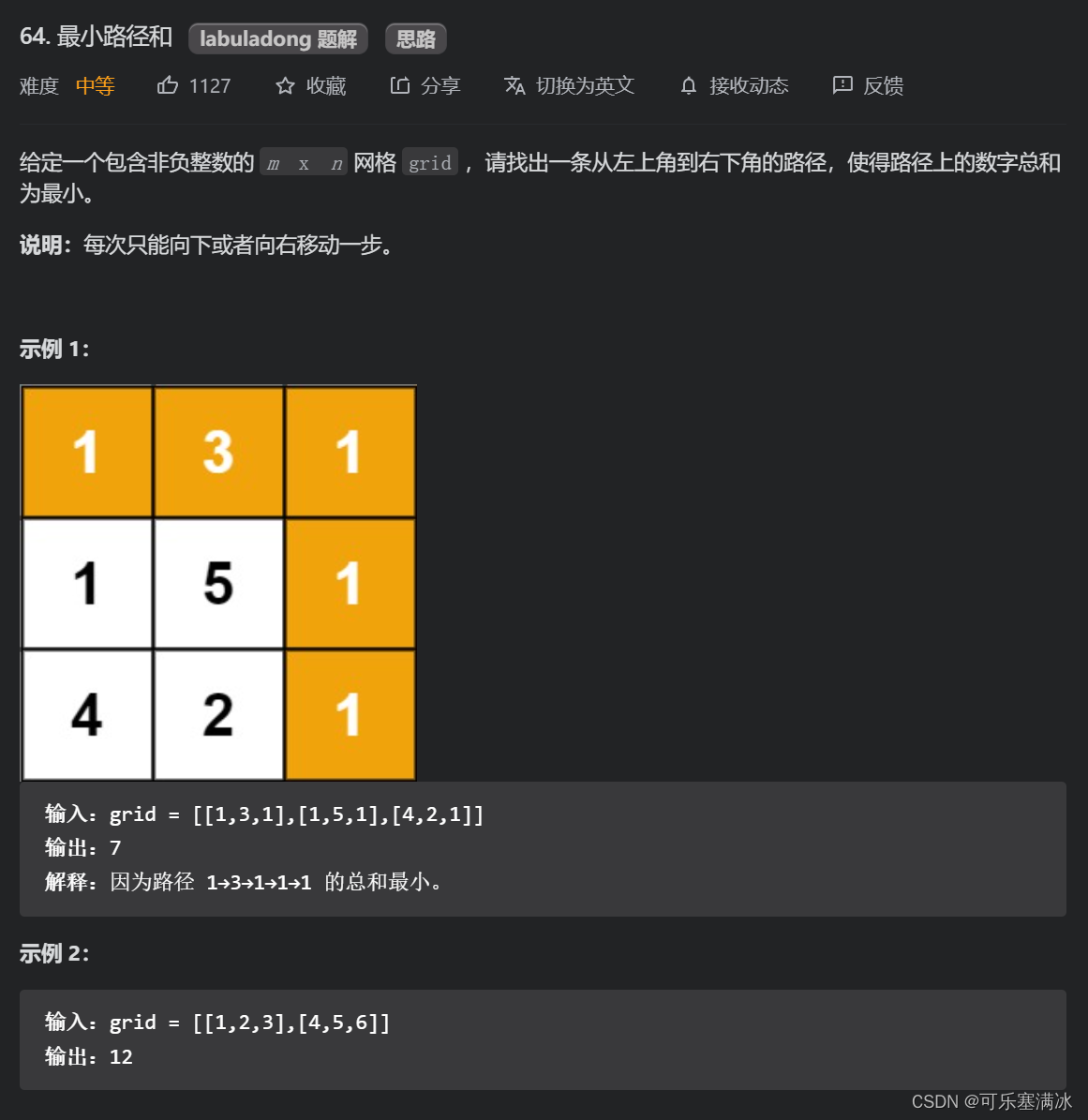
在这里插入图片描述
用dp[i][j]表示第i,j个网格的最小数字总和，如果以0为开始下标，那么最终答案就=dp[m-1][n-1]，题目的难点在于初始化，对于第一行所有元素，只能通过其左边元素右移一格得到；对于第一列所有元素，只能通过其上边元素下移一格得到，所以它们的值都是可以确定的。

状态转移方程：对于dp[i][j]，它可能由其左或上方的网格转移而来，所以只需要比较两者大小即可。dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j]

class Solution {
    public int minPathSum(int[][] grid) {
        // 每次只能向下、向右走一步
        int m = grid.length;
        int n = grid[0].length;
        int[][] dp = new int[m][n];
        // dp[i][j]:表示第i，j最小的数字总和
        dp[0][0] = grid[0][0];
        // 对于第0列的所有格子，只能通过一直往下走，所以它们的值是固定的
        for (int i = 1; i < m; i++) {
            dp[i][0] = dp[i - 1][0] + grid[i][0];
        }
        // 低于第0行的所有格子，只能通过一直往右走，所以它们的值是固定的
        for (int i = 1; i < n; i++) {
            dp[0][i] = dp[0][i - 1] + grid[0][i];
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
            }
        }
        return dp[m - 1][n - 1];
    }
}

2、不同路径（中等）

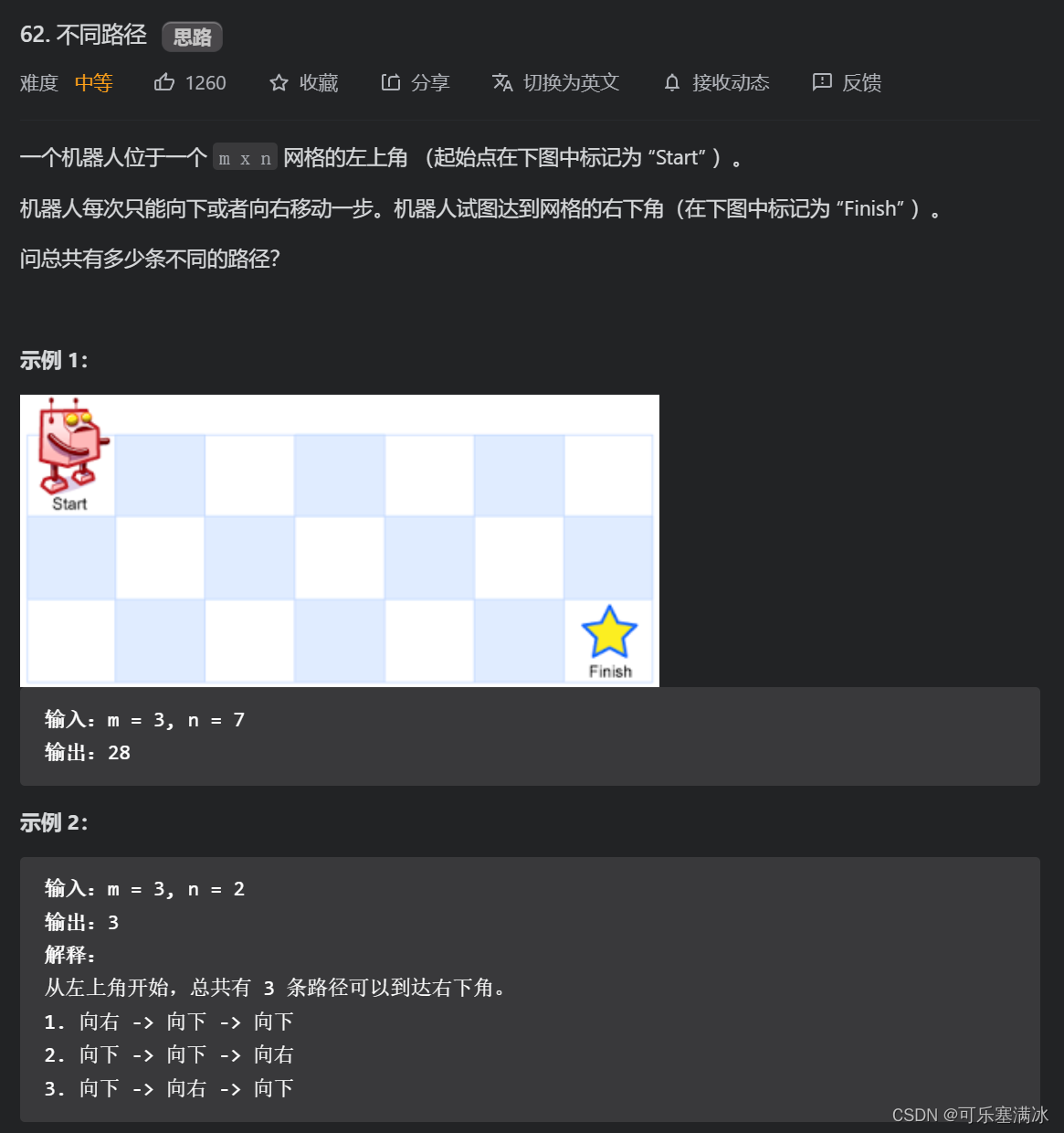
在这里插入图片描述
这道题和上一题一样，只不过一个求最值一个求方案数。

class Solution {
    public int uniquePaths(int m, int n) {
        // dp[i][j]：第i,j网格的路径数
        // 一个网格只可能由上方或左方移动而来：dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
        int[][] dp = new int[m][n];
        dp[0][0] = 1;
        // 对于第0列，到达的路径只有一条，由上方的网格往下走
        for (int i = 1; i < m; i++) {
            dp[i][0] = 1;
        }
        // 对于第0行，到达的路径只有一条，由左方的网格往右走
        for (int i = 1; i < n; i++) {
            dp[0][i] = 1;
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }
        return dp[m - 1][n - 1];
    }
}

3、不同路径Ⅱ（中等）

在这里插入图片描述
一样解法，对障碍物的地方特判一下，可能是当前网格的前面是障碍物，或者当前网格是障碍物。

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length;
        int n = obstacleGrid[0].length;
        int[][] dp = new int[m][n];
        if (obstacleGrid[0][0] == 0) {
            dp[0][0] = 1;
        }
        for (int i = 1; i < m; i++) {
            // 对于第0列而言，一旦上面有一个障碍或者本身就是障碍，那么下面或自己的地方一定无法到达
            if (obstacleGrid[i - 1][0] == 1 || obstacleGrid[i][0] == 1) {
                break;
            }
            dp[i][0] = 1;
        }
        for (int j = 1; j < n; j++) {
            if (obstacleGrid[0][j - 1] == 1 || obstacleGrid[0][j] == 1) {
                break;
            }
            dp[0][j] = 1;
        }
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (obstacleGrid[i][j] == 0) {
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
                }
            }
        }
        return dp[m - 1][n - 1];
    }
}

4、地下城游戏（困难）（路径升级版）

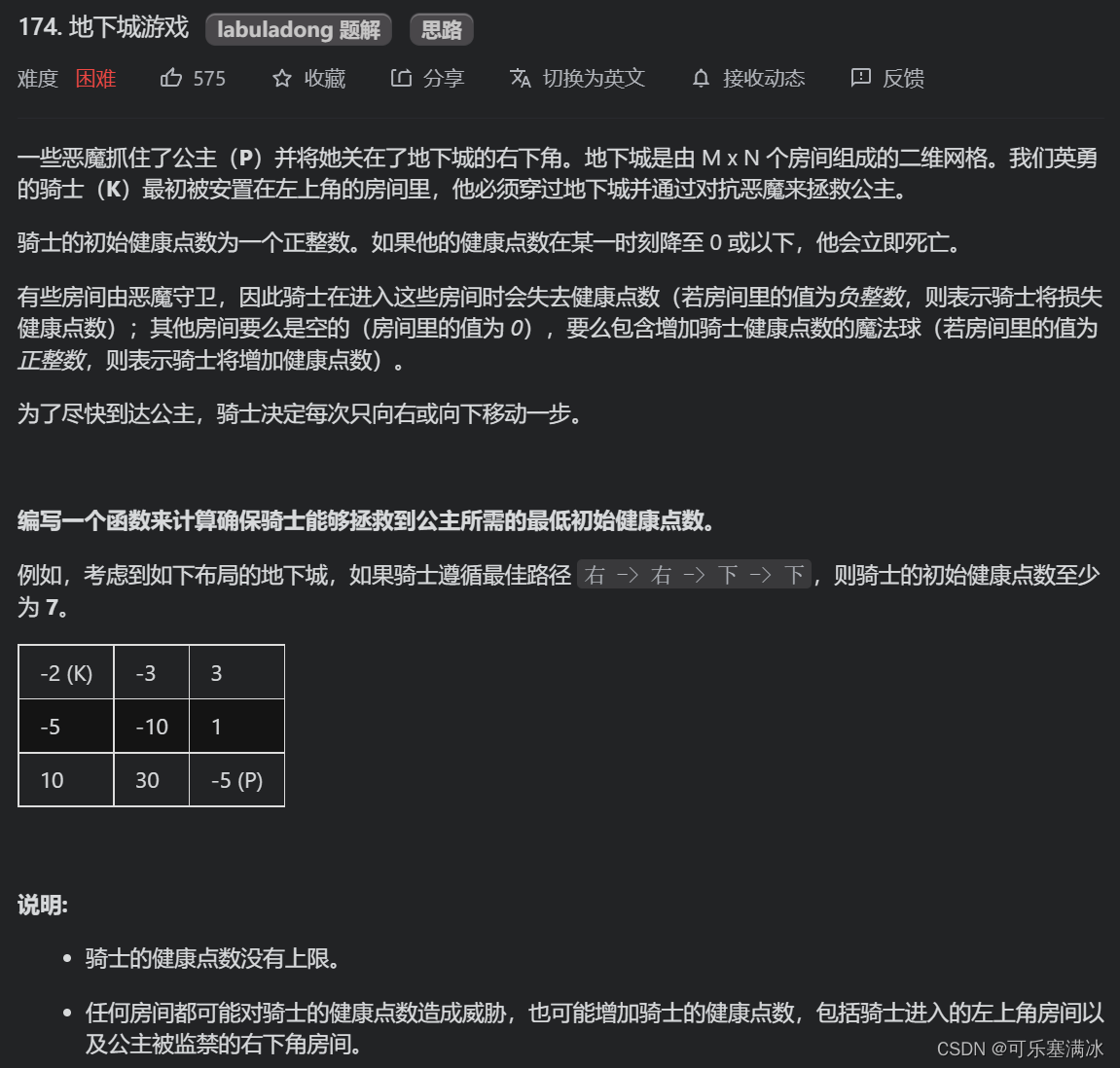
在这里插入图片描述
需要注意的是，此题必须从右下角开始遍历！

注意初始化的三种情况，如果是加血的，因为我们考虑的DP是第i,j网格所需的最少血量，因为它是加血的，那么只要保证到它这里的血量最少为1即可。如果是扣血的，那我们到达这里的血量至少要为1 + 扣血，这样扣掉血后最少剩1血。

状态定义：dp[i][j]表示从[i,j]到终点需要的最小血量，dp[0][0]就是最小初始血量
状态转移：
1. 如果dungeon[i][j] == 0，那么，dp[i][j] = min(dp[i+1][j], dp[i][j+1])
1. 如果dungeon[i][j] < 0，那么，dp[i][j] = min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j]
1. 如果dungeon[i][j] > 0，那么，dp[i][j] = max(1, min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j])
所以，三种情况可以统一成一种dp[i][j] = max(1, min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j])

需要注意的是，右下角的格子如果是加血珠，还是初始化为1，其它的格子遇到加血珠，要看之前转移过来的格子的血量，如果血量大于加血珠，那说明我们可以在这里加血后达到这个血量，所以更新为dp[i][j] - dungeon[i][jj]；如果血量不够减，小于加血珠，那说明到达加血珠的血量至少要为1。因为说明加了血之后，后面会遇到打怪的。

class Solution {
    public int calculateMinimumHP(int[][] dungeon) {
        // 每次只能向下、向右走一步
        int m = dungeon.length;
        int n = dungeon[0].length;
        int[][] dp = new int[m][n];
        // 必须从右下角往左上角遍历
        // 考虑右下角格子的情况：=0、<0、>0
        // 如果是小于零，那我们的血量至少为1 + 失去的血量
        // 如果是大于零，加血的，那血量至少还是1，注意我们只考虑最少需要血量
        dp[m - 1][n - 1] = Math.max(1, 1 - dungeon[m - 1][n - 1]);
        // 初始化最后一列
        for (int i = m - 2; i >= 0; i--) {
            // 如果遇到加血的，那就减去，但血量最低得为1，所以要看是否减为负数
            dp[i][n -1] = Math.max(1, dp[i + 1][n - 1] - dungeon[i][n - 1]);
        }
        for (int i = n - 2; i >= 0; i--) {
            dp[m - 1][i] = Math.max(1, dp[m - 1][i + 1] - dungeon[m - 1][i]);
        }
        // 状态定义：dp[i][j]表示从[i,j]到终点需要的最小血量，dp[0][0]就是最小初始血量
        // 状态转移：1. 如果dungeon[i][j] == 0，那么，dp[i][j] = min(dp[i+1][j], dp[i][j+1])
        //          2. 如果dungeon[i][j] < 0，那么，dp[i][j] = min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j]
        //          3. 如果dungeon[i][j] > 0，那么，dp[i][j] = max(1, min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j])
        // 所以，三种情况可以统一成一种dp[i][j] = max(1, min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j])
        for (int i = m - 2; i >= 0; i--) {
            for (int j = n - 2; j >= 0; j--) {
                if (dungeon[i][j] <= 0) {
                    dp[i][j] = Math.min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j];
                } else {
                    dp[i][j] = Math.max(1, Math.min(dp[i + 1][j], dp[i][j + 1]) - dungeon[i][j]);
                }
            }
        }
        return dp[0][0];
    }
}

5、过河马（中等）

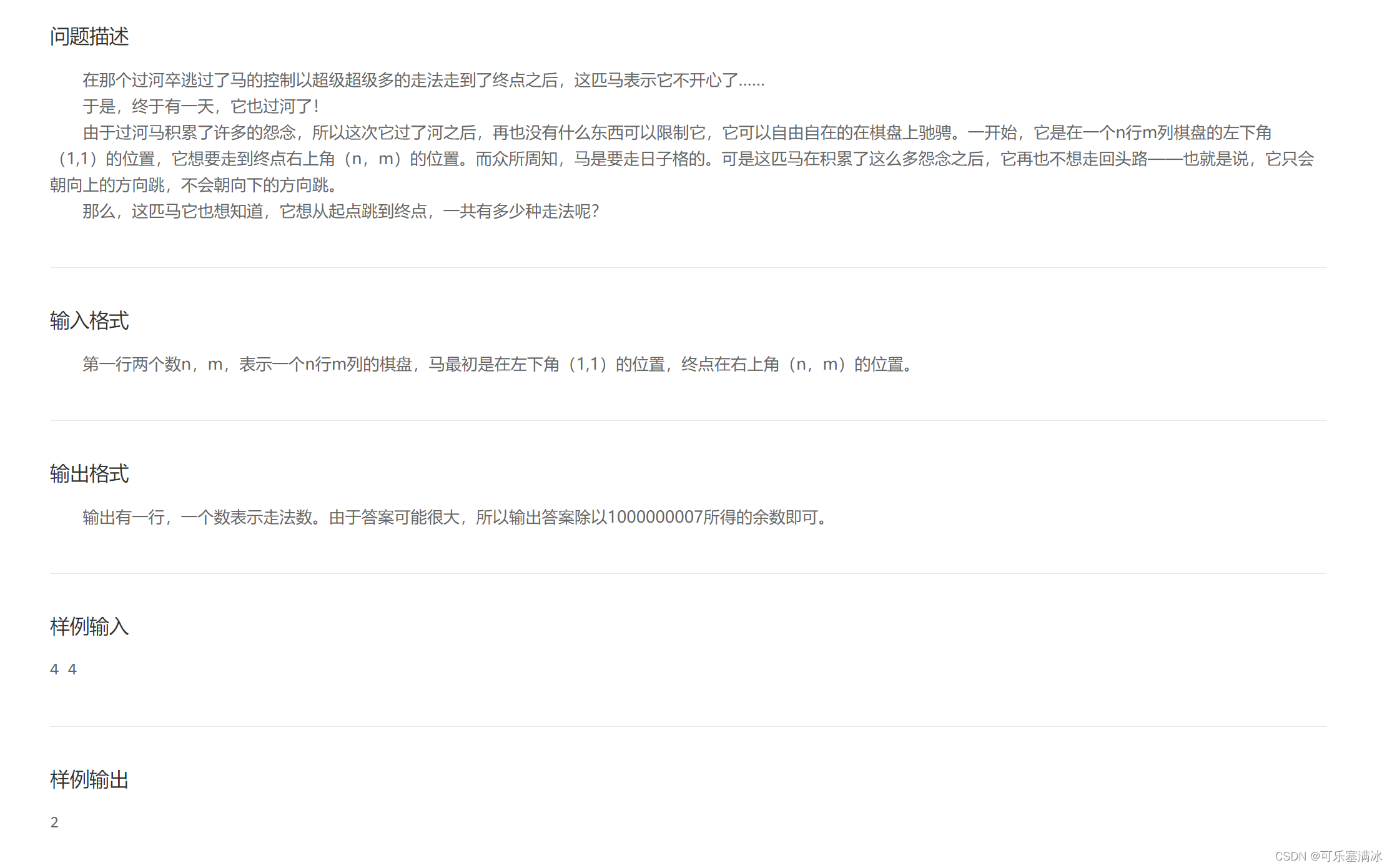
在这里插入图片描述
试试搜索？=》超时，看到数据量这么大，只能考虑dp了。

import java.util.*;

public class Main {
    static int n, m;
    static int[] xx = new int[] {1,1,2,2};
    static int[] yy = new int[] {2,-2,1,-1};
    static int[][] vis = new int[110][110];
    static int ans = 0;
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        n = scan.nextInt();
        m = scan.nextInt();
        vis[1][1] = 1;
        dfs(1, 1);
        System.out.println(ans);
    }
    static void dfs(int x, int y) {
        if (x == n && y == m) {
            ans = (ans + 1) % 1000000007;
            return;
        }
        for (int i = 0; i < 4; i++) {
            int tempx = x + xx[i];
            int tempy = y + yy[i];
            if (tempx < 1 || tempy < 1 || tempx > n || tempy > m || vis[tempx][tempy] == 1) {
                continue;
            }
            vis[tempx][tempy] = 1;
            dfs(tempx, tempy);
            vis[tempx][tempy] = 0;
        }
    }
}

dp做法，考虑马走的方向只能往上，所以一个点，它可以从四个点跳过来，所以要 = 四个方向之和。

import java.util.*;

public class Main {
    static int n, m;
    static int MOD = 1000000007;
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        n = scan.nextInt();
        m = scan.nextInt();
        int[][] dp = new int[n + 1][m + 1];
        // 从1,1出发，这两个点位都是确定的
        dp[3][2] = 1;
        dp[2][3] = 1;
        // 注意一定要从1,1开始，否则考虑不完全
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                if (i - 1 >= 1 && j - 2 >= 1) {
                    dp[i][j] = (dp[i][j] + dp[i - 1][j - 2]) % MOD;
                }
                if (i - 2 >= 1 && j - 1 >= 1) {
                    dp[i][j] = (dp[i][j] + dp[i - 2][j - 1]) % MOD;
                }
                if (i - 1 >= 1 && j + 2 <= m) {
                    dp[i][j] = (dp[i][j] + dp[i - 1][j + 2]) % MOD;
                }
                if (i - 2 >= 1 && j + 1 <= m) {
                    dp[i][j] = (dp[i][j] + dp[i - 2][j + 1]) % MOD;
                }
            }
        }
        System.out.println(dp[n][m]);
    }
}